無題

無題

KEN さんの書込 (2008/11/24(Mon) 16:26)

円柱座標のrotについて質問です． 円柱座標（r,θ,z）において，z軸方向の渦度をあらわす成分は rotの定義より（rot v＝∇×v）から計算すると ∂/r∂θ {v(r)}−∂/∂r {v(θ)} となったのですが，実際のテキストの記述を見ると ∂/r∂θ {v(r)}−∂/∂r {v(θ)}＋v(θ)/r となっていて，自分の計算ではv(θ)/rの項が出てきません． なぜでしょうか・・・． 回答お願いします．

Re: 無題

Yokkun さんのレス (2008/11/24(Mon) 17:36)

どのように計算されたのでしょうか？ 間違った計算の結果だけ示されてもわかりません．

Re: 無題

mNeji さんのレス (2008/11/24(Mon) 21:02)

ヴェクタの回転演算は直感的でないので泣かされますね．

この，物理かぎしっぽのJohさんが製作中の記事， ・h ttp://hooktail.maxwell.jp/kagi/9221aea3f0060a567695648c9fd6aca2.html は，とてもクールな解説だと思います．

この考え方を今回の問題に適応しますと，z軸に垂直な面内において，ヴェクタVを微小な線積分で一巡して，その微小面積で割ると，rot V]z になると言う事です．

実際に，z=一定のばあい，微小線積分回路ABCDA； 点A(ρ,φ)→点B(ρ+dρ,φ)→点C(ρ+dρ,φ+dφ)→点D(ρ,φ+dφ)→点A(ρ,φ) を計算して，その時の微小面積； dS = dρ・ρdφ で割れば，rot V]z が出ます．

このとき，dρやdφの1次までの近似とし，2次以上の微分は無視します．

また，点B→点Cの積分では，V_φ(ρ+dρ,φ,z)・(ρ+dρ)dφのようにρ依存性が入る事を忘れずに．同様に点D→点Aの積分では，V_φ(ρ,φ+dφ,z)・ρ(-dφ)です．

ここで，速度場を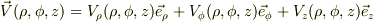， \vec V(\rho, \phi, z) =V_{\rho}(\rho, \phi, z)\vec e_{\rho} +V_{\phi}(\rho, \phi, z)\vec e_{\phi} +V_{z}(\rho, \phi, z)\vec e_{z} としたとき， V_φ(ρ,φ,z) := 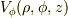V_{\phi}(\rho, \phi, z)

Re: 無題

toorisugari no Hiro さんのレス (2008/11/25(Tue) 10:59)

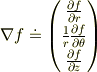
\nabla f &\doteq \begin{pmatrix}\frac{\partial f}{\partial r}\\\frac{1}{r}\frac{\partial f}{\partial \theta}\\\frac{\partial f}{\partial z}\end{pmatrix}

だからといって

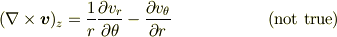
(\nabla\times\bm{v})_z &=\frac{1}{r}\frac{\partial v_r}{\partial \theta}-\frac{\partial v_\theta}{\partial r}\tag{not true}

にはなりません．(符号も違うように思うのですが，定義が違うのでしょうか?)

rotの計算においては，ベクトル成分だけでなく，基底ベクトルの変化の寄与も考慮に入れなければいけません．これを計算するにはストークスの定理を使うか，自然座標系を使うのが普通です．

2次元軸座標で

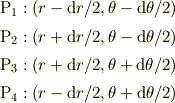
\mathrm{P}_1 &: (r - \mathrm{d}r/2, \theta - \mathrm{d}\theta/2)\\\mathrm{P}_2 &: (r + \mathrm{d}r/2, \theta - \mathrm{d}\theta/2)\\\mathrm{P}_3 &: (r + \mathrm{d}r/2, \theta + \mathrm{d}\theta/2)\\\mathrm{P}_4 &: (r - \mathrm{d}r/2, \theta + \mathrm{d}\theta/2)

となる4点を考えます．これらを結ぶ「長方形」上での線積分

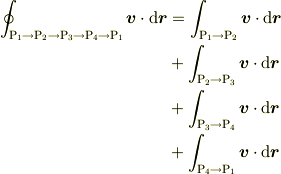
\oint_{\mathrm{P}_1\to\mathrm{P}_2\to\mathrm{P}_3\to\mathrm{P}_4\to\mathrm{P}_1}\bm{v}\cdot\mathrm{d}\bm{r}&= \int_{\mathrm{P}_1\to\mathrm{P}_2}\bm{v}\cdot\mathrm{d}\bm{r}\\&+ \int_{\mathrm{P}_2\to\mathrm{P}_3}\bm{v}\cdot\mathrm{d}\bm{r}\\&+ \int_{\mathrm{P}_3\to\mathrm{P}_4}\bm{v}\cdot\mathrm{d}\bm{r}\\&+ \int_{\mathrm{P}_4\to\mathrm{P}_1}\bm{v}\cdot\mathrm{d}\bm{r}

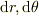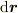を計算し，テーラー展開を \mathrm{d}r, \mathrm{d}\theta の一次の項まで実施してみてください．(ストークスの定理の証明と同じ手順です．) ( \mathrm{d}\bm{r} は長さの次元を持つことに注意してくださいね．ここがみそです．)

# あ，mNejiさんの解説とかぶってましたね．ごめんなさい．

Re: 無題

KEN さんのレス (2008/11/27(Thu) 20:46)

導出できました！ みなさんありがとうございますm(_ _)m

Re: 無題

toorisugari no Hiro さんのレス (2008/11/27(Thu) 23:02)

> みなさんありがとうございます

どう計算したか手順を書いてくださいな． 他の人の役に立つし，KENさんの次の質問も好感をもって迎えられるでしょう．