電磁気学の問題
電磁気学の問題
zephyr さんの書込 (2008/11/21(Fri) 09:00)
すみません,電磁気学の問題が解けないので助けて下さい. 「問題」 電気双曲子:微笑区間dで並ぶ点電荷qと-qの組.これはイオン結合性分子など分子の分極を表すモデルに使われる.双曲モーメント:p=qd dに比べて十分に遠方の点Pでの電位Φ(r)を求めなさい. ※答えは
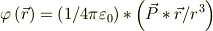
になるそうです.
次に電場を求めなさい. ※答えは
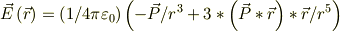
になるそうです.
以上です.お願いします.
Re: 電磁気学の問題
mNeji さんのレス (2008/11/21(Fri) 11:45)
zephyrさん,初めまして.
点電荷のクーロンの式はご存知ですね.例えば,原点の近くで,電荷+qが(x,y,z)=(0,0,+d/2)にあり,電荷-qが(x,y,z)=(0,0,-d/2)にある時に,ある点(x,y,z)でのポテンシャルは求められますよね.それぞれを加算すれば,求めるポテンシャルになります.
なお,電荷の双極子モーメントは,重心(質量モーメント)と同じで,
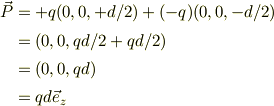
その後,x,y,zに比べて,dが十分に小さいとして近似できませんか?
Re: 電磁気学の問題
toorisugari no Hiro さんのレス (2008/11/21(Fri) 12:04)
以下の数学の問題に答えられますか? 1.
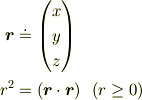
に対して,
(1)  を
を 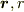 で表せ.
(2)
で表せ.
(2)  を
を 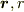 で表せ.
で表せ.
2. 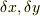 を微小量とする.
を微小量とする. 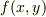 を無限回偏微分可能な関数として,
を無限回偏微分可能な関数として, 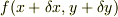 を
を 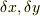 の1次式で近似せよ.
の1次式で近似せよ.
これに答えられるのなら,解を求める方法を紹介します.しかし,これが分からないなら,ゆっくりやるしかないですね.
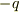 から
から 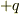 までのベクトルを
までのベクトルを 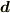 ,また
,また 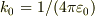 として,
として,