けいすけ さんの書込 (2008/11/17(Mon) 13:57)

拡散方程式を差分法で数値的に解く解きに疑問が生じたので質問させてください． 以下の図は，2Dの3x3のマス目です．真ん中の濃度が1でそれ以外を0とします．

000 010 000

この時，dC/dt = D*d^2C/dx^2の右辺を差分することで D/dx^2 * (C(x+1, y) + C(x-1, y) + C(x, y+1) + C(x, y-1) - 4C(x,y)) となります．上のマスの濃度を代入すると， D/dx^2 * (0+0+0+0 - 4) = -4D/dx^2 これが真ん中のマスのフラックスになります．

ここでdx -> dx/2, dy -> dy/2 として考え直すと，マスは 000000 000000 001100 001100 000000 000000 となります．この時中心濃度(4つの内どれも)のフラックスは D/(dx/2)^2 * (C(x+1, y) + C(x-1, y) + C(x, y+1) + C(x, y-1) - 4C(x,y)) = 4D/dx^2 * (0+0+1+1 - 4) = -8D/dx^2 となり，上の結果と異なり，拡散が早く進んでしまいます．

これを防ぐためには，一般的にはどのように対処されているのでしょうか？

よろしくお願いします．

toorisugari no Hiro さんのレス (2008/11/17(Mon) 16:44)

拡散方程式

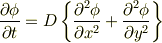
の差分化の問題ですか?

左辺が一階微分，右辺が2階微分ですから，バランスを考えて， 「空間刻みを半分にしたら時間刻みを4分の1(=半分^2)にする」 だけではないですか?

けいすけ さんのレス (2008/11/17(Mon) 21:00)

返信ありがとうございます．計算してみました． 前提は同じで，以下の2Dの3x3のマス目を濃度分布とします． 真ん中の濃度が1でそれ以外を0とします． 座標は左下を(1,1)とします． 000 010 000

拡散方程式を時間，空間ともに差分を取ります．時間に関しては前進差分をとります． dC/dt = D*d^2C/dt^2 (C(x,y,n+1)-C(x,y,n))/dt = D/dx^2*(C(x+1,y,n)+C(x-1,y,n)+C(x,y+1,n)+C(x,y-1,)-4C(x,y,n)) C(x,y,n+1) = C(x,y,n) + dt*D/dx^2*(C(x+1,y,n)+C(x-1,y,n)+C(x,y+1,n)+C(x,y-1,)-4C(x,y,n)) x,yに中心の座標を導入します． C(2,2,n+1) = C(2,2,n) + dt*D/dx^2*(C(3,2,n)+C(1,2,n)+C(2,3,n)+C(2,1,n)-4C(2,2,n)) C(2,2,n+1) = 1 + dt*D/dx^2*(0+0+0+0-4*1) C(2,2,n+1) = 1 + -4*dt*D/dx^2 (1)

次にご指摘の通り，dx->dx/2 dy->dy/2 dt->dt/4を導入します． 濃度分布は次のを考えます． 000000 000000 001100 001100 000000 000000

(C(x,y,n+1)-C(x,y,n))/(dt/4) = D/(dx/2)^2*(C(x+1,y,n)+C(x-1,y,n)+C(x,y+1,n)+C(x,y-1,)-4C(x,y,n)) C(x,y,n+1) = C(x,y,n)) + dt*D/dx^2*(C(x+1,y,n)+C(x-1,y,n)+C(x,y+1,n)+C(x,y-1,)-4C(x,y,n)) x,yに中心の座標((3,3),(3,4),(4,3),(4,4)どれも同じ結果です．)を導入します． C(3,3,n+1) = C(3,3,n) + dt*D/dx^2*(C(4,3,n)+C(2,3,n)+C(3,4,n)+C(3,2,n)-4C(3,3,n)) C(3,3,n+1) = 1 + dt*D/dx^2*(1+1+0+0-4*1) C(3,3,n+1) = 1 + -2*dt*D/dx^2 今，時間の刻みは1/4なので4step進めます． C(x,y,n+4) = 1 + -8*dt*D/dx^2 (2)

僕の計算間違いかわかりませんが，(1)式と(2)式の答えが異なってしまいます． どこを間違えているかわかりますでしょうか？

けいすけ さんのレス (2008/11/17(Mon) 21:17)

すいません．4step進めるところ間違いです． もう一回やりなおします．

けいすけ さんのレス (2008/11/18(Tue) 04:01)

すいません．手動だと複雑になりすぎて解けなかったんですが， 少なくとも拡散方程式を数値的に解く時に， dx->dx/2 dy->dy/2 としたら dt->dt/4 と変更しないと違う解が求まるということですか？

toorisugari no Hiro さんのレス (2008/11/18(Tue) 13:11)

> dx->dx/2 dy->dy/2 としたら dt->dt/4 と変更しないと違う解が求まるということですか？

差分「近似」ですから，有限の差分では，どのみち違う解です．ただ，精度が上がるか，計算が破綻するかという違いがあり得ます．

例えばポアッソン方程式

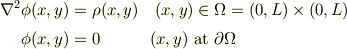
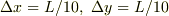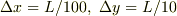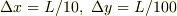を という刻みで差分近似するとします．これの結果の精度を良くしたいと思ったら刻みを小さくするのですが， とか でなく 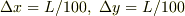などとするのがよいと誰でも思うでしょう．

バランスを崩して刻みを小さくしても，微分方程式の解に漸近していかないし，計算が破綻することもあり得ます．