積分

wing さんの書込 (2008/11/15(Sat) 20:47)

確率統計の問題で∫（積分区間-∞から∞）ｘ^2×e ^（-x ^2）dx＝π/2ってのがでてきたの

ですが詳しい式の展開がのってないものでなぜ答えがπ/2になるのかがわかりません．

自分で思いついたのは

部分積分で（積分区間は-∞から∞） x^2×∫e^（-x^2）-∫（x'）e^（-x^2）みたいになるかと思うのですが

この式ののxの部分に∞がはいってゼロになってしまいうまくいきません．

どうやって式を展開すればいいかわからず困っておりどなたかわかる方教えて

いただけないでしょうか？

右辺はπ/2ではなくて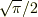， $\sqrt\pi/2$ だと思います．次のガウス積分の式はご存知でしょうか？

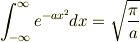
$\int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}$

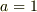両辺をで微分してから a=1 と置くと求める積分値が得られます．

失礼しました．

√π/2の間違いでした．

yamaさんの，パラメータ微分によるスマートな回答の後では蛇足ですが． x^2exp(-x^2)をx・xexp(-x^2)とみて，d/dx(e^(-x^2))=-2xexp(-x^2)に注意すれば，部分積分で簡単に出ます．但し，もちろん，∫exp(-x^2)dx=√πは既知としてですが．

回答ありがとうございます

ヒントを元に計算してみます