ラプラス方程式の解法について（具体例）

home > 掲示板 >

このページのPDF版

サイトマップ

ラプラス方程式の解法について（具体例）

ヒロさんの書込 (2008/11/15(Sat) 12:28)

大学１年で電磁気を習いたてです．演習を行っていたのですが，分かりませんでした．わかるかたよろしくお願いします．

TeX数式を使おうとしたのですが，実力不足でした．見にくくなりすいません．．．

問電荷のない半径aの導体球を考える．球の中心を原点とする．この空間全体に+z方向に大きさEの一様な電場をかける．

(1) 導体球のどこにどのような電荷が誘起され，空間の電場はどのようになるか，電荷の分布と電気力線の概形を図示せよ．

(2) このときの静電ポテンシャルをラプラス方程式を解いて求めよう．以下では，極座標で考える．静電ポテンシャルΦがr, θのみによるときは △Φ＝(r^-1)(∂^2(rΦ))/∂r^2) +(r^-2)((sinθ)^-1)∂(sinθ∂Φ/∂θ)/∂θ と書けることを示せ．

(3) Φ(r,θ)＝u(r)Θ(θ)/r とおくことで，ラプラス方程式は変数分離され２つの方程式となる．u(r)に関する方程式とΘ(θ)に関する方程式をそれぞれ導け．

(4) u(r)＝r^kとおくことで,u(r)の解としてどんなものがあるかを調べよ．

(5) 球から十分遠方では，一様電場のポテンシャル Φ＝-Ez＝-Ercosθ になっているはずである．そこで，Θ(θ)に関する方程式の特解の一つとしてΘ(θ)＝cosθがあるかどうかを調べよ．

(6) 球面上での境界条件Φ(a,θ)＝0と,球から十分遠方での境界条件Φ＝-Ercosθを満たすように,Φ(r,θ)を決定せよ．(この問題のΘ(θ)の解はcosθのみであるとまず仮定し,それによってu(r)の形を決定し，最後にこの形の解で境界条件を満たすようにできるならば，解の一意性によってそれがこの問題の解である．)

Re: ラプラス方程式の解法について（具体例）

mNeji さんのレス (2008/11/16(Sun) 11:02)

ヒロさん，初めまして．

問題としては，（１）が意外とし難ずかしく，他の問題は，計算力を試すものと思われます．

（１）に付いては，問題にもあるように遠方で電場が平行になることとに加えて，導体球に誘導される誘導電荷によった電場成分が加味されます．その変形した電場や，それが作る電気力線について考えて見ますと；

[i] 球の表面では，電場は球に垂直な成分しか持たない．言い換えると，球上の電位はz軸からの角度θに寄らず一定． [ii] (x,y,z)=(0,0,-∞)から出発した電場はz軸に沿って直進し，(x,y,z)=(0,0,-a) で球上の面電荷に吸収され，(x,y,z)=(0,0,+a)の点から面電荷から流れ出して，(x,y,z)=(0,0,+∞)に向けて直線的に進行する． [iii] (x,y)が球の断面より小さければ，電場は球に吸収され，z=0の面について対称的な点から再放出される． [iv] (x,y)が球の断面より大きければ，電場は|z|〜aで，球に向けて曲がるだけで遠方にいく． [v] (x,y)が球の断面より十分に大きければ，電場は球による吸収効果が発生せずに，もともとの平行電場のままに留まる．

と考えて見たらどうでしょうか．

他の問題は，お急ぎならば，他の方にヘルプをお出しください．

Re: ラプラス方程式の解法について（具体例）

なんとなくさんのレス (2008/11/16(Sun) 12:06)

横レス失礼します． mNejiさんのヒントはそれで良いのですが，もう少し，付け加えます． [i]具体的には導体表面（断面円）上では電気力線は”どこでも”半径方向，つまり円周に垂直な筈です．勿論円内に電気力線はありません．どうしてか考えてみましょう． [A]外部電場はｚ＝−∞→ｚ＝＋∞に向かう平行な電気力線とみなせますが，これはｚ＝−∞に＋１，ｚ＝＋∞に−１の電荷があると考えてもいいでしょう．そうすると，円中心より左側（中心を原点として−側）に−の電荷，右半分に＋の電荷が誘導されます． [B]電気力線は球対称性により，ｚ軸をはさんで線対称です． [C]電気力線同士は決して交わりません．以上のことを念頭において，ｚ軸を横倒しにして（Ｘ軸のように），左方から右方へ一定間隔の平行線を引き，どこかで円を書いて，その中の線分は消します．つぎに円周上に当たっている平行線端を円周に垂直に当たるよう曲げてつなぎ替えます．ｚ軸から遠ざかるほど大きく曲げられるはずです．円周外部でも円周にほど近い力線は大きく曲げられて円周上へ落ちます．さらに遠いものは曲げれても反対方向で逆に曲げられ，もとの平行線に合流するでしょう．さらに遠くは影響がほとんど無視できて，そのままです．これで，実は電気力線はその方向以外は左右も対称であることが分かります．くどいくらい書きましたが，イメージはわきましたか？

Re: ラプラス方程式の解法について（具体例）

ヒロさんのレス (2008/11/16(Sun) 13:57)

mNejiさん，なんとなくさん，はじめまして．返信ありがとうございます．非常に丁寧な回答で(1)について理解することができました．

（２）以降の問いについても私自身調べている最中ですが，どなたからか回答をいただけると幸いです．

引き続きよろしくお願いします．

Re: ラプラス方程式の解法について（具体例）

スパイクさんのレス (2008/11/16(Sun) 14:34)

こんにちは．

ラプラス方程式の典型的な解法だと思います．出題も丁寧な方だと思います．

まずは，設問を順繰りに解いていって，適宜参考書などを利用されてはいかがでしょう．

（1）状態の図示（説明図）

（2）ラプラス方程式の導出およびその確認

（3）ラプラス方程式に対する変数分離法の適用

（4）ラプラス方程式に対する動径方向の特性方程式の導出

（5）既知の解（境界条件）からの検算(もしくは，推定)

（6）境界条件より解を決定

＃以上，ご参考までですが．

*)習い立てだと，慣れるまでが大変かなと思いました．

Re: ラプラス方程式の解法について（具体例）

mNeji さんのレス (2008/11/16(Sun) 20:46)

(2)について

授業のなかで，どのような流れで直交座標系から極座標系に変換を説明されたかにもよりますが…．

私の推定では，(x,y,z)→(r,θ,φ)について講義で導出し，対称性から，φの依存性が無い場合の微分方程式を考えろ，といったものではありませんかね．

Re: ラプラス方程式の解法について（具体例）

スパイクさんのレス (2008/11/17(Mon) 00:06)

こんばんは．

取り敢えず，説明図は，大丈夫だそうですので，図を参考に計算過程を進めると以下のようになって来ると思います．

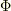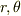静電ポテンシャル $\Phi$ が二変数 $r,\theta$ による時には，求める微分方程式は，

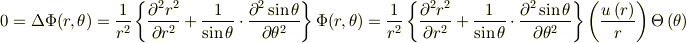
$0=\Delta \Phi (r,\theta )=\frac{1}{r^{2}}\left\{\frac{\partial ^{2}r^{2}}{\partial r^{2}}+\frac{1}{\sin \theta }\cdot \frac{\partial ^{2}\sin \theta }{\partial \theta ^{2}}\right\}\Phi (r,\theta )=\frac{1}{r^{2}}\left\{\frac{\partial ^{2}r^{2}}{\partial r^{2}}+\frac{1}{\sin \theta }\cdot \frac{\partial ^{2}\sin \theta }{\partial \theta ^{2}}\right\}\left(\frac{u\left(r\right)}{r}\right)\Theta \left(\theta \right)$

$\newline$

$=\frac{1}{r^{2}}\left[\frac{\,\mathrm{d}^{2}\left\{ru(r)\right\}}{\,\mathrm{d}r^{2}}\times \Theta \left(\theta \right)+\left\{\frac{u\left(r\right)}{r}\right\}\times \frac{1}{\sin \theta }\cdot \frac{\,\mathrm{d}^{2}\left\{\Theta \left(\theta \right)\sin \theta \right\}}{\,\mathrm{d}\theta ^{2}}\right]$

$\newline$

となります．従って，この二変数（動径・角度方向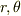； $r,\theta$ ）の変数分離を行うと $\alpha$ 定数として，

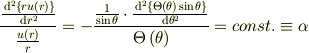
$\frac{\frac{\,\mathrm{d}^{2}\left\{ru(r)\right\}}{\,\mathrm{d}r^{2}}}{\frac{u\left(r\right)}{r}}=-\frac{\frac{1}{\sin \theta }\cdot \frac{\,\mathrm{d}^{2}\left\{\Theta \left(\theta \right)\sin \theta \right\}}{\,\mathrm{d}\theta ^{2}}}{\Theta \left(\theta \right)}=const.\equiv \alpha$

となり，二つの微分方程式が導かれます．そこで，動径方向の解を仮定してやるわけです．

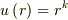
$u\left(r\right)=r^{k}$

これは，仮定解ですから，動径方向の微分方程式に代入してやると，いわゆる特性方程式が出て来ます．この場合には，についての二次方程式となります．即ち，

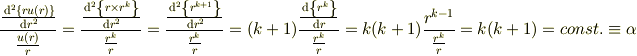
$\frac{\frac{\,\mathrm{d}^{2}\left\{ru(r)\right\}}{\,\mathrm{d}r^{2}}}{\frac{u\left(r\right)}{r}}=\frac{\frac{\,\mathrm{d}^{2}\left\{r\times r^{k}\right\}}{\,\mathrm{d}r^{2}}}{\frac{r^{k}}{r}}=\frac{\frac{\,\mathrm{d}^{2}\left\{r^{k+1}\right\}}{\,\mathrm{d}r^{2}}}{\frac{r^{k}}{r}}=(k+1)\frac{\frac{\,\mathrm{d}\left\{r^{k}\right\}}{\,\mathrm{d}r}}{\frac{r^{k}}{r}}=k(k+1)\frac{r^{k-1}}{\frac{r^{k}}{r}}=k(k+1)=const.\equiv \alpha$

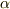後は，境界条件より，未定の定数と $\alpha$ を定めてやれば良いということなのです．

）概ねの手順という事と受け止めていただければ幸いかと存じ上げます． **）そうですが，本人が解いたことになるかどうかという点を重視したのですが．．．大学の課題ではなく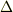？ **) $\Delta$ （第一式第三項）の表記に間違いがありました．正しくは，次の通りです（計算結果も違ってきます）． $\frac{1}{r^{2}}\left\{\frac{\partial ^{2}r^{2}}{\partial r^{2}}+\frac{1}{\sin \theta }\cdot \frac{\partial ^{2}\sin \theta }{\partial \theta ^{2}}\right\}\Phi (r,\theta )\rightarrow \frac{1}{r^{2}}\left\{r\frac{\partial ^{2}r\Phi (r,\theta )}{\partial r^{2}}+\frac{1}{\sin \theta }\cdot \frac{\partial \sin \theta \partial \Phi (r,\theta )}{\partial \theta ^{2}}\right\}$

Re: ラプラス方程式の解法について（具体例）

mNeji さんのレス (2008/11/17(Mon) 00:52)

スパイクさん，

そこまで書くとすると，角度に関する微分方程式に言及しないと片手落ちみたいに感じますけど．

Re: ラプラス方程式の解法について（具体例）

スパイクさんのレス (2008/11/17(Mon) 01:42)

それでは，mNejiさんのリクエストにお答えして；）

角度方向の微分方程式は，

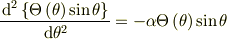
$\frac{\,\mathrm{d}^{2}\left\{\Theta \left(\theta \right)\sin \theta \right\}}{\,\mathrm{d}\theta ^{2}}=-\alpha \Theta \left(\theta \right)\sin \theta$

となっています．今，解が

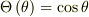
$\Theta \left(\theta \right)=\cos \theta$

となっているかどうか調べるため，角度方向の微分方程式に代入してみると，

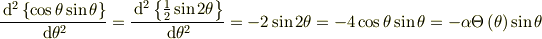
$\frac{\,\mathrm{d}^{2}\left\{\cos \theta \sin \theta \right\}}{\,\mathrm{d}\theta ^{2}}=\frac{\,\mathrm{d}^{2}\left\{\frac{1}{2}\sin 2\theta \right\}}{\,\mathrm{d}\theta ^{2}}=-2\sin 2\theta =-4\cos \theta \sin \theta =-\alpha \Theta \left(\theta \right)\sin \theta$

即ち，

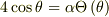
$4\cos \theta =\alpha \Theta \left(\theta \right)$

となる為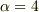， $\alpha =4$ のとき，

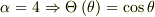
$\alpha =4 \Rightarrow \Theta \left(\theta \right)=\cos \theta$

と言えますので，確かに，角度方向の微分方程式は，

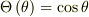
$\Theta \left(\theta \right)=\cos \theta$

を解に持つことが分かります．

*）ここまでは，宜しいでしょうか？

Re: ラプラス方程式の解法について（具体例）

ミュフ猫さんのレス (2008/11/17(Mon) 04:24)

皆さん，こんばんは．

静電ポテンシャルΦ(r,θ)が，変数分離形の解をもつという仮定はどこから来るんですか？つまり，互いに独立な二関数U(r)/r，Θ(θ)の積で表せるって仮定の根拠は何ですか？

Re: ラプラス方程式の解法について（具体例）

スパイクさんのレス (2008/11/17(Mon) 05:16)

おはよう御座います．

一言で言うと，私は簡潔さだと思います．

実際の自然の（非線形の）現象を線形近似することにより，数学的に取り扱いやすくする手法と見たほうがいいかもしれません．（その為に説明図を描かせたのかどうかは，定かではありませんが．．．）変数分離については，独立因子とみなすことにより，線形近似していると見た方が，自然だとは思います．利点：簡潔に記述できることが多い欠点：自然さが損なわれることが多い＃ご参考までですが．

*）誤解があるようです．二次の微少量が無視されています．

Re: ラプラス方程式の解法について（具体例）

mNeji さんのレス (2008/11/17(Mon) 08:51)

スパイクさんのNo.22197に関してコメントします．

変数分離法と，固有値・固有関数の関係が大事な状況だとおもいます．その一部に焦点を当てて，細かな説明を積み重ねると，初学者の方は，読むに連れて疑問が深まってしまう可能性が高いと思います．

勿論，私は数学が苦手な為に誤解をしているかも知れません．物理の問題の場合，物理的解釈については，多角的に検討することは初心者にとっても大切だとおもいます．しかし，数学的な方法論については，平明にして，バランス良く説明するのが望まれるのではないでしょうか？

また，No.22199の＞変数分離については，独立因子とみなすことにより，線形近似している＞と見た方が，自然だとは思います．

私は，変数分離法が線形近似をしているとは，知りませんでした．仮に，そうだとしても，この問題の解説に必要なのでしょうか？

Re: ラプラス方程式の解法について（具体例）

toorisugari no Hiro さんのレス (2008/11/17(Mon) 15:10)

> 変数分離法と，固有値・固有関数の関係が大事な状況だとおもいます．

そうだと思います．もともと線形のシステムですから，「線形近似」は存在しません．

線形の世界では重ね合わせの原理が使えます．任意の解を基本モードの線形和の形にできます．

基本モードはある演算子の固有関数に取るのが自然です．

ラプラス演算子を 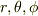$r,\theta,\phi$ 微分，それぞれに対して分解し，それぞれの演算子の固有関数の積を基本モードとしたもの考えているのが，今回の変数分離法です．

Re: ラプラス方程式の解法について（具体例）

yama さんのレス (2008/11/17(Mon) 17:02)

非線形方程式の場合でも，変数分離によって線形近似されるわけではないでしょう．むしろ，線形近似せずに非線形のままで方程式を解くために変数分離をするのだと思います．たとえば，中心対称な重力場の方程式を変数分離してシュバルツシルト解を得る場合などです．非線形の場合は，重ね合わせの原理が成り立たず，固有値や固有関数が存在しないので，変数分離の位置づけは線形の場合とは違ってきます．

本問の場合は線形なので，mNejiさんやtoorisugari no Hiroさんの説明に沿って理解されるのがいいでしょう．

Re: ラプラス方程式の解法について（具体例）

mNeji さんのレス (2008/11/17(Mon) 21:08)

■現在製作中．

(3)について，異論が在るので具体的に話を進めてみます．しかし，前提となる(2)が不明確なままだと困るので，そこから始めます．

電荷の無い空間では，静電ポテンシャルはラプラスの方程式の解です．この方程式は，2階の線形同次偏微分方程式です．

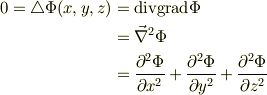
$0 = \triangle \Phi (x,y,z)&= \mathrm{div }\mathrm{grad}\Phi \\&= \vec \nabla ^2 \Phi \\&= \frac{\partial^2 \Phi}{\partial x^2} +\frac{\partial^2 \Phi}{\partial y^2} +\frac{\partial^2 \Phi}{\partial z^2}$

$(x,y,z) \to (r,\theta, \phi)$ と座標変換すると，長〜い計算の結果，

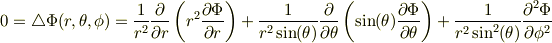
$0 = \triangle \Phi(r,\theta, \phi) = \frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2\frac{\partial \Phi}{\partial r}\right)+\frac{1}{r^2 \sin(\theta)}\frac{\partial}{\partial \theta }\left ( \sin(\theta) \frac{\partial \Phi}{\partial \theta} \right) +\frac{1}{r^2 \sin^2(\theta)} \frac{\partial^2 \Phi}{\partial \phi^2}$

となります．これだけ複雑でも，依然として線形微分方程式です．

ここで，系がz軸について回転対象であれば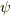， $\psi$ の項は無く成るので，

$0 = \triangle \Phi(r,\theta) = \frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2\frac{\partial \Phi}{\partial r}\right)+\frac{1}{r^2 \sin(\theta)}\frac{\partial}{\partial \theta }\left ( \sin(\theta) \frac{\partial \Phi}{\partial \theta} \right) ---[1]$

いよいよ (3)に突入します．

ただし，書き易さの為に，次の様な表示を取ります；

$\Phi(r,\theta) =\frac{R(r)}{r}A(\theta) ---[2]$

そこで，式[1]に式[2]を代入して，辺々を 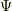$\Psi$ で割ると；

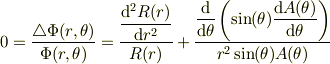
$0 =\frac{ \triangle \Phi(r,\theta)}{\Phi(r,\theta)} &=\frac{\dfrac{\mathrm{d}^2 R(r)}{\mathrm{d} r^2}}{R(r) } +\frac{\dfrac{\mathrm{d}}{\mathrm{d} \theta }\left ( \sin(\theta) \dfrac{\mathrm{d} A(\theta)}{\mathrm{d} \theta} \right)}{r^2 \sin(\theta)A(\theta)}$

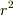上の式に r^2 を掛けると，その右辺の第1項はだけの関数，第2項は $\theta$ だけの関数となる．よって，各項は符号が違うだけの定数 $\lambda$ に等しい；

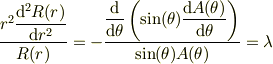
$\frac{r^2 \dfrac{\mathrm{d}^2 R(r)}{\mathrm{d} r^2}}{R(r) } =-\frac{\dfrac{\mathrm{d}}{\mathrm{d} \theta }\left ( \sin(\theta) \dfrac{\mathrm{d} A(\theta)}{\mathrm{d} \theta} \right)}{ \sin(\theta)A(\theta)} = \lambda$

これは，次の連立微分方程式と考える事も出来る；

$\dfrac{\mathrm{d}^2 R(r)}{\mathrm{d} r^2} &=\lambda r^{-2}R(r) ---[3]\\\dfrac{\mathrm{d}}{\mathrm{d} \theta }\left ( \sin(\theta) \dfrac{\mathrm{d} A(\theta)}{\mathrm{d} \theta} \right) &=-\lambda \sin(\theta)A(\theta) ---[4]$

以上で(3)の導出は終わります．式[4]の微分方程式をジックリ後確認下さい．

また，重要なのは，上の連立方程式を得る事で，定数 $\lambda$ とそれに対応する解が決まる事です．この時の定数を固有値，関数を固有関数と言います．一般的にこれを求めるには，数学的な準備が必要です．

が，この問題では，(4)で示される様に，式[4]の特解を 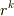r^k と仮定した時のkに関する特性方程式，(5)に示された遠方解r・cos(θ)を式[4]に適用して，逆に固有値方程式を出させる方針だろうと思います．

ここまでで疑問はありますか？

Re: ラプラス方程式の解法について（具体例）

ヒロさんのレス (2008/11/17(Mon) 21:48)

返事が遅くなり申し訳ありません．非常に丁寧な回答で助かっています．ありがとうございます．

(2)までは，mNejiさんのNo.22207を参考に，調べたところ途中経過を含め理解することができました．

(3)以降について私の理解しているとことです．．．

まず，(2)では三次元の極座標におけるラプラシアンを導出し，導出した式のΦ依存項をおとし，スパイクさんのNo.22193のアドバイスどおりに式をいじくり，微分方程式を解き，(4)でk(k-1)＝αの関係を得る．(5)でさらにスパイクさんのアドバイスよりα＝４となる．最後の(6)で二つの境界条件を満たすようなｋを求める．（kが存在すればそれが解の一意性によって答えとなる．)（存在しなければΘ(θ)＝(4cosθ)/αとおいて(6)の境界条件二つよりαとkを解く・・・？）

といった具合で進めればよいのではないかと思うのですが．．．まだ(6)でkを求めるやり方を考えている最中です．

Re: ラプラス方程式の解法について（具体例）

ミュフ猫さんのレス (2008/11/17(Mon) 22:40)

スパイクさん

ご返事ありがとうございました．

Re: ラプラス方程式の解法について（具体例）

mNeji さんのレス (2008/11/17(Mon) 22:51)

ヒロさん，

＞(5)でさらにスパイクさんのアドバイスよりα＝４となる．

今日，通院中に概算をしてみていたのですが，この値には疑問を持ちます．というのも(5)の遠方での解は，「r^1」に比例するので，少なくとも「k=2」が解の一つでないとなりませんが，そうすると，k(k-1)=2*(2-1)=2となって矛盾します．

それでスパイクさんとは別に計算を準備中(No.22207)です．最近，こちらの数式を使っていないのでトラブル続きですが...，しばしお待ちを．

Re: ラプラス方程式の解法について（具体例）

スパイクさんのレス (2008/11/17(Mon) 22:52)

こんばんは．

ヒロさんへ．

>まず，(2)では三次元の極座標におけるラプラシアンを導出し，導出した式のΦ依存項をおとし， >スパイクさんのNo.22193のアドバイスどおりに式をいじくり，微分方程式を解き，(4)でk(k-1)＝αの関係を得る． >(5)でさらにスパイクさんのアドバイスよりα＝４となる．最後の(6)で二つの境界条件を満たすようなｋを求める． >（kが存在すればそれが解の一意性によって答えとなる．)（存在しなければΘ(θ)＝(4cosθ)/αとおいて >(6)の境界条件二つよりαとkを解く・・・？）

定量的（解析的）には，そのような手順で構わないかと思われます．（細かい点や数値につきましては，必要があれば，適宜御修正下さい）＃ご理解頂き有難う御座います．

定性的には，mNejiさんの意見が参考になるかと思われます．＃線形性の解釈に行き違いがあったようですね．

ミュフ猫さんへ．

どう致しまして．舌足らずな点がございましたら，ご容赦下さい．＃この手は，気をつけないと，どうしても二次の微少量が絡んでくるですよね．

）結果として，正答に繋がれば宜しいかと思われます． *)下記の議論で，正答に辿り着くかと思われます．ホッとしました．

Re: ラプラス方程式の解法について（具体例）

yama さんのレス (2008/11/18(Tue) 00:31)

１つのkの値だけで境界条件を満たすことはできず，異なるkの値を持つ項の重ね合わせを考える必要があるでしょう．

そう思って電磁気学の本を調べてみたところ，同じ問題が扱われており，解は次のようになるそうです．

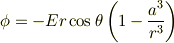
$\phi=-Er\cos\theta\left(1-\frac{a^3}{r^3}\right)$

これは，外部電場と，球面上の電荷による電場の重ね合わせになっていて，後者は双極子モーメントによる電場と同じですね．

Re: ラプラス方程式の解法について（具体例）

mNeji さんのレス (2008/11/18(Tue) 01:02)

（４）と（５）について．

No.22207で述べた次の連立方程式； $\dfrac{\mathrm{d}^2 R(r)}{\mathrm{d} r^2} &=\lambda r^{-2}R(r) ---[3]\\ \dfrac{\mathrm{d}}{\mathrm{d} \theta }\left ( \sin(\theta) \dfrac{\mathrm{d} A(\theta)}{\mathrm{d} \theta} \right) &=-\lambda \sin(\theta)A(\theta) ---[4]$

をベースに検討します．

式[3]に特解として 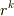r^k を仮定すると，kの特性方程式は，

$k(k-1)=\lambda ---[3a]$

遠方解は，

$\Psi &\sim -Ez\\&= -Er\cos(\theta) ---[5]$

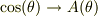だから，式[4]で， $\cos(\theta) \to A(\theta)$ と仮定してみると

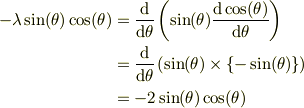
$-\lambda \sin(\theta)\cos(\theta) &=\dfrac{\mathrm{d}}{\mathrm{d} \theta }\left ( \sin(\theta) \dfrac{\mathrm{d} \cos(\theta)}{\mathrm{d} \theta} \right) \\&=\dfrac{\mathrm{d}}{\mathrm{d} \theta }\left( \sin(\theta) \times \{-\sin(\theta)\} \right)\\&=-2\sin(\theta)\cos(\theta)$

故に，固有値は，

$\lambda = 2 ---[4a]$

これより特性方程式[3a]は，

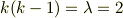
$k(k-1)=\lambda =2$

この解は，

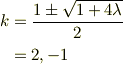
$k &= \frac{1 \pm \sqrt{1 +4\lambda}}{2}\\&= 2, -1$

となる．丁寧に言えば，固有値 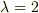$\lambda =2$ に属するR(r)の固有関数は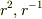， $r^2, r^{-1}$ の二つの関数になる．

従って，一般解は特解(固有関数)の線形和で与えられるから，定数B,Cとして，

$\Psi =\frac{Br^2 +Cr^{-1}}{r}\cos(\theta) ---[6]$

定数Bを決めるには 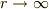$r \to \infty$ で遠方解[5]，無限遠方の境界条件，になることから決まります．常数Cは，球体の表面(r=a)で角度依存性が消える事から決まると思います．

〜〜〜〜 No.22213でyamaさんが，「後者は双極子モーメントによる電場と同じですね．」と仰っています．式[6]から電場を求めると金属表面の静電誘導電荷密度を求める事，ひいては，双極子モーメントも計算出来ますね．

そういう意味では，おそらく，鏡像法でも解けますね．だとすると， No.22188で，なんとなくさんが遠方電場を点電荷に置き換える提案をされていたのが，ようやく分ったような気がします．

何れの方法をとるにしても，ラプラスの方程式は物理の色々な場面ででてきます．toorisugari no Hiroさんや yamaさんがコメントされているように，この方程式は線形偏微分方程式です．その一般的な固有関数は厳密に解けています．物理数学で特殊関数を学ぶまでお待ち下さい．

Re: ラプラス方程式の解法について（具体例）

toorisugari no Hiro さんのレス (2008/11/18(Tue) 17:55)

(3)以下についてはmNejiさんがわかりやすい解説をされたので， > $(x,y,z) \to (r,\theta, \phi)$ と座標変換すると，長〜い計算の結果，

(2)について説明します．いろいろ，やり方はあるでしょうが，グリーンの定理(もどき)を使うのが簡単と思います．

今，曲線直交座標系 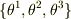$\{\theta^1,\theta^2,\theta^3\}$ を考えます．変位ベクトルとナブラ，及び体積要素は，

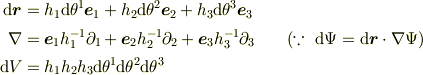
$\mathrm{d}\bm{r}&= h_{1} \mathrm{d}\theta^1\bm{e}_1+ h_{2} \mathrm{d}\theta^2\bm{e}_2+ h_{3} \mathrm{d}\theta^3\bm{e}_3\\\nabla &= \bm{e}_1 h_{1}^{-1} \partial_1+ \bm{e}_2 h_{2}^{-1} \partial_2+ \bm{e}_3 h_{3}^{-1} \partial_3\qquad (\because~ \mathrm{d}\Psi=\mathrm{d}\bm{r}\cdot\nabla\Psi)\\\mathrm{d}V&= h_{1}h_{2}h_{3} \mathrm{d}\theta^1 \mathrm{d}\theta^2 \mathrm{d}\theta^3$

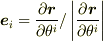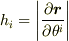と書けます．(ただし， $\bm{e}_{i}=\frac{\partial \bm{r}}{\partial \theta^i}/ \left|\frac{\partial \bm{r}}{\partial \theta^i}\right|$ , $h_{i}=\left|\frac{\partial \bm{r}}{\partial \theta^i}\right|$ )

ベクトル解析の公式

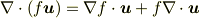
$\nabla\cdot(f \bm{u}) &= \nabla f \cdot \bm{u} + f \nabla\cdot\bm{u}$

を既知とすると，

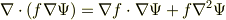
$\nabla\cdot(f \nabla \Psi) &= \nabla f \cdot \nabla \Psi + f \nabla^2 \Psi$

が得られるので，を境界で消える任意関数として，ガウスの発散定理により，

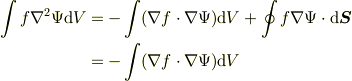
$\int f \nabla^2 \Psi \mathrm{d}V &= - \int (\nabla f \cdot \nabla\Psi) \mathrm{d}V + \oint f \nabla \Psi \cdot \mathrm{d}\bm{S}\\&= - \int (\nabla f \cdot \nabla\Psi) \mathrm{d}V$

(グリーンの定理もどき)が得られます． # これをラプラシアンの定義と考えても良いです．

右辺を成分で計算し，(境界積分は0として)部分積分を行えば，左辺の成分表示が得られます．は任意関数ですから，これより，ラプラシアンの成分表示が得られます．

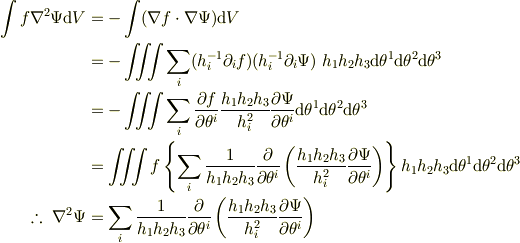
$\int f \nabla^2 \Psi \mathrm{d}V&= -\int (\nabla f \cdot \nabla\Psi) \mathrm{d}V\\&= -\iiint \sum_{i} (h_i^{-1}\partial_i f) (h_i^{-1}\partial_i \Psi) ~h_1h_2h_3 \mathrm{d}\theta^1 \mathrm{d}\theta^2 \mathrm{d}\theta^3\\&= -\iiint \sum_{i} \frac{\partial f}{\partial\theta^i}\frac{h_1h_2h_3}{h_i^2}\frac{\partial\Psi}{\partial\theta^i}\mathrm{d}\theta^1 \mathrm{d}\theta^2 \mathrm{d}\theta^3\\&= \iiint f \left\{\sum_{i} \frac{1}{h_1h_2h_3} \frac{\partial}{\partial\theta^i} \left( \frac{h_1h_2h_3}{h_i^{2}} \frac{\partial\Psi}{\partial\theta^i}\right)\right\} h_1h_2h_3 \mathrm{d}\theta^1 \mathrm{d}\theta^2 \mathrm{d}\theta^3\\\therefore ~\nabla^2 \Psi &= \sum_{i}\frac{1}{h_1h_2h_3}\frac{\partial}{\partial\theta^i} \left(\frac{h_1h_2h_3}{h_i^{2}}\frac{\partial\Psi}{\partial\theta^i} \right)$

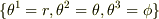極座標 $\{\theta^1=r,\theta^2=\theta,\theta^3=\phi\}$ の場合，

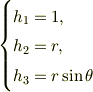
$\begin{cases}h_1 = 1,\\ h_2 = r,\\ h_3 = r\sin\theta\end{cases}$

ですから

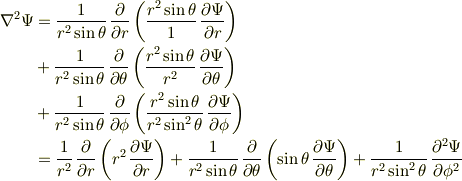
$\nabla^2 \Psi &= \frac{1}{r^2\sin\theta}\,\frac{\partial}{\partial r} \left(\frac{r^2\sin\theta}{1}\,\frac{\partial\Psi}{\partial r}\right)\\&+ \frac{1}{r^2\sin\theta}\,\frac{\partial}{\partial \theta} \left(\frac{r^2\sin\theta}{r^2}\,\frac{\partial\Psi}{\partial \theta}\right)\\&+ \frac{1}{r^2\sin\theta}\,\frac{\partial}{\partial \phi} \left(\frac{r^2\sin\theta}{r^2\sin^2\theta}\,\frac{\partial\Psi}{\partial \phi}\right)\\&=\frac{1}{r^2}\,\frac{\partial}{\partial r}\left( r^2\,\frac{\partial \Psi}{\partial r}\right)+\frac{1}{r^2 \sin\theta}\,\frac{\partial}{\partial \theta }\left ( \sin\theta \,\frac{\partial \Psi}{\partial \theta} \right)+\frac{1}{r^2 \sin^2\theta} \,\frac{\partial^2 \Psi}{\partial \phi^2}$

が得られます．

Re: ラプラス方程式の解法について（具体例）

ヒロさんのレス (2008/11/18(Tue) 23:52)

みなさん返事が遅くなりすいません．非常に多くの返信があり感謝しています．

mNejiさん,スパイクさんはじめ皆さんのレスのおかげで最後まで解ききることができました．ありがとうございます．

最後のtoorisugari no Hiroさんのグリーンの定理を使って極座標のラプラシアンを導出するやり方はもう少し自分で考えてみます．非常に手短に計算できてそうでしたので．．．

明日大学の図書館にでも行ってみます．

[home] [掲示板] [ページの先頭]