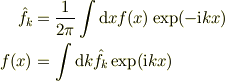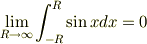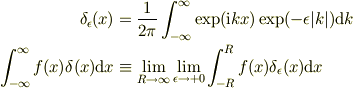おちえて

home > 掲示板 >

このページのPDF版

サイトマップ

おちえて

トビラ．．さんの書込 (2008/11/12(Wed) 20:21)

ディラックのデルタ関数のフーリエ変換がよくわからないのですが，フーリエ変換を

$F(\omega)=\Im[f(x)] =\int^\infty_{-\infty}f(x)e^{-i\omega x}dx$

としてフーリエ逆変換を

$f(x)=\Im^{-1}[F(\omega)]=\frac{1}{2\pi}\int^\infty_{-\infty}F(\omega)e^{i\omega x}d\omega$

とします．すると，デルタ関数のフーリエ変換は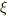（ $\xi$ を定数，を変数として）

$\Im[\delta(\xi-x)]=\int^\infty_{-\infty}\delta(\xi-x)e^{-i\omega(\xi-x)}dx=1$

となるから

$\delta(\xi-x)=\Im^{-1}[1]=\frac{1}{2\pi}\int^\infty_{-\infty}e^{i\omega(\xi-x)}d\omega$

となりますよね？でも，僕が読んでいる本ではデルタ関数のフーリエ変換は

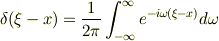
$\delta(\xi-x)=\frac{1}{2\pi}\int^\infty_{-\infty} e^{-i\omega (\xi-x)}d\omega$

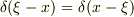となってての指数の符号が反対なんです．デルタ関数の対称性 $\delta(\xi-x)=\delta(x-\xi)$ から符号が反対でも大丈夫かなと思ったんですけども，それだと

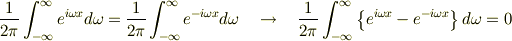
$\frac{1}{2\pi}\int^\infty_{-\infty}e^{i\omega x}d\omega=\frac{1}{2\pi}\int^\infty_{-\infty}e^{-i\omega x}d\omega\quad\to\quad\frac{1}{2\pi}\int^\infty_{-\infty}\left\{e^{i\omega x}-e^{-i\omega x}\right\}d\omega=0$

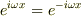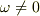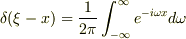とならなくてはいけないから $e^{i\omega x}=e^{-i\omega x}$ となって $\omega\not =0$ で矛盾すると思うんです．自由空間での波動方程式のグリーン関数を勉強していたら， $\delta(\xi-x)=\frac{1}{2\pi}\int^\infty_{-\infty}e^{-i\omega x}d\omega$ が成り立たないとダメなんですけど，どうなんでしょうか？どちらのデルタ関数のフーリエ変換が正しいのですか？

Re: おちえて

toorisugari no Hiro さんのレス (2008/11/12(Wed) 20:23)

フーリエ変換の定義の問題．私は

$\hat f_k &= \frac{1}{2\pi} \int \mathrm{d}x f(x) \exp(-\mathrm{i} k x)\\f(x) &= \int \mathrm{d}k \hat f_k \exp(\mathrm{i} k x)$

という定義をよく使います．

Re: おちえて

トビラ．．さんのレス (2008/11/12(Wed) 20:26)

え？定義を任意に反対にして大丈夫なんですか？あと，デルタ関数の対称性からこの二つのフーリエ変換はイコールにならないのでしょうか？疑問符ばかりで申し訳ないです．

Re: おちえて

toorisugari no Hiro さんのレス (2008/11/12(Wed) 20:34)

> デルタ関数の対称性からこの二つのフーリエ変換はイコールにならないのでしょうか？

> え？定義を任意に反対にして大丈夫なんですか？

首尾一貫していれば．

Re: おちえて

トビラ．．さんのレス (2008/11/12(Wed) 20:38)

え，もしかして 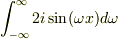$\int^\infty_{-\infty}2i\sin(\omega x)d\omega$ って収束して０になるんですか？勉強不足でした，即答ありがとうございました．（すごいなやんだのに）

Re: おちえて

toorisugari no Hiro さんのレス (2008/11/12(Wed) 20:39)

> え，もしかして $\int^\infty_{-\infty}2i\sin(\omega x)d\omega$ って収束して０になるんですか？

奇関数の積分

Re: おちえて

トビラ．．さんのレス (2008/11/12(Wed) 20:42)

なるほど，奇関数だから 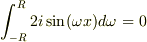$\int^R_{-R}2i\sin(\omega x)d\omega=0$ ですね．(ガーン) またお世話になりました．どうもありがとうございました．

Re: おちえて

toorisugari no Hiro さんのレス (2008/11/12(Wed) 20:54)

> なるほど，奇関数だから 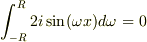$\int^R_{-R}2i\sin(\omega x)d\omega=0$ ですね．

厳密なこと言うと 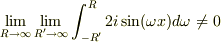$\lim_{R\to\infty}\lim_{R'\to\infty}\int^R_{-R'}2i\sin(\omega x)d\omega \ne 0$ なんだけど，デルタ関数は積分の中でしか意味を持たないからそこ辺は目を瞑る．

Re: おちえて

トビラ．．さんのレス (2008/11/12(Wed) 21:11)

ああなるほど，同じ無限でも無限＝無限とならないからですよね．でも

$\lim\limits_{R\to \infty}\int^R_{-R}\sin xd x=0$

は厳密になりたちますよね？

Re: おちえて

toorisugari no Hiro さんのレス (2008/11/12(Wed) 21:21)

> 厳密になりたちますよね

もち．

実際は

$\delta_{\epsilon}(x) &= \frac{1}{2\pi} \int_{-\infty}^{\infty} \exp(\mathrm{i}kx)\exp(-\epsilon |k|) \mathrm{d}k\\\int_{-\infty}^{\infty}f(x) \delta(x) \mathrm{d}x &\equiv \lim_{R\to\infty}\lim_{\epsilon\to +0}\int_{-R}^{R}f(x) \delta_\epsilon(x) \mathrm{d}x$

とか定義するから問題ないですね．

Re: おちえて

トビラ．．さんのレス (2008/11/12(Wed) 21:44)

ふむふむ，無限で積分しても実際本当に積分しているのはほぼ０に近い有限領域だけだからですね．（たぶん） toorisugari no hiroさんはどこかの大学の教授ですか？数学力めちゃんこすごいですけども

Re: おちえて

toorisugari no Hiro さんのレス (2008/11/12(Wed) 21:57)

そういうことは聞かないのが大人のたしなみ．

Re: おちえて

トビラ．．さんのレス (2008/11/12(Wed) 22:04)

僕知能は子供なんで・・・つい，（シークレットということで）今日もありがとうございました．

[home] [掲示板] [ページの先頭]