初歩だと思うんですが，謎です

ですから，具体的に偏微分操作をすれば公式を導けませんか？でも，数学の得意な方はスマートな方法を取るし，普通の人は面倒ですから自分で計算しないとおもうので，バカ正直な計算をお目にかけましょう． <pre> rot C]x = ∂y(AxBy - AyBx) -∂z(AzBx - AxBz) = ∂y(Ax)By + Ax∂y(By) -∂y(Ay)Bx - Ay∂(Bx) -[ ∂z(Az)Bx + Az∂z(Bx) - ∂z(Ax)Bz - Ax∂z(Bz) ] = { By∂y + Bz∂z}(Ax) - { Ay∂y + Az∂z}(Bx) +Ax{ ∂y(By) + ∂z(Bz)} - Bx{ ∂y(Ay) + ∂z(Az)}

● ■ ↓+Bx∂x(Ax) ↓-Ax∂x(Bx) = { By∂y + Bz∂z}(Ax) - { Ay∂y + Az∂z}(Bx) +Ax{ ∂y(By) + ∂z(Bz)} - Bx{ ∂y(Ay) + ∂z(Az)} ↑+Ax∂x(Bx) ↑-Bx∂x(Ax)

■ ●

= {Bx∂x + By∂y + Bz∂z}(Ax) -{ Ax∂x + Ay∂y + Az∂z}(Bx) +Ax{ +∂x(Bx) + ∂y(By) + ∂z(Bz)} - Bx{ +∂x(Ax) + ∂y(Ay) + ∂z(Az)} = {B・∇}(Ax) - {A・∇}(Bx) +Ax{∇・B} - Bx{∇・A} </pre> 従って， <pre> rot A×B = {B・∇}A - {A・∇}B + A{∇・B} - B{∇・A} = A{∇・B} - B{∇・A} + {B・∇}A - {A・∇}B = A div B - B div A + {B・∇}A - {A・∇}B </pre>

終わり．

Re: 初歩だと思うんですが，謎です

toorisugari no Hiro さんのレス (2008/11/10(Mon) 11:23)

横から失礼します．

> ベクトルの基本演算の問題です．
> ∇×(A×B)=(∇・B)A−(∇・A)B

=(∇・B)A+(∇・B)A−(∇・A)B＋(∇・A)B

これは基本演算ではありません．

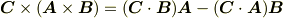
$\bm{C}\times(\bm{A}\times\bm{B}) &= (\bm{C}\cdot\bm{B})\bm{A}-(\bm{C}\cdot\bm{A})\bm{B}$

は「ベクトル3重積」と呼ばれる基本演算でベクトルの名が付くどんな教科書にも書いてありますが，上の式はベクトル微分演算子 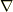$\nabla$ を含んでいますので「ベクトル3重積」をそのままでは適用できません．しかし，「積の微分」の規則( 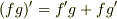(fg)'=f'g+fg' )を考慮すると以下のように適用する事ができます．

ハット 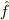$\hat f$ のついた項に微分が作用するとします．

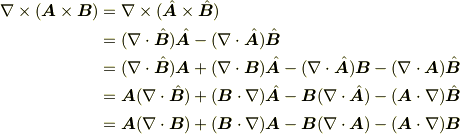
$\nabla\times( \bm{A} \times \bm{B} )&= \nabla\times( \hat{\bm{A}} \times \hat{\bm{B}} ) \\&= (\nabla\cdot \hat{\bm{B}} ) \hat{\bm{A}}- (\nabla\cdot \hat{\bm{A}} ) \hat{\bm{B}}\\&= (\nabla\cdot \hat{\bm{B}} ) \bm{A} + (\nabla\cdot \bm{B} ) \hat{\bm{A}}- (\nabla\cdot \hat{\bm{A}} ) \bm{B}- (\nabla\cdot \bm{A} ) \hat{\bm{B}}\\&= \bm{A} (\nabla\cdot \hat{\bm{B}} ) + (\bm{B}\cdot \nabla) \hat{\bm{A}}- \bm{B}(\nabla\cdot \hat{\bm{A}} ) - (\bm{A}\cdot\nabla) \hat{\bm{B}}\\&= \bm{A} (\nabla\cdot \bm{B} ) + (\bm{B}\cdot \nabla) \bm{A}- \bm{B}(\nabla\cdot \bm{A} ) - (\bm{A}\cdot\nabla) \bm{B}$

となります．(第3式が積の微分です．また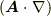， $(\bm{A}\cdot\nabla)$ はスカラー微分演算子です．)

先生はこのつもりで書かれたのではないでしょうか？

Re: 初歩だと思うんですが，謎です

nbtr さんのレス (2008/11/12(Wed) 00:39)

mNejiさん＞＞お返事ありがとうございます！！ナルホド……馬鹿正直にするとめちゃくちゃしんどいですね(T□T) スマートなやり方とは，どんな方法化できれば教えていただきたいです！！

toorisugari no Hiroさん＞＞あぁぁ積の導関数ですか！！俺はかなり頭悪い方なんで，よくわからないところがあるんですが，まず第4式から第5式に行くときのように，ハットは勝手に取ってもいんですか？？

Re: 初歩だと思うんですが，謎です

toorisugari no Hiro さんのレス (2008/11/12(Wed) 11:42)

> まず第4式から第5式に行くときのように，ハットは勝手に取ってもいんですか？？

スカラー関数に対する（＝普通の)「積の微分」で考えてみましょう．

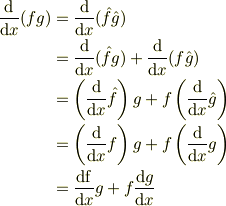
$\frac{\mathrm{d}}{\mathrm{d}x}(fg) &= \frac{\mathrm{d}}{\mathrm{d}x}(\hat f \hat g)\\ &= \frac{\mathrm{d}}{\mathrm{d}x}(\hat f g)+ \frac{\mathrm{d}}{\mathrm{d}x}(f \hat g)\\ &= \left(\frac{\mathrm{d}}{\mathrm{d}x}\hat f \right) g+ f \left(\frac{\mathrm{d}}{\mathrm{d}x} \hat g \right)\\ &= \left(\frac{\mathrm{d}}{\mathrm{d}x} f \right) g+ f \left(\frac{\mathrm{d}}{\mathrm{d}x} g \right)\\ &= \frac{\mathrm{df}}{\mathrm{d}x} g+ f \frac{\mathrm{d}g}{\mathrm{d}x}$

ハットがついている間は，スカラー微分演算子はただのスカラーと同じように積の交換則(順番の変更)や結合則(括弧の付け替え)がつかえます．「積の微分」則をつかい，順番や括弧付けを適切なものにして，ハットをはずしても微分がどの項に作用にしているのか明確になったら，ハットを取ってかまいません．

ベクトル演算子も，ハットがついている間はただのベクトルとして扱える，という意味で同じです．

> スマートなやり方とは，どんな方法化できれば教えていただきたいです！！

最初から「スマートなやり方」に飛びついても，まちがって理解するだけです．是非，一度mNejiさんの計算を自分でやってみてください．それを経験しないと「スマートなやり方」のありがたみが理解できません．

Re: 初歩だと思うんですが，謎です

mNeji さんのレス (2008/11/12(Wed) 12:38)

＞ナルホド……馬鹿正直にするとめちゃくちゃしんどいですね(T□T)

そうです，直感的に判り易くしようとすると面倒くさい事を避けられない場合があります．特に，物理では，その対象の理解が大切なので，数学的な構造が奇麗か，汚いかは，別問題だと思っています．

ヴェクタの外積や，ヴェクタの回転演算(rot,∇×)は，系の回転に関係した現象の記述と密接に関係するので一度くらいは，手計算しても宜しいかと感じます．

＞スマートなやり方とは，どんな方法化できれば教えていただきたいです！！

∇は，基底ヴェクタと微分演算子とからなる「奇妙な」ヴェクタなので，演算関係が複雑に成る訳です．

解析力学の講義などで，微分形式の項で，外積の一般化を学ばれると思いますが，現時点で解説できません．

Re: 初歩だと思うんですが，謎です

nbtr さんのレス (2008/11/12(Wed) 14:14)

toorisugari no Hiroさん＞＞ナルホド理解しました♪ 一応mNejiさんのやり方で，計算してみましたが，しんどさがかなりわかりました．．

mNejiさん＞＞今日教授の説明を聞いたら，∇は『演算子』だから∇の右側にあるものにだけ微分操作を行うという説明でした．説明でも∇はかなり奇妙なものだといっていました．．

お二人ともありがとうございました！！

[home] [掲示板] [ページの先頭]