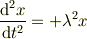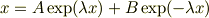微分方程式
微分方程式
う〜ん さんの書込 (2008/11/10(Mon) 00:16)
教科書の問題で d^{2}x/dt^2=-kx というのを解かなければならない問題があったのですがわからず,解説をみたら, これを解くとx=Acos√{k/m}t+Bsin√{k/m}t (A,Bは任意定数) としか書かれていなくて,どうやって解いて上のx=の式になったのかがまったくわからないのです.どなたか教えていただけませんでしょうか?
Re: 微分方程式
snow さんのレス (2008/11/10(Mon) 02:16)
の関係を使えばうまくいくはずです.
Re: 微分方程式
う〜ん さんのレス (2008/11/11(Tue) 01:54)
すみませんわかりません.高校で導入程度しかやっていないのですが大学では普通に使われるので困っているところなのです.教えてもらえますか?また易しい文献などあればご紹介してくださればうれしいです.
Re: 微分方程式
mNeji さんのレス (2008/11/11(Tue) 03:18)
横から失礼します.
三角関数の微分を思い出すと
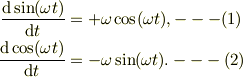
そこでもう一度時間で微分すると,
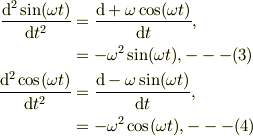
となります.このように正弦関数,余弦関数は二回微分すると定数項  の自乗が掛かるものの,自分自身と等しくなる性質があります.
の自乗が掛かるものの,自分自身と等しくなる性質があります.
また,正弦関数,余弦関数とは同じ時間の値で比較すると決して一致しません.相互に独立な関数です.
ですから, 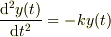 のタイプの微分方程式を見ると,正弦関数,余弦関数の和で一般的に解けると思って良いのです.
のタイプの微分方程式を見ると,正弦関数,余弦関数の和で一般的に解けると思って良いのです.
Re: 微分方程式
toorisugari no Hiro さんのレス (2008/11/11(Tue) 11:44)
> 高校で導入程度しかやっていないのですが大学では普通に使われるので困っているところなのです.
これは「微分を知らない」(つまり,指数関数の微分や三角関数の微分や対数関数の微分をよく理解していない.オイラーの公式もテーラー展開も知らない)と思っていいのでしょうか?
もし,そうなら,今回の問題は手に余ります.たぶん,説明も最初からやらなければいけないので無理でしょう.
微分積分を最初からきちんと理解される事をお勧めします.
「(やさしい)微分積分入門」等と名が付いた教科書や参考書を購入されて,「さっと読んで暗記する」勉強法でなく,「一つ一つ概念を手で解いて確かめて,納得いくまで考え方を身にしみこませる」やり方で勉強をされないと,現状では厳しいと思います.
とりあえず,中身は見てないので保証はできませんが,以下の本から始められてはどうでしょう.
イラスト・図解 はじめての微分積分―考え方から学べて,好きになる微積入門
図解雑学 わかる微分・積分(絶版だが入手可能)
図解雑学 三角関数
図解雑学 指数・対数
今回の微分方程式(単振動の運動方程式)は,今後も使われる重要な事項ですが,その気になれば半年で全くの初心者が完全にマスターできる程度の概念です.勉強していけば,数ヶ月でそれなりに効果が見えてきます.あきらめずに手を抜かずに地道にがんばってください.
Re: 微分方程式
う〜ん さんのレス (2008/11/13(Thu) 17:49)
ヒロさんありがとうございます,参考に勉強させていただきます.私は理系科目が苦手だったにもかかわらずなぜか理系にいて,得意だった文系科目で点をとって受かったようなもので,概念的なものはほぼわかっていないのです.これから頑張りますね.
う〜ん,mNejiさんのいっていることは,両辺ともにt関数yがあるから微分して自身と関数的に同形になる三角関数使えばよい,尚正,余弦が相互に独立だから和によってすべての値をとれる,ということでよいのでしょうか??わかりにくくて申し訳ないです・・あとこれが正しいなら三角関数とeの累乗はそれぞれどう使い分けるのでしょうか?関数的な同形性からいうならばどちらをつかってもよいということになりませんか?
・・・・・すみません,ちょっと疑問に思ったので最後の質問しましたが勉強した後でしろって感じですよね,教えてくれたらありがたいです..
Re: 微分方程式
mNeji さんのレス (2008/11/14(Fri) 00:54)
私は,数学が苦手なので,大雑把な感触を書いて見ます.敢えて,三角関数だけに絞って話を進めます.
>尚正,余弦が相互に独立だから和によってすべての値をとれる
いまご質問の微分方程式は,整理すると,
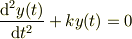
となります.y(t)やその微分成分の1次式の和で構成される微分方程式,線形微分方程式であり,ある解があれば,それに係数を掛けた解もこの微分方程式の解になるので,線形同次微分方程式と呼ばれます.同次というのは,右辺がゼロであり,外力がないような場合に対応します.
線形同次微分方程式のばあい,その任意の解(一般解)には,一番高階な微分の次数;nとする;だけの未知定数が許されます.いまの場合,n=2ですから,2個の定数が出て来ます.
#物理の微分方程式では,未知定数というよりは,初期条件と言った方がしっくりするかも知れませんね.
また,n階の線形同次微分方程式には,n個の独立な解がある事が知られています.従って,n=2の場合,正弦関数と余弦関数は解であるのですから,一般解は
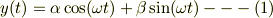
と書く事が可能です.
積分定数, 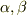 は,初期条件,
は,初期条件, 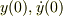 を与えれば,決まりますね.
を与えれば,決まりますね.
>関数的な同形性からいうならばどちらをつかってもよいということになりませんか?
三角関数の範疇で説明します.例えば,新たな2つの定数,
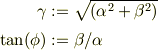
を考えると,式(1)は,三角関数の積和公式から,
![y(t) &= \gamma \cdot [\cos(\phi)\cos(\omega t) +\sin(\phi)\sin(\omega t)]\\&= \gamma \cos(\omega t -\phi) ---(2)](http://hooktail.maxwell.jp/bbslog/0269639eb821ce7d18cebad10a14e8e9.png)
と変形可能です.勿論,正弦関数に変換するのも容易ですよね.
その意味では,一つの正弦関数なり余弦関数と,2つの定数,振幅 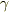 と位相角
と位相角  とで一般解を表せる,とも言えます.
とで一般解を表せる,とも言えます.
Re: 微分方程式
toorisugari no Hiro さんのレス (2008/11/14(Fri) 01:07)
最後のご質問は,,,,意味が分かりません.ごめんなさい.
> これから頑張りますね.
「微分方程式 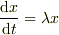 の一般解は
の一般解は 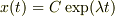 である.」
である.」
という文章の意味が分かり,これを自分の手で導出できたら,8合目です.これを目標にがんばってください.
# テーラー展開とオイラーの公式は6,7合目かな.