テンソル
テンソル
ファイル さんの書込 (2008/11/06(Thu) 20:24)
物理科の大学四年生です. 数学のことは殆ど詳しくないのですが,物理の特定の分野に出てくるテンソルについての疑問があります.質問させてください.
力学に出てくるテンソルは,たとえば,
慣性テンソル
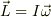 (Lは角運動量,ωは角速度です.)などのように
向きの違うベクトル同士を結びつける量,つまりは
ベクトルをベクトルに変換するような量,という意味だと思います.
応力テンソルなども,これに分類されるものと思います.
(Lは角運動量,ωは角速度です.)などのように
向きの違うベクトル同士を結びつける量,つまりは
ベクトルをベクトルに変換するような量,という意味だと思います.
応力テンソルなども,これに分類されるものと思います.
一方,相対論に出てくるテンソルは
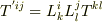 などのように,変換行列L(あるいはその逆行列)によって,変換されるものとして定義されていると思います.
座標変換によってどのように変換されるか,ということから,様々な物理量がこのテンソルとして記述されます.
などのように,変換行列L(あるいはその逆行列)によって,変換されるものとして定義されていると思います.
座標変換によってどのように変換されるか,ということから,様々な物理量がこのテンソルとして記述されます.
前者は変換するもの,後者は変換されるもの,というふうに全く逆の立場であり 物理的にも,前者は明確であるのに対して,後者はかなり抽象的ですが これは数学的には別の種類のテンソルなのでしょうか? 的外れの質問でしたら,すみません. 私の考えでは,後者のほうがテンソルの定義で,前者は二階テンソルの具体的な応用例?のようなものだと思っているのですが・・・.
Re: テンソル
toorisugari no Hiro さんのレス (2008/11/06(Thu) 21:46)
> 前者は変換するもの,後者は変換されるもの,というふうに全く逆の立場であり
変換という言葉を乱用しています. 同じ場所に定義された異なるベクトルの間の線形関係を記述する量と 同じ物理量の異なる座標系で定義された成分を結ぶ関係とは 違うものです.
前者は観測者の状態に関係しない純粋な「物理量」ですが,後者は同じ物理量を異なる観測者が定量化したとき,それぞれのデータの間の「読み替え規則」です.
(混合)テンソルと座標変換を混同してはいけません.
Re: テンソル
ファイル さんのレス (2008/11/06(Thu) 22:56)
>前者は観測者の状態に関係しない純粋な「物理量」ですが,後者は同じ物理量を>異なる観測者が定量化したとき,それぞれのデータの間の「読み替え規則」です.
そうですね.そのへんの理解が曖昧でした. ということは,前者と後者では言葉で上手く言えませんが,なんか全く違うもののような気がしますね・・・. それなのに,同じテンソル?ですか.
この場合,数学的には同一のテンソルを,物理的に違う使い方をしている,と考えるべきでしょうか. それとも,数学的にも別の種類のテンソルと考えるべきなのでしょうか? そもそもテンソルとは何か?という部分が分かっていないのかもしれません.
>(混合)テンソルと座標変換を混同してはいけません. これはどういうことでしょうか?
追記 テンソルとは何かが分かっていないと書きましたが 教科書などをみると,後者の,「正則行列によって座標変換されるもの」をテンソルとして定義しています. どちらかというと,よく分からないのは前者のほうです.
Re: テンソル
toorisugari no Hiro さんのレス (2008/11/06(Thu) 23:11)
> それなのに,同じテンソル?ですか.
そもそもベクトルだって
- 大きさと方向と向きを持つ量
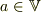 ,
, 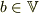 ,
, 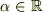 then
then 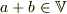 ,
, 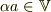 となる集合
となる集合 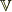 の元
の元- 二つの異なる座標系X,X'において
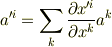
と変換される数字の組 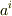 (を成分とする量)
(を成分とする量)
といった一見異なる定義があるじゃないですか?(一般性の高さとか違う部分もありますが...)
> そもそもテンソルとは何か?という部分が分かっていないのかもしれません.
もし,「ベクトルも分かっていないのでは?」と思われたならそうかもしれません.
# 双対ベクトルってご存じですか?
>> (混合)テンソルと座標変換を混同してはいけません. > これはどういうことでしょうか?
ファイルさんが「変換」という言葉であらわされたものは,上のように全く違う名前のついた,全く違う概念だということです.
> どちらかというと,よく分からないのは前者のほうです.
テンソルも二つの定義があります.
「座標変換で 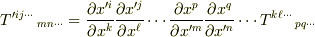 と変換する数の組(を成分とする量)」がテンソルであると定義するものと,
「ベクトル(や双対ベクトル)を引き数とし,スカラー値を返す(多変数)線形関数」がテンソルであるという定義です.
と変換する数の組(を成分とする量)」がテンソルであると定義するものと,
「ベクトル(や双対ベクトル)を引き数とし,スカラー値を返す(多変数)線形関数」がテンソルであるという定義です.
数学では後者が主流で,私もこの定義の方が,抽象的だが,本質が見えるのですきです.
Re: テンソル
yama さんのレス (2008/11/07(Fri) 16:49)
一般的な説明はtoorisugari no Hiroさんが述べられている通りですが,2階のテンソルをデカルト座標で記述する場合について説明しておきます.
たとえば,慣性テンソル 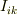 は,角速度ベクトルに角運動量ベクトルを次のように対応させます.
は,角速度ベクトルに角運動量ベクトルを次のように対応させます.
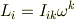
デカルト座標では反変と共変の区別はありませんが,一般化する場合を考慮して添字を上下に書き分けました.
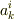 を変換行列とする座標変換
を変換行列とする座標変換 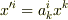 を行って
を行って
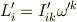
となったとすると, 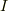 と
と 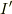 の間には
の間には
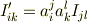
という関係があることが導かれます.従ってこのように変換される量としてテンソルを定義することもできるわけです.
なお,変換行列 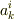 はテンソルではありません.
はテンソルではありません.
Re: テンソル
ファイル さんのレス (2008/11/13(Thu) 18:28)
せっかくご説明いただいたのに,返事が大変おそくなり,申し訳ありませんでした.
>数学では後者が主流で,私もこの定義の方が,抽象的だが,本質が見えるのですきです. ここでtoorisugari no Hiroさんがおっしゃる「後者」とは 「ベクトル(や双対ベクトル)を引き数とし,スカラー値を返す(多変数)線形関数」 のことですよね?
線形関数としての立場からテンソルを定義している本を見つけたので,読んでいたのですが,双対ベクトルという言葉もそこで初めて知りました. まだ,全部読んだわけではないのですが,普通のベクトルと逆の変換をされるものを双対ベクトルと呼ぶ,というので合ってますか? その本によると,反変とか,共変という言葉は古いもので今はあまり使われないと書いてありました.(相対論だと,普通に反変,共変で習ったのですけど・・・)
ベクトルに関しては(2)が定義で,それによって定義されるベクトルの座標変換の性質を調べると,(3)のようになる,と考えていたので,異なる定義があってもすんなり受け入れることが出来ました.同様に,テンソルを「ベクトルを引数としてスカラーを返す線形関数」と考えると,自然に,座標変換法則も導かれる.と考えました.
例えば,1つのベクトルをスカラー値にする線形関数,テンソルTを考え,基底を 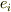 から
から 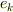 に座標変換すると
に座標変換すると
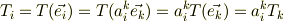
となって,線形関数としての定義から, テンソルTの成分が,基底ベクトルと同じ座標変換をする(つまり,テンソルTは共変ベクトル)ことが導かれる. と理解したのですが,この考え方であってますでしょうか?
yamaさんの論法も,そういうことですよね?
Re: テンソル
toorisugari no Hiro さんのレス (2008/11/14(Fri) 00:11)
> 「後者」とは ... > のことですよね?
そうです.
> 普通のベクトルと逆の変換をされるものを双対ベクトルと呼ぶ,というので合ってますか?
間違いではないですが,それは「反変とか,共変」に沿った概念ですね.
双対ベクトルとは,ベクトル空間 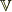 の元を引数とし実数値を返す線形関数全体の集合
の元を引数とし実数値を返す線形関数全体の集合 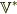 の元です.(もし,ベクトル空間
の元です.(もし,ベクトル空間 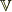 に内積(=計量)が定義されているなら,
に内積(=計量)が定義されているなら, 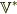 の元と
の元と 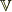 の元は一対一対応します.)
の元は一対一対応します.)
これではあまりにも,抽象的過ぎますが,図形的にいえば,「有向線分」と「有向平行平面群」(以下,「有向層」)がそれぞれ「ベクトル」と「双対ベクトル」に対応します.
#「ベクトル」,つまり「有向線分」,として変位ベクトル( 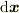 )を考えます.「有向層」は等間隔に平行に並んだ平面の集まりで,平面波に相当します(進行方向が与えられているとします).「波」の波数ベクトル
)を考えます.「有向層」は等間隔に平行に並んだ平面の集まりで,平面波に相当します(進行方向が与えられているとします).「波」の波数ベクトル 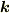 が「双対ベクトル」です.変位ベクトルに対して線形関数が返す実数値は波の「位相」(
が「双対ベクトル」です.変位ベクトルに対して線形関数が返す実数値は波の「位相」( 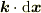 )に相当します.
)に相当します.
もし,「有向線分」と「有向層」が『平行』だとします.(線分が平面に『垂直』の場合です.)
線分方向に空間を2倍に引き延ばすと「有向線分」の大きさは2倍になりますが,「有向平行平面群」の大きさは1/2倍になります. #波数ベクトルは波長の逆数に比例することを思い出してください.
この様から,それぞれのベクトルを,「共変,反変」と呼ぶわけです.
Re: テンソル
ファイル さんのレス (2008/11/15(Sat) 01:53)
>内積(=計量)が定義されているなら 「一対一対応します」というのは,計量(内積)によって添え字の上げ下げ つまり,ベクトルから双対ベクトル,あるいは双対ベクトルからベクトルに変えることが出来る,という解釈でよろしいですか?
双対ベクトルの
上の定義と,その下の図形は理解できました.
双対ベクトル,ベクトルをそれぞれ 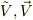 とすると
とすると
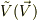 が実数ということですよね.
私のもっている本によると,逆に
が実数ということですよね.
私のもっている本によると,逆に 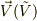 でも同じ値を返すようなのですが,それが「双対」という意味なのでしょうか.
でも同じ値を返すようなのですが,それが「双対」という意味なのでしょうか.
それと,下の図形は理解できましたが,こういうふうにイメージする意味?がよくわかりません.双対ベクトルは線形関数で,そこから自然に「反変,共変」の意味が導かれる,という感じでしょうか.
Re: テンソル
toorisugari no Hiro さんのレス (2008/11/17(Mon) 12:39)
> それと,下の図形は理解できましたが,こういうふうにイメージする意味?がよくわかりません.
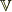 を3次元ベクトル空間とし,
を3次元ベクトル空間とし, 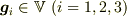 を互いに独立なベクトルとします.
を互いに独立なベクトルとします.
恒等的には0ではない線形関数 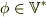 に対して,
に対して,
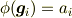
となるとします.
このとき, 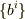 をパラメータとして
をパラメータとして
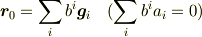
で表せる 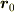 は
は 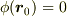 を満たします.点
を満たします.点 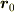 が作る幾何は原点を通る平面であり,これを
が作る幾何は原点を通る平面であり,これを 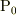 とよびます.また,
とよびます.また,
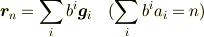
がつくる幾何は平面 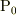 に平行な平面(
に平行な平面( 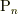 )であり,
)であり, 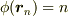 となります.
となります.
つまり, 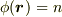 で表せる等値面は
で表せる等値面は 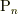 ということです.
ということです.
# 以上の話が理解しづらいなら,次のように考えることもできます.
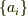 のすべてが0ではないですから,仮に
のすべてが0ではないですから,仮に 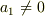 とします.すると
とします.すると
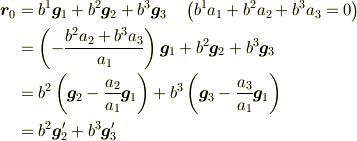
となり 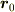 は原点を通る平面であることが分かります.また,
は原点を通る平面であることが分かります.また,
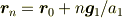
がつくる幾何は平面 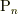 であり,
であり, 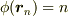 を満たすことも分かると思います.
を満たすことも分かると思います.
 を整数とすれば,
を整数とすれば, 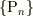 は平面群(有向層)を表します.(必要なら,0.1刻み,0.01刻み..で作っても良いです).
は平面群(有向層)を表します.(必要なら,0.1刻み,0.01刻み..で作っても良いです).
この有向層が関数  と対応します.
と対応します.
変位ベクトル 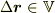 に対して
に対して 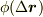 の値は,層
の値は,層 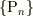 のなかに
のなかに 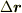 を置いたときの,平面との交点の数(補助平面も使えば実数値)と対応します.
# これは
を置いたときの,平面との交点の数(補助平面も使えば実数値)と対応します.
# これは 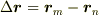 で考えれば明らかですね.
# さらに正確に言えば「平面との交点の数」ではなく,「平面間の空隙を跨いだ数」です.
で考えれば明らかですね.
# さらに正確に言えば「平面との交点の数」ではなく,「平面間の空隙を跨いだ数」です.
ベクトル  → 矢印ベクトル
線形関数
→ 矢印ベクトル
線形関数  → 有向層
実数値
→ 有向層
実数値 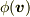 → 交点の数
# 有向層を平面波と考えれば,交点の数は「山の個数」すなわち位相
→ 交点の数
# 有向層を平面波と考えれば,交点の数は「山の個数」すなわち位相 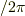 ですね.
ですね.
これが 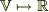 となる線形関数,すなわち,双対ベクトルの3次元の場合の図示化になります.
となる線形関数,すなわち,双対ベクトルの3次元の場合の図示化になります.
# なお,この段階では,ベクトルの大きさや成分,あるいは,直交,といった「内積」を定義しないと出てこない概念は使ってません.
Re: テンソル
ファイル さんのレス (2008/11/23(Sun) 21:14)
ありがとうございます. おかげさまで,ベクトルと双対ベクトル,テンソルに関して系統的な理解が(ある程度ですが・・・)出来ました.
このような数学は,どのような物理で使われるのでしょうか? 今,相対性理論を勉強しているのですが,テンソルに関してクローズアップされるのは座標に対しての変換性だけですね・・・. 計量が内積というのはたまに出てきます.
Re: テンソル
toorisugari no Hiro さんのレス (2008/11/25(Tue) 10:37)
> このような数学は,どのような物理で使われるのでしょうか?
一般相対論はもろに使いますね.ただ,教科書によっては,テンソルの添え字の上げ下げ操作ですませていて,双対ベクトルという概念が表には出ないものも多いです.
しかし,双対,さらにp-vectorとp-formの変換をするホッジの*双対(体積要素をかけたり割ったり)という概念を知っていると,密度テンソルがよりよく分かります.
これらの概念によって例えば電磁気学では方程式の構造が非常に簡単になり理解し易くなります.また,素粒子の世界にいくともっと高度なトポロジーの概念も使います.
詳しくは
- http://www.amazon.co.jp/%E7%89%A9%E7%90%86%E5%AD%A6%E3%81%AB%E3%81%8A%E3%81%91%E3%82%8B%E5%B9%BE%E4%BD%95%E5%AD%A6%E7%9A%84%E6%96%B9%E6%B3%95-%E7%89%A9%E7%90%86%E5%AD%A6%E5%8F%A2%E6%9B%B8-B-F-%E3%82%B7%E3%83%A5%E3%83%83%E3%83%84/dp/4842702168/
- http://www.amazon.co.jp/%E7%90%86%E8%AB%96%E7%89%A9%E7%90%86%E5%AD%A6%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AE%E5%B9%BE%E4%BD%95%E5%AD%A6%E3%81%A8%E3%83%88%E3%83%9D%E3%83%AD%E3%82%B8%E3%83%BC%E3%80%881%E3%80%89-%E4%B8%AD%E5%8E%9F-%E5%B9%B9%E5%A4%AB/dp/4894711656/
- http://www.amazon.co.jp/%E7%90%86%E8%AB%96%E7%89%A9%E7%90%86%E5%AD%A6%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AE%E5%B9%BE%E4%BD%95%E5%AD%A6%E3%81%A8%E3%83%88%E3%83%9D%E3%83%AD%E3%82%B8%E3%83%BC%E3%80%882%E3%80%89-%E4%B8%AD%E5%8E%9F-%E5%B9%B9%E5%A4%AB/dp/4894714264/
を読んでください.
このような数学の概念を知らなくても物理を理解することは可能ですが,知っているとより系統的に理解できるので,若いうちに勉強することをお勧めします.
Re: テンソル
ファイル さんのレス (2008/11/25(Tue) 22:27)
ありがとうございます. 三冊とも,「幾何学」とありますが,微分幾何学という分野のことですよね? 実は,相対論はシュッツで勉強していました.ご紹介いただいた一冊目も同じ著者なので,読んでみたいと思います.
Re: テンソル
toorisugari no Hiro さんのレス (2008/11/25(Tue) 23:03)
> 微分幾何学という分野のことですよね?
そうです.多様体とか微分形式といった概念が出てくる分野です.