Kerr解の座標変換
Kerr解の座標変換
トビラ.. さんの書込 (2008/11/04(Tue) 23:51)
ボイヤーリンキスト座標を導出する過程の話なのですが,いろいろな方法があると思いますが,これが何という方法なのかよくわからないので,説明不足かもしれませんがわかる方どうか説明をお願いします.まず,Kerrの解を導出したとします.それが
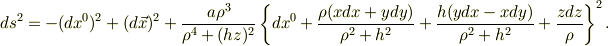
ここで  と
と  の関係は
の関係は 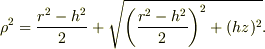 です.
このそれぞれの記号の意味例えば
です.
このそれぞれの記号の意味例えば 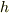 などを僕は説明しずらいので,本によって使っている記号は違うと思いますが式の類似性から読み取ってください(すみません)
このKerr解をほかの座標系に変換するときによく
などを僕は説明しずらいので,本によって使っている記号は違うと思いますが式の類似性から読み取ってください(すみません)
このKerr解をほかの座標系に変換するときによく
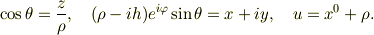
という座標変換をすると思うのですが,なぜこのような奇妙な座標変換になるのか,よくわからないのでどうか教えてください.たとえば,座標変換の第2式の
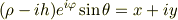
のような変換の意味がよくわかりません.(変換そのものの計算はできるのですが) 説明不足で本当に申し訳ないです.
Re: Kerr解の座標変換
スパイク さんのレス (2008/11/07(Fri) 22:29)
こんばんは.
おそらく,物理数学(語)と表現すべきでしょうか, トビラ..さんにとって,翻訳しづらいのではないかと推測されます.
私には,軸対称で,それと(角運動量を考慮した)直交した平面に対称性を持つ,時間依存性のある座標への変換ですよ. と受け取れるのですけど...
#この分野では,個性的な方(もしくは特有の表現)は,多いと思われますが.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/07(Fri) 22:56)
こんばんわw 相変わらず素敵なブロクですね.
うぅぅぅぅん,物理数学(語)ってどこに行けば教えてくれるんですか?(ノバ?) 数式を見ただけで意味を読み取れるなんてうらやましいです.
できれば,第2式の奇妙な形の数式の意味だけでもいいので僕にも理解できるように教えてください. (ブログに書いてくれてもいいですよ)
Re: Kerr解の座標変換
スパイク さんのレス (2008/11/07(Fri) 23:41)
文字と数式では,結構辛い部分もありますが;) 私なりに,第2式に限定しますと,概要としては(?)
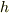 が角運動量に対応しており,
虚数単位(
が角運動量に対応しており,
虚数単位( 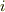 )が,時間に対応しています.
このことから,
)が,時間に対応しています.
このことから, 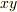 平面で,回転している
描像が,浮かんできます.これは,座標が角度依存性
(
平面で,回転している
描像が,浮かんできます.これは,座標が角度依存性
(  ,
,  )を持つことから分かります.
角度依存性につきましては,(
)を持つことから分かります.
角度依存性につきましては,(  ,
,  )の
二変数によることから,円筒状ではなく,軸(
)の
二変数によることから,円筒状ではなく,軸(  )に対して,
上下に対称性を持つ,(この場合は末広がりでしょうか?)形状を描くことが分かります.
)に対して,
上下に対称性を持つ,(この場合は末広がりでしょうか?)形状を描くことが分かります.
#ルービックキューブに詳しいと,何となく判ったような気になるかも? #まずは,ご参考になれば幸いです.
)計量中の分母の余弦は,二乗になるかと思います.一応,念のため. **)確認したところ,ボイヤーリンキスト座標での計量の計算結果は合っています. **)後は,余裕があれば,各項の物理的解釈といったところでしょうか(特に第5項).
Re: Kerr解の座標変換
toorisugari no Hiro さんのレス (2008/11/08(Sat) 00:07)
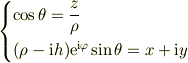
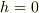 なら,直角座標系
なら,直角座標系 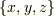 から極座標系
から極座標系 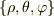 への変換式そのものですね.
への変換式そのものですね. 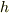 は
は  一定の面を球面から
一定の面を球面から 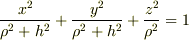 へと扁平化する効果をもちますが,
へと扁平化する効果をもちますが, 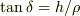 で示される角度
で示される角度  の意味は分かりかねます.
の意味は分かりかねます.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/08(Sat) 06:02)
スパイクさんありがとうございます.直観的な数式の見方は大切ですね.とても為になりました.(僕もいつかそんな力つけたい.)
toorisugari no hiroさんまたも,お世話になりました.自分の中のもやもや感が消えてとてもすがすがしいです.
以下のようなことですよね?
座標変換 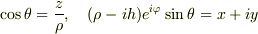 という変換は
まず第2式から
という変換は
まず第2式から 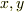 を求めると,
を求めると,
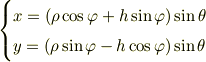
でしたがって 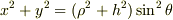 となる.ゆえに
となる.ゆえに
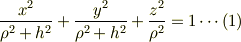
という関係式が導出される.
この式(1)の意味は,第1項と第2項を合わせて  平面の
平面の 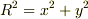 を定義すると式(1)は
を定義すると式(1)は
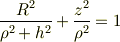
となり,これはまさに楕円の形をしている.また,(1)式の第1項と第2項だけを考えると円形の形をしている.
まとめて言い換えると,  -軸に垂直な方向から眺めた場合
-軸に垂直な方向から眺めた場合 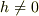 で楕円の形をしていて,
で楕円の形をしていて,  -軸に対して対象である.また,
-軸に対して対象である.また,  -軸に並行な方向から眺めた場合,円対称(?)なので原点(
-軸に並行な方向から眺めた場合,円対称(?)なので原点(  -軸)に対して対象である.
したがって,この座標変換は
-軸)に対して対象である.
したがって,この座標変換は  -軸に対称な座標
-軸に対称な座標 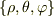 への変換である.
ということですよね?
本当にありがとうございます.とてつもなく助かりました.
への変換である.
ということですよね?
本当にありがとうございます.とてつもなく助かりました.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/08(Sat) 06:17)
恐縮ながら,もう一つ質問すると新たな時間変数を 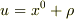 とする必要性はなんですか?この式はどのようなことをを意味するんでしょうか?
時間変数には球対称性を持たせようという考えなのでしょうか?
とする必要性はなんですか?この式はどのようなことをを意味するんでしょうか?
時間変数には球対称性を持たせようという考えなのでしょうか?
Re: Kerr解の座標変換
スパイク さんのレス (2008/11/08(Sat) 10:40)
おはよう御座います.
理解が進んだようで,良かったですね.
>時間変数には球対称性を持たせようという考えなのでしょうか?
今手元に資料がないのですが,恐らくそうだと思われます.
Re: Kerr解の座標変換
toorisugari no Hiro さんのレス (2008/11/08(Sat) 14:30)
> まず第2式から 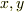 を求めると,
>
を求めると,
>
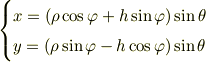
ここは
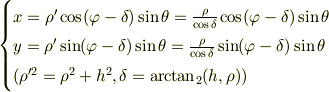
とすれば,見通しは利きますね.
> この座標変換は |fbade9e36a3f36d3d676c1b808451dd7| -軸に対称な座標 |11e08372e0d9e14c12e1c48535ed828e| への変換である.
ということですよね?
というか 軸対称引き延ばし変換と極座標変換の合成でしょう.
> 時間変数には球対称性を持たせようという考えなのでしょうか?
球対称性が3次元の意味か,4次元の意味か分かりかねますが,後者なら,
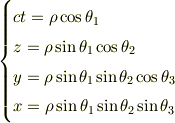
とでもするでしょうが,これは相対論的に無意味な変換ですよね.
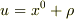 は中心から離れるにつれて時間の進み方が変化する効果を考慮して「同時刻」を修正したものなのでしょうが,きちんとしたことは何もわかりません.
は中心から離れるにつれて時間の進み方が変化する効果を考慮して「同時刻」を修正したものなのでしょうが,きちんとしたことは何もわかりません.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/08(Sat) 18:36)
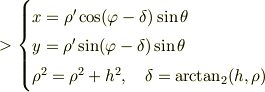
とすればみとうしがよくなる
とあるんですけど,このように複雑な計算をしなくてもしなくても 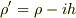 と定義すると
と定義すると
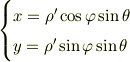
と見通しは良くなると思います.( 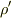 に虚数が含まれますけど)
に虚数が含まれますけど)
この座標変換を始めて考えた人はどのようにこの座標変換自体を導出したのでしょうか?やはり,もととなったkerrの解をみて(1)式との類似性によりこのような座標変換を導出したのでしょうか?
>球対称が3次元の意味か4次元の意味かわかりかねますが
一般相対性理論は4次元空間ではなく4次元時空の物理学ですから,3次元の方をさしているつもりでした.
シュバルツシルド座標の場合,事象の地平線で時間の計量が無限に発散するので時間変数 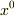 に有限値
に有限値  を足しても同時の修正にそれほど効果があるようには思えないんですけどどうなんでしょうか?それとも,一回
を足しても同時の修正にそれほど効果があるようには思えないんですけどどうなんでしょうか?それとも,一回
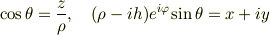
と座標変換した後で, 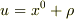 とおいた方が座標系が見やすくなるということに気づき,後から付け加えた変換なのかもしれませんね.
この座標変換の意味を聞いておきながら,この座標変換の導出の話にすりかえてすみません.
とおいた方が座標系が見やすくなるということに気づき,後から付け加えた変換なのかもしれませんね.
この座標変換の意味を聞いておきながら,この座標変換の導出の話にすりかえてすみません.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/08(Sat) 19:04)
すみません.見通しが利きます.ってかいていたんですね(汗)
見通しが良くなるって書いているのかと思ってました.すみません.
でもなんで,初めてこの座標変換を導出した人は 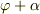 の変換の
の変換の  に
に 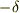 を採用したのでしょうか?
を採用したのでしょうか?
Re: Kerr解の座標変換
toorisugari no Hiro さんのレス (2008/11/08(Sat) 20:14)
> でもなんで,初めてこの座標変換を導出した人は 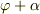 の変換の
の変換の  に
に 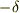 を採用したのでしょうか?
を採用したのでしょうか?
単に「計算が楽なるから複素数表示にした.その代わり  が導入されたが,問題ないので無視.」ぐらいじゃないでしょうかね.
が導入されたが,問題ないので無視.」ぐらいじゃないでしょうかね.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/08(Sat) 22:14)
スパイクさん,toorisugari no hiroさんどうもありがとうございました. 大変助かりました.
Re: Kerr解の座標変換
mNeji さんのレス (2008/11/09(Sun) 09:07)
横から失礼します.
素人ながら,興味深く論議を拝見していました.
特に,次の関係;
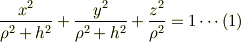
には感動しました.
球対称の質量分布が在った時に,それがz軸について回転しているとすれば,遠心力効果で,等重力ポテンシャル面が変形されるのではなかろうかと推量していたからです.
私は,数学が苦手な為に,一般相対性理論には興味が在るものの,近寄り難いものと考えていました.でも,今回のトビラ..さんの論議を拝見していて,やはり面白い分野だなと感じました.
これから勉強を続けて,逆に,素人にも優しい解説を書かれる事を希望します.ヤッホー!
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/09(Sun) 23:12)
mNejiさん久しぶりです. って覚えてないか・・・実はこの前までチャパって名前でした.分け合って名前を変えたんですけども,以前mNejiさんは内山龍雄さんの弟子の砂川さんの理論電磁気の一辺倒だったって聞いて感動しました.(内山龍雄さんのことすごく尊敬しているので,ある意味つながりがもてた気がしてうれしかったんです.)
で,本題に入りますけども,
>球対称の質量分布が在った時に,それがz軸について回転しているとすれば,遠心力効果で,等重力ポテンシャル面が変形されるのではなかろうかと推量していたからです.
なるほど,そう考えるとkerr解に対してこのような座標変換するのは自然ですね. 物理的な意味に気付かなかったです.もわもわ感が完全に晴れた気がします. toorisugari no hiroさんもそのような意味で言っていたのでしょうね.気付かずすみませんでした. どうもありがとうございました.
Re: Kerr解の座標変換
mNeji さんのレス (2008/11/09(Sun) 23:37)
トビラ..さん,チャパさんの事なら覚えていますよ.HNが替わっただけでなく,進化が凄いので驚きました.
>って覚えてないか・・・実はこの前までチャパって名前でした.分け合って名前を変えたんですけども,以前 mNejiさんは内山龍雄さんの弟子の砂川さんの理論電磁気の一辺倒だったって聞いて感動しました.(内山龍雄さんのことすごく尊敬しているので,ある意味つながりがもてた気がしてうれしかったんです.)
う〜む,砂川さんには一度もお会い出来ませんでしたが,いまでも思考の透明性には深く打たれるところが在ります.
昨年,優秀な後輩の方と話していた時に,内山さんと砂川さんのお話を教えて下さり,内山さんの相対性理論の本を読むように,本まで渡されてしまったのですが,怪我をして入院してしまい,万が一を考えて返却してしまいました,残念(笑).
年齢もえらく違っているのですが,思考上の兄弟弟子のトビラ..さんの質問を,今後も楽しみにしています.
>なるほど,そう考えるとkerr解に対してこのような座標変換するのは自然ですね.物理的な意味に気付かなかったです.もわもわ感が完全に晴れた気がします.
あくまで素人のゲスなので考える時のヒント程度にしておいて下さい.「完全な理解」に達したら,ぜひとも解釈を教えてくださいね.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/10(Mon) 00:14)
>年齢もえらく違っているのですが,思考上の兄弟弟子のトビラ..さんの質問を,今後も楽しみにしています.
え?本当に?弟子にしてくれるの?やったぁぁぁぁ!!!デヘヘ 師匠・・・ってかマスターmNejiって呼んでいい?(スターウォーズみたいに) いや,やっぱ師匠で・・・ また何か疑問があればここで質問します.(質問できる人,周りにいないから助かります.) フォースとともにあれ・・・
Re: Kerr解の座標変換
toorisugari no Hiro さんのレス (2008/11/10(Mon) 11:59)
参考のため座標変換された計量を書いてもらえますか?
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/10(Mon) 23:18)
上の失敗したんですけど,なぜか削除できないので,上のは無しで. 改めて書きます.
ああはい,ちなみにその前に  の符号をかえて
の符号をかえて 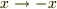 とします.そうしたうえで
とします.そうしたうえで
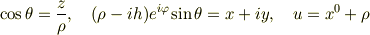
の座標変換をすると
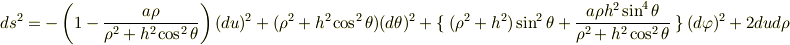
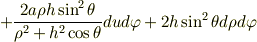
となるんです.計算大変です.(汗)
Re: Kerr解の座標変換
toorisugari no Hiro さんのレス (2008/11/11(Tue) 11:38)
ありがとうございます.思ったほどきれいにはなりませんね. # 途中を計算してないので,結果がどれほど単純か分からないだけですけど.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/11(Tue) 12:24)
そうですね.あまり綺麗ではないですね. ただ,この式はボイヤーリンキスト座標を導出する過程の式なので,まだ結果ではないんです.これからこの式をいじってもっとシンプルになっていくんですけどね.
Re: Kerr解の座標変換
トビラ.. さんのレス (2008/11/11(Tue) 23:21)
うひゃー書けってことか(笑) ちょっと省略・・・ってか結構省略して結果だけを述べるとボイヤーリンキスト座標は
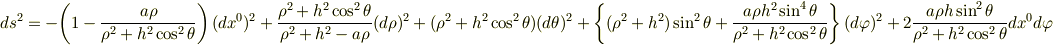
となります. 詳しい計算はこのホームページで書いています.(このホームページの人かなりすごいです.)
Re: Kerr解の座標変換
toorisugari no Hiro さんのレス (2008/11/12(Wed) 12:19)
完成したら,でよかんたですけどね.:-) クロスタームは一個に減り,だいぶすっきりとしましたが,やっぱり複雑ですね.
