ローレンツ変換
ローレンツ変換
えり さんの書込 (2008/11/02(Sun) 16:51)
お久しぶりです. 特殊相対性理論の授業で,マックスウェルの方程式がローレンツ変換のもとで不変であるとうことを確かめてみてと先生に言われて解いてみたのですが,形が変わってしまいます..
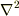 のところで既に形が変わってしまいます.
解き方としては
のところで既に形が変わってしまいます.
解き方としては
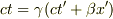
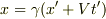
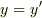
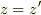 を使って波動方程式に代入すればいいのですよね?
を使って波動方程式に代入すればいいのですよね?
Re: ローレンツ変換
yama さんのレス (2008/11/02(Sun) 23:42)
それだけでは空間座標と時間についてのローレンツ変換しか考えていないことになります. 電磁場(の成分)もローレンツ変換されることに注意しましょう.
Re: ローレンツ変換
えり さんのレス (2008/11/03(Mon) 00:15)
電磁場の成分とは,波動方程式に含まれるBとEの成分のことですよね?
Re: ローレンツ変換
サボテン さんのレス (2008/11/03(Mon) 14:37)
横から失礼します. そうです. 電磁場(ベクトルポテンシャル)や座標はSO(3,1)によって,ベクトルとしての変換を受けるので, 同じように扱ってやる必要があります.
Re: ローレンツ変換
yama さんのレス (2008/11/03(Mon) 17:39)
補足しておきます.
4元ポテンシャル 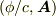 は4元ベクトルとして変換されます.
一方,4元ポテンシャルから導かれる
は4元ベクトルとして変換されます.
一方,4元ポテンシャルから導かれる 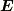 や
や 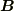 の成分は2階反対称テンソルの成分として変換されます.
また,電荷電流密度
の成分は2階反対称テンソルの成分として変換されます.
また,電荷電流密度 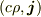 は4元ベクトルとして変換されます.
は4元ベクトルとして変換されます.