球対称な４次元不変距離

home > 掲示板 >

このページのPDF版

サイトマップ

球対称な４次元不変距離

トビラ．．さんの書込 (2008/11/02(Sun) 13:47)

おはようございます．（と言ってももう昼ですけども）少し前Einstein方程式の厳密解を勉強して疑問に思ったことがあるので質問したいのですけども，静的，球対称な４次元不変距離 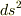ds^2 の最も一般的な形についてなのですが

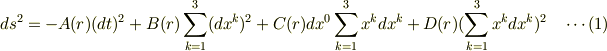
$ds^2=-A(r)(dt)^2+B(r)\sum^3_{k=1}(dx^k)^2+C(r)dx^0\sum^3_{k=1}x^kdx^k+D(r)(\sum^3_{k=1}x^kdx^k)^2\quad \cdots(1)$

が最も一般的な静的，球対称というかたちですよね？これに時間反転に対して不変という条件をつけると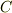は０となり，また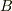，は必ず１とおくことができる．ということは理解できるのですが，なぜこの式（時間反転に対して不変という条件を付ける前の(1)式）に 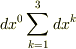$dx^0\sum^3_{k=1}dx^k$ という項がないのですか？また 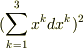$(\sum^3_{k=1}x^kdx^k)^2$ という項がなぜ球対称いう４次元不変距離 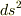ds^2 の中に含まれているのかが理解できない，というか，この項の意味はどのような意味なのかがわからないので，どうか説明お願いします．

Re: 球対称な４次元不変距離

トビラ．．さんのレス (2008/11/02(Sun) 14:01)

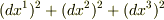あ！すみませんわかった気がします（汗）球座標に変換すると確かにだけで第３，４項は表現されています．そして第２項は (dx^1)^2+(dx^2)^2+(dx^3)^2 なのでこれも球対称という条件を満たしているこうということも理解できます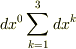． $dx^0\sum^3_{k=1}dx^k$ という項がないのも球座標に変換すると理解できます．すみません，もっとよく考えて質問することにします．一応この考えであっているのでしょうか？

Re: 球対称な４次元不変距離

サボテンさんのレス (2008/11/03(Mon) 14:33)

球対称ということは3次元空間上でkの添え字を縮約する必要があります (相対論で言うところのスカラーを作る操作と同じです)

例えば?dx^kと言う項は添え字kが残っているため，SO(3)不変ではありません．第2項はdx_kdx^kと書けるため，kが縮約され，SO(3)不変量です．

Re: 球対称な４次元不変距離

トビラ．．さんのレス (2008/11/04(Tue) 22:20)

サボテンさんわかりやすい回答ありがとうございます．つまり，縮約しないとベクトル量なので方向によって変わってしまうけども，縮約してスカラー量にすると方向にはよらず原点からの距離だけによる量になるため球対称となる．ということですか？もやもや感がなくなりました，回答ありがとうございます．

[home] [掲示板] [ページの先頭]