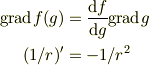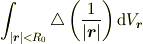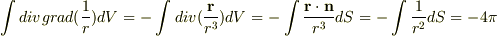また,デルタ関数です.すみません.
また,デルタ関数です.すみません.
snow さんの書込 (2008/10/31(Fri) 19:09)
次の式が成り立つそんなんですが,どうしてかよくわかりません.
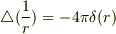 一様自分でも調べてみたけど,超関数?とかよくわかりませんでした.
お願いします!!
一様自分でも調べてみたけど,超関数?とかよくわかりませんでした.
お願いします!!
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/10/31(Fri) 19:25)
(1)ガウスの発散定理,ご存じですか?
(2)(スカラー)ラプラシアンを 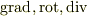 で表すと?
(3)
で表すと?
(3) 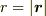 として
として 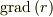 の値は?
の値は? 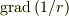 の値は?
(4)球面における面積積分
の値は?
(4)球面における面積積分
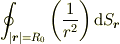
の値は? (5)球における体積積分
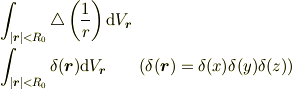
の値は?
(4)くらいまでは自力でやってきてくださいね.
# 記法に間違いがあったので修正しました.
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/10/31(Fri) 19:54)
あぁ,ガウスの発散定理かぁ.えーと,
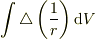 は立体角になりますね.
だから,
は立体角になりますね.
だから, 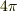 で,
で,
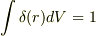 よって,
よって, 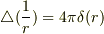 でいいのかな?
あれ?マイナスの符号が・・・.
でいいのかな?
あれ?マイナスの符号が・・・.
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/10/31(Fri) 20:00)
>あぁ,ガウスの発散定理かぁ.えーと,
> 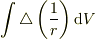 は立体角になりますね.
は立体角になりますね.
これは発散定理ではありません.
> あれ?マイナスの符号が・・・.
きちんと最初から計算しませんか?
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/10/31(Fri) 20:15)
えーと,
 積分範囲が
積分範囲が 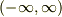 なので,
なので,
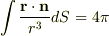 だと思ったのですけど・・・.
だと思ったのですけど・・・.
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/11/01(Sat) 14:24)
が何故負になるのでしょう.
予定調和(=結論誘導)な考え方はやめた方がいいです.
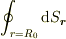 の値は求められますか?
の値は求められますか?
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/11/01(Sat) 14:57)
そうですね.どうも,予定調和な考え方をすぐしてしまいます.
悪い癖ですね.以後,気をつけます.
えーと,
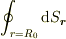 の値ですか・・・.
よくわかりません.
の値ですか・・・.
よくわかりません.
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/11/01(Sat) 15:30)
え?絵ですか? ・・・・. 球の表面積ってことですか?
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/11/01(Sat) 15:36)
> 球の表面積ってことですか?
そういうことです. 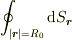 という式を日本語に変換できないと,球の表面積になることを実感できないとは思いますが...
という式を日本語に変換できないと,球の表面積になることを実感できないとは思いますが...
で 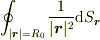 の値は?
式をよくみれば,変形できますね.
の値は?
式をよくみれば,変形できますね.
# 記法を変えました.
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/11/01(Sat) 18:07)
変形ですか? ん〜.ヒントください.
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/11/05(Wed) 21:22)
すみません.マジでわかりません.
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/11/05(Wed) 21:49)
> すみません.マジでわかりません.
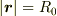 という式の意味がわかりますか?
どういう図形を指しているのか分かりますか?
という式の意味がわかりますか?
どういう図形を指しているのか分かりますか?
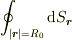 の値は分かりますか?
の値は分かりますか?
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/11/06(Thu) 00:25)
> 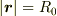 は
は 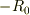 から
から 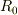 の範囲で積分するって意味では?
の範囲で積分するって意味では?
 は位置ベクトルです.
は位置ベクトルです. 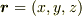 と置いたとき,
と置いたとき,
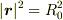 を
を 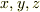 で書き換えてください.
これはどういう図形を指しているのか分かりますか?
で書き換えてください.
これはどういう図形を指しているのか分かりますか?
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/11/06(Thu) 00:40)
あー,半径 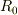 の球ってことですか?
の球ってことですか?
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/11/06(Thu) 01:04)
> あー,半径 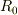 の球ってことですか?
の球ってことですか?
...球でなく,球面です...(球は 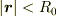 )
)
ですから,
「 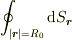 は,
(閉曲面
は,
(閉曲面 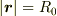 を複数の微小な領域に分割し,一つの領域の代表点を
を複数の微小な領域に分割し,一つの領域の代表点を 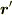 とし(
とし( 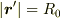 ),その領域の微小面積を
),その領域の微小面積を 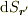 であらわすとして,)
閉曲面
であらわすとして,)
閉曲面 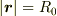 上のすべての微小面積を足し合わせたものである.」
上のすべての微小面積を足し合わせたものである.」
と読みますが,これは半径 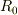 の球面の面積そのものです.
の球面の面積そのものです.
これは「表現」のための積分式であって,このままでは値を「計算」できません.値を求めたいときには適当な座標系を決めます.これは分割の仕方を指定することに等価です.直角座標系でも計算はできますが,極座標系で計算するのが普通です.
すると,半径 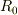 の球面上の緯度
の球面上の緯度  ,経度
,経度  にある代表点を含む微小面積は,
にある代表点を含む微小面積は, 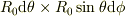 と表せるので,
と表せるので,
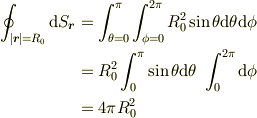
となります.
さて, 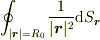 の値はもう分かりましたか?
の値はもう分かりましたか?
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/11/07(Fri) 00:11)
# もう飽きちゃったと思っていました.
> えーと, >
> ですよね.
一番目は正解ですが,2番目は間違い.
Re: また,デルタ関数です.すみません.
snow さんのレス (2008/11/07(Fri) 00:47)
あ,マイナスを付け忘れてました.すみません.
Re: また,デルタ関数です.すみません.
toorisugari no Hiro さんのレス (2008/11/07(Fri) 01:31)
あってます. これと,
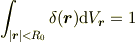
を組み合わせると,目標の
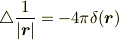
がえられますね.(厳密には,原点が球の外にある場合も考えなければいけないのですが,略.)
ご苦労様です.
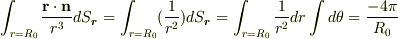 ここまであってますか?
ここまであってますか?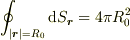 ではないでしょうか.
ではないでしょうか.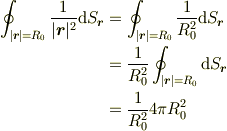
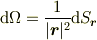
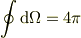
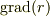 ,
, 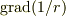 を計算する番ですね.
を計算する番ですね.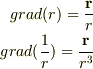 ですよね.
ですよね.