調和条件

調和条件

トビラ．． さんの書込 (2008/10/31(Fri) 00:38)

こんばんわ．トビラ．．と言います．重力波を勉強していてつまづきました．トホホ

De Donderの条件（調和条件）についてなのですが，一般には次の数式は成り立たつのですか？

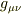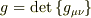g_{\mu\nu} は計量テンソル， g=\det \left\{g_{\mu\nu}\right\} として，また，計量テンソルの空間成分の符号はプラス，時間成分の符号はマイナスとします． そうすると

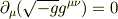
\partial_\mu(\sqrt{-g}g^{\mu\nu})=0

という関係は一般には成り立つのでしょうか？ミンコフスキー型の時空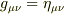（ g_{\mu\nu}=\eta_{\mu\nu} ）ならこの関係は成り立つとおもうのですが，一般には成り立たない気がします．それとも，測地系をとればテンソル密度の共変微分より右辺は０になる気はするのですがどうなのでしょうか，どうか助言をお願いします．

Re: 調和条件

スパイク さんのレス (2008/10/31(Fri) 06:44)

おはよう御座います．

一般には，成り立たないため，上式を満たすような適当な測地系を取ることにより，扱いやすくしていたかと思います．

＃基本的には，曲率のお話かと思われます．

Re: 調和条件

トビラ．． さんのレス (2008/10/31(Fri) 11:43)

おはようごさいますスパイクさん． 立派なブログですね．．

基本的には曲率の話ということですが曲率はどのように関係してくるのでしょか？ 僕は，次のように考えたんですけどあっていますか？ 共変微分の演算を 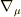\nabla_\mu として

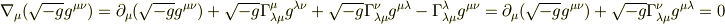
\nabla_\mu (\sqrt{-g}g^{\mu\nu})=\partial_\mu (\sqrt{-g}g^{\mu\nu})+\sqrt{-g}\Gamma^\mu_{\lambda\mu}g^{\lambda\nu}+\sqrt{-g}\Gamma^\nu_{\lambda\mu}g^{\mu\lambda}-\Gamma^\lambda_{\lambda\mu}g^{\mu\nu}=\partial_\mu (\sqrt{-g}g^{\mu\nu})+\sqrt{-g}\Gamma^\nu_{\lambda\mu}g^{\mu\lambda}=0

より

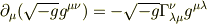
\partial_\mu (\sqrt{-g}g^{\mu\nu})=-\sqrt{-g}\Gamma^\nu_{\lambda \mu}g^{\mu\lambda}

なのでこの右辺のアフィン係数が０になるような測地系をとれば左辺は必ず０にすることが許される．という考えでよいのでしょうか？

Re: 調和条件

スパイク さんのレス (2008/10/31(Fri) 13:01)

今日は，トビラ．．さん．

そのような捉え方で，宜しいかと思います． ＃計算結果も合っているようです．

曲率というのは，曲線に対する接線の概念を 一般的に拡張したという意味です．

＃わざわざ，ブログまでお越しくださり，有難う御座いますm(_ _)m

2008.11.01のつぶやき *)方向性に間違いはないと思われます． **）曲率は，私も引きずっていたみたいです；）

2008.11.06のつぶやき *)一般的に広域には出来ないので，補正をかけると言うことなんですが．．．

Re: 調和条件

toorisugari no Hiro さんのレス (2008/10/31(Fri) 14:34)

私はわからないのでだまっていたのですが，

スパイクさん，知識がないのに教えるのはやめてください．

これは一階微分ですからおそらく接続か，擬重力系の話でしょう．それに「曲率というのは，曲線に対する接線の概念を一般的に拡張した」ものではありません．

Re: 調和条件

toorisugari no Hiro さんのレス (2008/10/31(Fri) 15:11)

私もよくわかっていなかったですね．本でざっとみたところ，ソース項がついてますね．

この条件は電磁気学のローレンツゲージみたいなもののようですね．

> 関係は一般には成り立つのでしょうか

ということですが，これはもちろん弱い重力場の範囲でのという意味ですよね． 電磁気の場合はゲージ変換により，成り立つように選ぶことができますが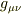， g_{\mu\nu} には(電磁気学の意味の)ゲージ変換はなさそうなので，きついですね．

内山の意味のゲージ変換でいけるのかもしれません．

少し時間をください．

Re: 調和条件

toorisugari no Hiro さんのレス (2008/10/31(Fri) 16:58)

> 共変微分の演算を 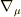\nabla_\mu として の計算はまだfollowしていませんが，

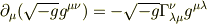
\partial_\mu (\sqrt{-g}g^{\mu\nu})=-\sqrt{-g}\Gamma^\nu_{\lambda \mu}g^{\mu\lambda}

が正しいとすれば，

> この右辺のアフィン係数が０になるような測地系をとれば左辺は必ず０にすることが許される．という考えでよいのでしょうか？

は正しいと思います．一般座標変換で 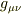g_{\mu\nu} を変換する事が，内山の意味のゲージ変換(だったと思います)から，筋はとおっています．

あ，localかglobalかは考えていなかった．全域で成り立たないとダメじゃないかな? そういう意味では「ソース項があっても(あるオーダーで)擬重力系であること」が条件と同値になりますね．

# だから「調和」条件か．．．．

globalな測地系はソース項があったら無理ですが，globalな(あるオーダーでの)「測地」系がとれるかなんて．．．．．

申し分けない．識者の出番を待ちましょう．

Re: 調和条件

yama さんのレス (2008/11/01(Sat) 10:38)

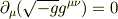
\partial_\mu(\sqrt{-g}g^{\mu\nu})=0

が一般に成り立つかと言えば，一般には成り立たないと言うべきでしょう． 左辺はテンソルの共変微分ではなく，普通の微分なので座標系によって変化するからです．

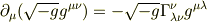
\partial_\mu(\sqrt{-g}g^{\mu\nu})=-\sqrt{-g}\Gamma^{\nu}_{\lambda\nu}g^{\mu\lambda}

は正しいと思います．この式からも一般には0にならないことが分かりますが，アフィン係数が0になるような測地系では当然0になりますね． しかし測地系は一般には局所的なものなので，全域で0にすることは一般にはできないでしょう． 全域で0にできるのは toorisugari no Hiroさんが言われるように，擬重力系に限られるように思います．

Re: 調和条件

トビラ．． さんのレス (2008/11/01(Sat) 13:38)

スパイクさん，toorisugari no hiroさん，yamaさんありがとうございます．

つまり，大局的な測地系がとれる擬重力系であればこの条件が満たされて，弱い重力場を近似的にかんがえるとこの擬重力系になる，ということですか？

すみません．勉強不足で「ソース項」の意味がわかりませんでした（汗）

Re: 調和条件

toorisugari no Hiro さんのレス (2008/11/01(Sat) 13:49)

> 勉強不足で「ソース項」の意味がわかりませんでした（汗）

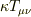ごめんなさい．電磁場の電荷密度，電流密度のように使ってました．エネルギー・運動量密度テンソルにEinsteinの定数 \kappa をかけた \kappa T_{\mu\nu} です． # だって長いんだもの．．

これが0なら全域で重力を消せるような系を採ることができますが，この問題では「ソース項」は小さいが0ではないというがやっかいな所です．(もしかして，私はここら辺で誤解をしているかもしれません．)

> 弱い重力場を近似的にかんがえるとこの擬重力系になる，ということですか？

そう願いたいところですが，実際に 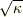\sqrt{\kappa} のオーダーで評価してみないと，この近似式が任意に成り立つか分かりません．

Re: 調和条件

トビラ．． さんのレス (2008/11/02(Sun) 02:36)

フムフム，なるほど，それをソース項っていうんですか． ＃長い説明ありがとうございます．

つまり，真空中を対象とするならばソース項は０となり，大局的な測地系をもうけることが可能でこの調和条件は厳密に成立させることができる． ということですか？ 真空中なら大局的な測地系をもうけれることの証明はどのようにすればいいのでしょうか？ 疑問符ばかりで申し訳ないです．

Re: 調和条件

Yokkun さんのレス (2008/11/04(Tue) 23:18)

毎度，的外れかもしれませんが．

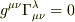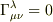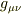g^{\mu\nu}\Gamma^\lambda_{\mu\nu}=0 は， \Gamma^\lambda_{\mu\nu}=0 とは別ですよね？ 後者は測地系でも前者はあくまで「調和座標」なのだと思ってるんですが・・・． 計量 g_{\mu\nu} に制限をつけて，弱い重力場でダランベールの方程式をあらわにするための特殊な座標系と解釈しています．重力波の伝播を示す方程式を出そうというのですから，もちろん大局的な座標系ということになるのでしょうか．トビラ．．さんの疑問符の回答にはなってませんが・・・．

Re: 調和条件

トビラ．． さんのレス (2008/11/05(Wed) 00:07)

Yokkunさんはじめまして． 回答ありがとうございます． 調和座標って初めて聞きました． つまり，計量テンソル 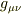g_{\mu\nu} に制約がかかった特殊な座標系ということはわかるのですが，現実的にその制約（大局的に 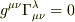g^{\mu\nu}\Gamma^\lambda_{\mu\nu}=0 ）が成り立つ計量テンソルでつくった座標系をとることは可能なのですか？

Re: 調和条件

スパイク さんのレス (2008/11/14(Fri) 18:50)

一般には，そのように出来ない（理論的に体系化されていない）ため，実際には，局地的に観測所を配備して， 内的・外的要因は別として（地球物理学として），観測が行われているのが，実態かと思われます．

例えば，

参考用URLとして： http://wwweic.eri.u-tokyo.ac.jp/mirror/index.1d.jpn.html

等があるかと思われます．