V_{12}+V_{21} =0 ?
V_{12}+V_{21} =0 ?
toorisugari no Hiro さんの書込 (2008/10/29(Wed) 13:16)
みなさんにお聞きしたいことがあります. ローレンツ変換
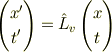
の係数を決定する際に
(1)「K系からみたK'系の空間原点の速度が  なら,K'系からみたK系の空間原点の速度は
なら,K'系からみたK系の空間原点の速度は 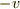 である.」
事を使います.
である.」
事を使います.
お聞きしたいのは(1)は (a) 自明 (b) 要請・仮説 (c) 他の原理(ex. 空間反転対称性)などから導かれる. のどれなのでしょう.
ガリレイ変換なら経験則からの要請(b)としても良いでしょうが,ローレンツ変換では低速の場合をのぞき経験則はありません.
ご意見をお聞かせください.
Re: V_{12}+V_{21} =0 ?
スパイク さんのレス (2008/10/29(Wed) 14:14)
Hiroさん,こんにちは.
これにつきましては,因果律との兼ね合いから仮定されている, もしくは,低速の場合から,一般に敷衍されたと解釈したほうが 宜しいかもしれません.
#取り敢えず,ご参考までですが.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/29(Wed) 15:11)
> 因果律との兼ね合いから仮定されている
ごめんなさい.意味が分かりません.もう少し説明してください.
> 低速の場合から,一般に敷衍された
高速の場合もガリレイ変換と同じと考える根拠は何でしょう. 天下りな仮説としか思えないのですが.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/29(Wed) 15:49)
(a)の自明とする方もいらっしゃると思いますが,以下のように,私にはそうは思えません. # もちろん,すごく明瞭に自明を導き出していただけることを期待して投稿してるのですが...
原点Oから正の方向に  の距離の線路上に点Aがあります.
の距離の線路上に点Aがあります.
原点Oから点Aに向けて列車が等速度で走るとき,OA間を時間 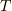 で移動したとします.このときの列車の速度
で移動したとします.このときの列車の速度  は
は 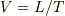 です.
です.
列車の中から観ると,点Aが負の方向に走ってくるでしょう.原点Oにいるとき,点Aまでの距離を 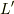 ,点Aが到着するまで時間を
,点Aが到着するまで時間を 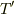 とすると,点Aの速度
とすると,点Aの速度 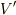 は
は 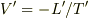 です.
です.
ご存じの通り,一般には 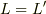 ,
, 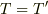 ではありません.ローレンツ変換の場合,ローレンツ収縮の比率が空間と時間で等しいので
ではありません.ローレンツ変換の場合,ローレンツ収縮の比率が空間と時間で等しいので 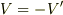 になりますが,それは結果論ですね.
になりますが,それは結果論ですね.
Re: V_{12}+V_{21} =0 ?
スパイク さんのレス (2008/10/29(Wed) 16:05)
時間が進むということと, 光速は,一定と仮定されている事から, 演繹されるのは,何かということです.
#人により,受け止め方が異なるとの,見解を得ています. *)具体的な導出は,ご自分で行われたほうが,宜しいかと思われまして;)
Re: V_{12}+V_{21} =0 ?
フジモリ さんのレス (2008/10/29(Wed) 18:20)
今晩は.ご迷惑なら無視して下さい.
(C)の相対性(慣性系の対等)に拠る,と思っていました. K(x1,t1),K'(x2,t2)とし,v12をK→K'の速度とすると, x2=γ(v12)(x1-v12*t1) 相対性により x1=γ(v21)(x2-v21*t2) x軸の正方向をそろえたとき,v12=-v21=v
Re: V_{12}+V_{21} =0 ?
DIO さんのレス (2008/10/29(Wed) 18:59)
「K系からみたK'系の空間原点が 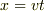 にあるとき,
にあるとき, 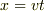 において
において  によらず
によらず 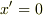 である.」
である.」
このことが言えれば良いと思うのですが,これは(1)と同じ主張なのでしょうか??
Re: V_{12}+V_{21} =0 ?
ミュフ猫 さんのレス (2008/10/29(Wed) 20:05)
K系とK'系を入れ換えても,同じ結論に達する必要があるためとか? ということは,空間の等方性を要請しているのかな?
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/29(Wed) 20:31)
> 「K系からみたK'系の空間原点が 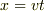 にあるとき,
にあるとき, 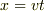 において
において  によらず
によらず 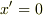 である.」
である.」
- これは「K系からみたK'系の速度が
 である.」に過ぎないのでは?
である.」に過ぎないのでは?
> 空間の等方性を要請しているのかな?
この方向に進むしかないのではと思っています.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/29(Wed) 20:48)
> この方向に進むしかないのではと思っています.
今のところ,私の立場は(c)です.
ローレンツ変換 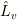 が群をなすこと,
が群をなすこと,
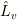 と
と  が1対1対応すること,
光速無限大の極限でローレンツ変換がガリレイ変換に漸近すること,
および,空間反転対称性.
が1対1対応すること,
光速無限大の極限でローレンツ変換がガリレイ変換に漸近すること,
および,空間反転対称性.
これらの原理から一応導き出せるのですが,ローレンツ変換を導くのと同じくらいの分量の計算になります.もっと簡単に出せるのではとおもっているのですが....
Re: V_{12}+V_{21} =0 ?
DIO さんのレス (2008/10/29(Wed) 21:02)
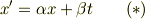
としたときに,「K系からみたK'系の空間原点が 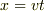 にあるとき,
にあるとき, 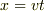 において
において  によらず
によらず 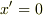 である.」が言えれば,
である.」が言えれば,
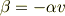
となり,
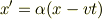
が得られます.
(1)を用いて欲しかった係数の関係とはこのことではないのでしょうか??
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/29(Wed) 21:34)
> (1)を用いて欲しかった係数の関係とはこのことではないのでしょうか??
ローレンツ変換を導出してみますね.
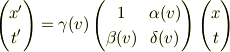
において
(1) 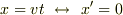 「K'系はK系に対して速度
「K'系はK系に対して速度  」
より,
」
より, 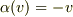 が得られます.
(2)
が得られます.
(2) 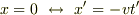 「K系はK'系に対して速度
「K系はK'系に対して速度 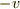 」
より,
」
より, 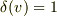 が得られます.
(3)
が得られます.
(3) 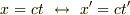 「光速は不変」
より,
「光速は不変」
より, 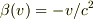 が得られます.
が得られます.
以上より,
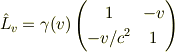
が得られ,さらに
(4) 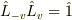 「K系はK'系に対して速度
「K系はK'系に対して速度 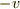 」
(5)
」
(5) 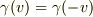 「空間反転対称性」
(6)
「空間反転対称性」
(6) 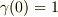 「
「 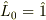 」
から
」
から 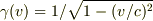 が得られ,
が得られ,
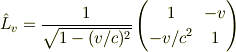
となります.
問題にしているのは(2)と(4)なのです.
Re: V_{12}+V_{21} =0 ?
yokkun831 さんのレス (2008/10/29(Wed) 22:35)
思いつきで的外れかもしれませんが・・・
はじめから反転対称な座標系を考えたらどうでしょうか? t=0において原点が一致したときに,互いに反転対称になるようなK,K'の座標系を選びます.K'のKに対する速度がvのときに,両者のスケールを一致させる選択のもとで,KのK'に対する速度が同じくvであることは対称性から確認できそうな気がします.このとき相互の変換は同じになりますから,その上でK'の座標系を反転させればvは-vになると思うのですが.
Re: V_{12}+V_{21} =0 ?
フジモリ さんのレス (2008/10/30(Thu) 00:35)
No.21939をヒントに,K→K',K'→Kを見た速度をそれぞれu,vとすると u,v対称だから f(u,v)=f(v,u)=0 f(u,v)=a(u+v)+buv=0 ? とおくと,速度に+,-の区別はないから f(u,v)=f(-u,-v)=-a(u+v)+buv=0? ?-?よりu+v=0
というのは,どうですか.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/30(Thu) 00:39)
残念ながら(1)式が出る根拠はありません. 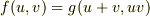 止まりです.
止まりです.
3変数でも 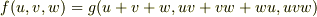 止まりですが,
仮に奇数次対称式の線形和で表現できること,
止まりですが,
仮に奇数次対称式の線形和で表現できること, 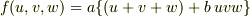 ,が出せたとしたら,
,が出せたとしたら, 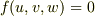 より
より 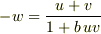 ,つまり
,つまり 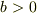 ならローレンツ変換の速度の加法則,がでるのですが,,,,そううまくはいかないでしょうね.
ならローレンツ変換の速度の加法則,がでるのですが,,,,そううまくはいかないでしょうね.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/30(Thu) 02:18)
#無意味な計算をしてたのは消しました. (#21943における元記事も消しました)
yokkun831さんの空間反転対称性のアイディアと相対性原理(慣性系によって物理法則は変わらない.)からほぼ自明に導出されるような気がしてるのですが,脳が煮えてしまったので寝ます.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/30(Thu) 14:21)
> 脳が煮えてしまったので寝ます.
相変わらず煮えたままですが,少し整理ができました.
ある慣性系 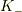 において静止している人
において静止している人 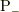 が,別の慣性系
が,別の慣性系 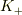 において静止している人
において静止している人 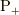 をみて,「
をみて,「 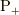 は速度
は速度  で動いている」と観測したとします.
で動いている」と観測したとします.
別の慣性系 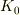 を考えます.この系で静止した観測者から
を考えます.この系で静止した観測者から 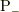 は
は 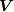 で動いているように観測され,
で動いているように観測され, 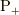 は
は 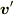 で動いているように観測されます.
で動いているように観測されます.
ここで, 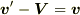 とは限りません.(cf.速度合成則)
とは限りません.(cf.速度合成則)
このとき,慣性系 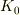 で静止した観測者は「
で静止した観測者は「 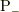 は
は 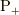 との相対速度は
との相対速度は  と観測する」と観測できるでしょうか?それともある指導原理から,そう予測できるでしょうか?ただし,ローレンツ変換やローレンツ収縮および速度合成則の内容は知らないとします.
と観測する」と観測できるでしょうか?それともある指導原理から,そう予測できるでしょうか?ただし,ローレンツ変換やローレンツ収縮および速度合成則の内容は知らないとします.
これができれば,反転対称が成り立つ系で相対速度が符号反転の関係にあることから,求める結論が得られると思うのですが...
Re: V_{12}+V_{21} =0 ?
yokkun831 さんのレス (2008/10/30(Thu) 18:30)
任意の慣性系 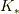 において,時空座標を
において,時空座標を 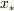 とするとき,これに対して空間座標軸を
反転させた座標系を
とするとき,これに対して空間座標軸を
反転させた座標系を 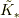 ,その時空座標を
,その時空座標を 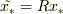 とします.ここで
とします.ここで  は,空間反転をさします.
また,
は,空間反転をさします.
また, 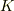 に対して速度
に対して速度  をもつ慣性系
をもつ慣性系 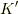 への座標変換を
への座標変換を 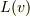 であらわします.このとき,
であらわします.このとき,
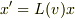
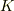 を空間座標反転させると,
を空間座標反転させると, 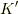 の速度は
の速度は 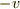 になりますから
になりますから
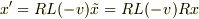 したがって,基本定理
したがって,基本定理 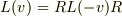 を得ます(ほぼ自明).
を得ます(ほぼ自明).
任意の慣性系の組 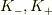 に対して,
に対して,
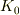 から
から 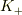 を見た速度を
を見た速度を  すなわち
すなわち 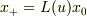
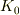 から
から 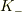 を見た速度を
を見た速度を 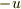 すなわち
すなわち 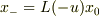 とするような
とするような 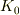 をとることができることは自明と思われます.
をとることができることは自明と思われます.
さて,
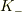 から
から 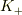 を見た速度が
を見た速度が  であることを
であることを 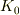 の観測者が知りえたとしましょう.このとき,
の観測者が知りえたとしましょう.このとき,
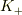 から
から 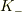 を見た速度が
を見た速度が 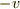 に他ならないことを同じ観測者が判定できればいいということになるでしょうか?
そして,これは
に他ならないことを同じ観測者が判定できればいいということになるでしょうか?
そして,これは
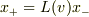 であるならば
であるならば 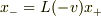 すなわち,
すなわち, 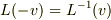 となるべきことを示せばよいということになると思います.
となるべきことを示せばよいということになると思います.
ここですべての慣性系を一斉に空間座標反転させます.
すると, 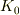 にとって
にとって 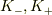 の立場が入れ替わるだけで
他に何の変化もないことは自明に思われます.これを認めれば,対称性によって
の立場が入れ替わるだけで
他に何の変化もないことは自明に思われます.これを認めれば,対称性によって
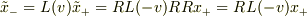 すなわち,
すなわち,
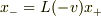 となり,目的の結果を得ました.
となり,目的の結果を得ました.
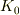 を介すべきであれば,
を介すべきであれば,
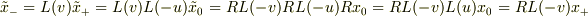 となります.
となります.
ただし,以上の考察で変換が1次変換であるということは前提となっています.
何か,記号をもてあそんだだけのような気もしないでもありません.
一斉に反転させた時点で 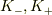 の入れ替えが起こることを認めるかどうかということだけです.
これを認めた時点で
の入れ替えが起こることを認めるかどうかということだけです.
これを認めた時点で 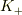 に対する
に対する 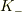 の速度を
の速度を 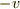 であると認めたことになりますね.
入れ替えによる対称性を認めることができれば,要するに,「自明」につきる気がします.
であると認めたことになりますね.
入れ替えによる対称性を認めることができれば,要するに,「自明」につきる気がします.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/30(Thu) 19:46)
> さて,
> 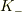 から
から 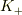 を見た速度が
を見た速度が  > であることを
> であることを 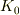 の観測者が知りえたとしましょう.このとき,
>
の観測者が知りえたとしましょう.このとき,
> 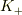 から
から 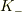 を見た速度が
を見た速度が 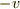 > に他ならないことを同じ観測者が判定できればいいということになるでしょうか?
> に他ならないことを同じ観測者が判定できればいいということになるでしょうか?
良いと思います.
# 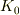 は速度だけでなく位置も中点でなければいけないと思いますが,問題ないですね.
は速度だけでなく位置も中点でなければいけないと思いますが,問題ないですね.
「反転対称性により『 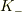 から
から 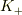 を見た速度が
を見た速度が  なら,
なら, 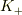 から
から 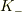 を見た速度は
を見た速度は 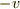 である.』と
である.』と 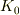 系で言明できること」
もOKだと思います.
系で言明できること」
もOKだと思います.
ただ気になるのは
(1)上の言明は 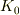 系以外の慣性系でも通用するのか?
(2)相対速度が
系以外の慣性系でも通用するのか?
(2)相対速度が  であることを
であることを 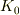 の観測者が知りえるのか?
です.
の観測者が知りえるのか?
です.
(2)が言えれば自動的に(1)は成り立ちますが,最悪「相対速度 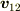 」を知り得なくても,「
」を知り得なくても,「 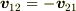 」が
」が 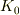 系で言えたら他の慣性系でも成り立って欲しいと思いますが,「
系で言えたら他の慣性系でも成り立って欲しいと思いますが,「 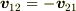 」は「物理法則」でしょうか?
」は「物理法則」でしょうか?
Re: V_{12}+V_{21} =0 ?
yokkun831 さんのレス (2008/10/30(Thu) 21:02)
># は速度だけでなく位置も中点でなければいけないと思いますが,問題ないですね.
空間の並進対称性すなわち
座標変換  は
は  のみの関数である
ことを前提とすれば,不要のような気がします.
のみの関数である
ことを前提とすれば,不要のような気がします.
>(1)上の言明は 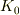 系以外の慣性系でも通用するのか?
>(2)相対速度が
系以外の慣性系でも通用するのか?
>(2)相対速度が  であることを
であることを 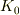 の観測者が知りえるのか?
の観測者が知りえるのか?
(1)は,同様の考察をくりかえせば任意の慣性系にたどりつける気がします. すると,残すところは(2)に集約されるように思われるのですが.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/30(Thu) 22:31)
> (1)は,同様の考察をくりかえせば任意の慣性系にたどりつける気がします.
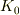 系は二つの系の「中点」である特別な系です.どう繰り返せばよいのでしょう.
系は二つの系の「中点」である特別な系です.どう繰り返せばよいのでしょう.
> すると,残すところは(2)に集約されるように思われるのですが.
うううむ....
煮詰まりましたか....ちょっと,休憩が必要でしょうか.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/31(Fri) 12:29)
式で考えてみます.相対速度を 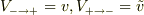 とすると,
とすると,
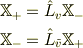
これを中点系に変換してみると,それぞれの相対速度は符号反転の関係にあるから,
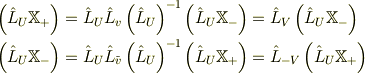
つまり
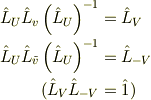
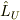 と
と 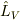 ,
, 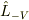 が可換なら
が可換なら

ですが,非可換のとき
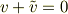
になるのかはわかりませんね....
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/31(Fri) 12:59)
No.21937の
> 今のところ,私の立場は(c)です.
> ローレンツ変換 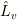 が群をなすこと,
>
が群をなすこと,
> 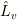 と
と  が1対1対応すること,
> 光速無限大の極限でローレンツ変換がガリレイ変換に漸近すること,
> および,空間反転対称性.
が1対1対応すること,
> 光速無限大の極限でローレンツ変換がガリレイ変換に漸近すること,
> および,空間反転対称性.
でやってみます.冗長です.
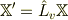
となる 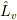 は群をなし,パラメータと1対1対応するから,
は群をなし,パラメータと1対1対応するから,
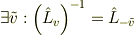
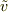 と
と  の関係を
の関係を

とすると,これは原点を通る1to1な関数である.
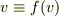 を証明したい.
を証明したい.
光速無限大の極限でローレンツ変換がガリレイ変換に漸近することにより

また,逆の逆は元に戻る( 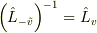 )から,
)から,

(1)(3)より
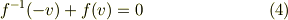
(2)(4)を同時に満たす関数のグラフ 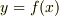 は
は 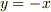 を軸にする反転対称なものなら
を軸にする反転対称なものなら  以外にも存在するので決まらない.
以外にも存在するので決まらない.
そこで,空間反転対称 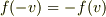 を要請する.
を要請する.

と(1)により,

(4')(2)より,一意的に
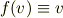
Q.E.D.
Re: V_{12}+V_{21} =0 ?
toorisugari no Hiro さんのレス (2008/10/31(Fri) 13:37)
上の記事はすごく冗長な計算になるのですが,
(1) ローレンツ変換 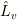 が群をなすこと,
(2)
が群をなすこと,
(2) 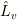 と
と  が1対1対応すること,
(3) 光速無限大の極限でローレンツ変換がガリレイ変換に漸近すること,
(4) および,空間反転対称性.
の要請をつかっていました.
が1対1対応すること,
(3) 光速無限大の極限でローレンツ変換がガリレイ変換に漸近すること,
(4) および,空間反転対称性.
の要請をつかっていました.
(1)は変換の基本的性質,(2)は系Aに対して別の系Bが与えられたら必ず相対速度 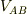 がきまること,ということで自明に近い物です.
がきまること,ということで自明に近い物です.
(3)は不要かもしれません.実際 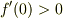 であれば十分で,これは1to1性,
であれば十分で,これは1to1性, 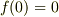 ,と併せて,
,と併せて, 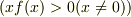 ,つまり(3')「それぞれの系からみた相対速度が逆平行」であることを要請しています.
,つまり(3')「それぞれの系からみた相対速度が逆平行」であることを要請しています.
(4)「空間反転対称性」は仮定しないと一意的にきまりません.
証明では(5)「系1の速度から系2の速度が導き出せるなら,同様の式で系2の速度から系1の速度が導き出せなければいけない.」ことも用いました.
(3')(4)(5)のなかに,すでに結論近いものがふくまれている気がします. ですから,(3')(4)(5)と結論から以下のような言明を考えました.
「二つの慣性系 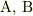 がある.系間を記述する相対的な法則は
がある.系間を記述する相対的な法則は
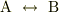 の置換操作と空間反転操作
を合わせた操作に対して不変でなければいけない.」
の置換操作と空間反転操作
を合わせた操作に対して不変でなければいけない.」
「これを要請とする」で, 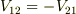 の問題は手打ちになりそうな気がします.
の問題は手打ちになりそうな気がします.
# 泰山鳴動して...という感じですね.