無題
無題
誘導起電力 さんの書込 (2008/10/28(Tue) 23:32)
東大物理の問題なんですが． (１)は自分でやってみたところなんとかできました． おそらく答えはvdbxだと思います(理由はＡＦで誘導された起電力がＢＥでの起電力に打ち消され，ＣＤの起電力のみが流れるからと思います． 間違ってたらすいません．明日までになんとか仕上げなければいけないのでできれば今日中お願いします．)
問題は次のとおりです． xyz座標をもつ空間に，z方向に向いた磁界がある． 点xyzにおけるその磁束密度は，y,zによらずxに比例し正の数bを用いてbx(Wb/m2乗)であり， 単位時間当たりr(Ω／ｍ)の抵抗をもつ導線がありはしご型回路をつくりy軸に平行にして短辺３辺ＡＦ，ＢＥ，ＣＤをとりｘ軸並行に長編ＡＣ，ＦＤをとるときＢＣ＝ＤＥ＝2dＡＢ＝ＥＦ＝ＡＦ＝ＢＥ＝ＣＤ＝ｄである
このときｘ軸方向に外力Ｆを加え引っ張ったところ，一定速度ｖで動くようになった．電磁誘導による電流の作る磁界の影響は無視できるものとする
(１)正方形ABEFAに誘導される起電力Ｖ１を求めよ．
(２)巡回路ABEFAおよび巡回路ACDEBのそれぞれに誘導される起電力Ｖ１，Ｖ２と 導線ＡＢ，ＢＣに流れる電流Ｉ１，Ｉ２との間の２つの関係式それぞれ導け また導線ＢＥを流れる電流をb d r v を用いてあらわせ
(３)もあるのですが，とりあえず(２)までお願いします．
Re: 無題
yokkun831 さんのレス (2008/10/29(Wed) 10:12)
こんにちは．とりあえず，次のような方針でいかがでしょうか？
(i) AFの位置xとするとき，AF・BE・CDに生じる起電力を 磁場を横切る導体棒に生じる起電力V=vBL の公式で求めます． (ii) V1=V(BE)-V(AF)，V2=V(CD)-V(BE)によって巡回路の起電力を得ます． (iii) キルヒホッフの法則によって，I1,I2の連立方程式をたてます． (iv) 連立方程式を解いて，I(E→B)=I2-I1 を得ます．
Re: 無題
mNeji さんのレス (2008/10/29(Wed) 12:28)
＞(１)正方形ABEFAに誘導される起電力Ｖ１を求めよ．
に付いて，別解を考えます：電磁誘導として取り扱ってみます．
在る時刻tに，点Aのx軸の位置は題意より
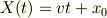
とします．此処で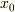 
初期位置です．また，ある地点(x,y)での磁束密度は，
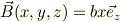
この時刻tのときに，正方形ABEFAを貫く磁束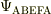 
は，
![\Psi_{\mathrm{ABEFA}} &= \int_{x=X(t)}^{x=X(t)+d}\int_{y=0}^{y=d}\vec B(x,y,z) \cdot \vec e_z \mathrm{d}x \mathrm{d}y\\&=\int_{x=X(t)}^{x=X(t)+d}bx \mathrm{d}x\int_{y=0}^{y=d} \mathrm{d}y\\&= \frac{b}{2}\left[x^2\right]_{x=X(t)}^{x=X(t)+d}\cdot d](http://hooktail.maxwell.jp/bbslog/24a5480c009e4c2f75abb367625be607.png)
により求められます．電磁誘導の式から，この時間についての偏微分が起電力となりますので，この回路の電流を出せますね．
