フジモリ さんの書込 (2008/10/28(Tue) 12:14)

直線上に3個の慣性座標系A,B,Cがあり，A→B，B→C，C→Aを見た速度がそれぞれu,v,wであるとき，それらの関係をf(u,v,w)=0とする．以下のことが成り立つだろうか． (a) f(u,v,w)=0u,v,wに成り立つ関係fを定義 (b) f(-u,-v,-w)=0速度の方向に+-の区別はないから (c) f(v,w,u)=0相対性で速度がずれても成り立つだろうから (d) f(-w,-v,-u)=0相対性でA→B→C→Aと，A→C→B→Aと見るのに区別はないから (e) f(w,v,u)=0(b)と(d)が成り立てば対称だから

皆さん，考えがあったらお聞かせ下さい．

yokkun831 さんのレス (2008/10/28(Tue) 14:15)

こんにちは．

もし，f(u,v,w)=0 がＡ，Ｂ，Ｃの速度を拘束する条件でなく，空間においてつねに成立すべき関係を表しているのならば，(a)〜(e)がすべて成立するのは自明のことのように思われます．もしそうであれば，f(u,v,w)=0は

ガリレイ変換の範囲では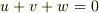， ローレンツ変換の範囲では，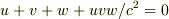

という関係をさすことになるのではないでしょうか？

フジモリ さんのレス (2008/10/29(Wed) 17:54)

今晩は．

>もし，f(u,v,w)=0 がＡ，Ｂ，Ｃの速度を拘束する条件でなく，空間においてつねに成立すべき関係を表しているのならば

はい，そうです．3個の慣性系において恒に成立する関係と考えています．但しガリレイ変換やローレンツ変換の範囲でu,v,wの具体的な関係式を知らない，という場合を想定しています．

自明のことであるために相対性以外の何らかの前提条件があるかを，考えています．

toorisugari no Hiro さんのレス (2008/10/29(Wed) 21:14)

おもしろい方向性だと思います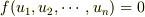． がどの2変数に対する置換に対しても対称ということを導かれたわけですね．

2変数の場合 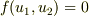が対称ということですから， は 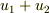, 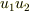の組み合わせで表現されるはずです．

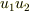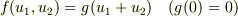何らかの原理で が から除去可能であること，つまり が示せれば，別スレッドの私の疑問も解決するのですが．．．．．

# でも，簡単ではなさそうです．

フジモリ さんのレス (2008/10/30(Thu) 11:01)

話はそれますが

>ローレンツ変換の範囲では，u+v+w+uvw/c^2=0 (No.21919 yokkun831さん)

これからc^2=-uvw/(u+v+w) となるので，直線上の3個の慣性系の相対速度を正確に測れば，原理的にはcの値が得られるということになりますが，意外です．

yokkun831 さんのレス (2008/10/30(Thu) 21:14)

>直線上の3個の慣性系の相対速度を正確に測れば，原理的にはcの値が得られるということになりますが，意外です．

「相対速度を正確に測る」には，時空の定数cが測定基準として必要であると言い換えることができると思います．