デルタ関数

デルタ関数

snow さんの書込 (2008/10/26(Sun) 22:23)

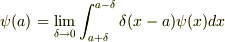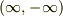すみません．次の式は成り立ちますか？ \psi(a)=\lim_{\delta \to 0}\int_{a+\delta}^{a-\delta}\delta(x-a)\psi(x)dx 積分範囲が (\infty, -\infty) なら成り立つと思うのですが，これは成り立ちますか？

Re: デルタ関数

mNeji さんのレス (2008/10/26(Sun) 23:46)

細かな話ですが，変数名を関数とダブらぬように 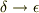\delta \to \epsilon (正の微小定数)とし，区間も逆とする；

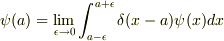
\psi(a)=\lim_{\epsilon \to 0}\int_{a-\epsilon}^{a+\epsilon}\delta(x-a)\psi(x)dx

と如何でしょうか．

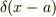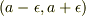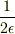それでよければ，この関数 \delta(x-a) は，区間 (a-\epsilon, a+\epsilon ) だけに，高さ \frac{1}{2\epsilon} となる関数としてイメージして宜しいのではないでしょうか．これなら普通の関数として考えていいかと...．

もちろん，高度に数学的な検討は，識者の方々にお任せしますが(笑)．

Re: デルタ関数

toorisugari no Hiro さんのレス (2008/10/27(Mon) 12:02)

> 次の式は成り立ちますか？

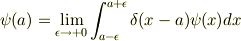
\psi(a)=\lim_{\epsilon \to +0}\int_{a-\epsilon}^{a+\epsilon}\delta(x-a)\psi(x)dx

# もとの snowさんの式は意味不明ですので，mNejiさんの式(を若干変更した式)だとします．

成り立たない，というより，上式右辺のような式が出てくること自体間違ってます．

Re: デルタ関数

snow さんのレス (2008/10/27(Mon) 18:37)

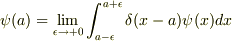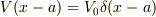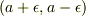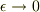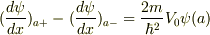すみません．積分範囲はミスです． \psi(a)=\lim_{\epsilon \to +0}\int_{a-\epsilon}^{a+\epsilon}\delta(x-a)\psi(x)dx これでお願いします． えーと，ポテンシャルが V(x-a)=V_{0}\delta(x-a) の形のとき， シュレーディンガー方程式を (a+\epsilon,a-\epsilon) で積分して， \epsilon \to 0 とすれば， (\frac{d\psi}{dx})_{a+}-(\frac{d\psi}{dx})_{a-}=\frac{2m}{\hbar^{2}}V_{0}\psi(a) となるらしいので，上の式が成り立てばこの式も成り立つと思いました．

Re: デルタ関数

toorisugari no Hiro さんのレス (2008/10/27(Mon) 19:20)

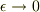> \epsilon \to 0 とすれば，

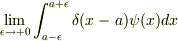これは \lim_{\epsilon \to +0}\int_{a-\epsilon}^{a+\epsilon}\delta(x-a)\psi(x)dx を考えているのではないです．

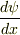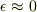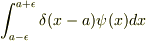強いて言えば， \epsilon は \frac{d\psi}{dx} が変化しない程度( \epsilon\approx 0 )に小さい距離 であるが， \int_{a-\epsilon}^{a+\epsilon}\delta(x-a)\psi(x)dx が意味を持つ程度( 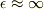\epsilon\approx\infty )には大きい距離 という感じでしょうか．

Re: デルタ関数

snow さんのレス (2008/10/27(Mon) 20:34)

ありがとうございます．わかりました． しかし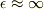， \epsilon\approx\infty というのはなんだか釈然としませんね． こういった解釈は物理では頻繁にあるのですか？

Re: デルタ関数

mNeji さんのレス (2008/10/27(Mon) 21:13)

ちょっと違う印象を持っているのでコメントします．

＞しかし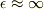， \epsilon\approx\infty というのはなんだか釈然としませんね． ＞こういった解釈は物理では頻繁にあるのですか？

私は，デルタ関数は数学的な取り扱いが明確な為に使われるのであって，物理的なイメージに目を瞑ったものだと思います．

同じ様な論議が，以前，湯川型ポテンシャルのスレッドで行われたと思います．また電磁気でも，点電荷の運動を取り扱いの便利の為にデルタ関数を記述します．

逆にいえば，今回の場合でも，非常に狭い領域に，高い障壁をもったポテンシャルがあった時の量子力学的振る舞いが問題となっているとすれば，考え易いのではないでしょうか．

Re: デルタ関数

toorisugari no Hiro さんのレス (2008/10/28(Tue) 12:28)

> こういった解釈は物理では頻繁にあるのですか？

スケールの分離という物理で頻繁に出る考え方です．

連続体としての水を考えます．ある位置 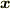\bm{x} における水の密度を計算するとき，その点を重心とする体積 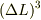(\Delta L)^3 の立方体に含まれる質量 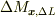\Delta M_{\bm{x},\Delta L} から

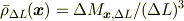
\bar \rho_{\Delta L}(\bm{x}) = \Delta M_{\bm{x},\Delta L}/(\Delta L)^3

という計算をすると思います．

しかし，密度が非一様のときはこの値は平均近似でしかありません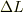． \Delta L に依存するからです．そこで，普通

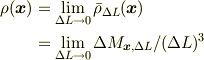
\rho(\bm{x}) &= \lim_{\Delta L\to 0}\bar \rho_{\Delta L}(\bm{x})\\&= \lim_{\Delta L\to 0} \Delta M_{\bm{x},\Delta L}/(\Delta L)^3

と，「極限」あるいは「微分」を使って密度を定義するはずです．

でも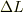，「 \Delta L が0の極限」を考えるのですが，これは実際の水において大丈夫でしょうか?実際の水は水分子からなる離散的な存在です．ですから， \lim_{\Delta L\to 0}\bar \rho_{\Delta L}(\bm{x}) は連続体としての密度に「収束」しません．

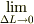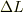そこで物理においては \lim_{\Delta L\to 0} を以下のように解釈をします． 「 \Delta L は巨視的状態量が変化する空間スケールより遙かに小さいが，分子系の特徴的なスケール(平均自由行程，分子間距離)にくらべて遙かに大きい．」 逆に，これができない(巨視的スケールと微視的スケールが分離できない)とき，水は「連続体」とは見なせません．

以上は物理の話で，問題になっているのは数学ですから説明になっていないのかもしれません．

しかし，本来 \delta 関数は

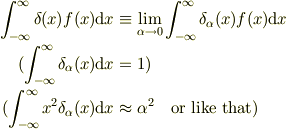
\int_{-\infty}^{\infty}\delta(x)f(x) \mathrm{d}x &\equiv \lim_{\alpha \to 0}\int_{-\infty}^{\infty} \delta_\alpha(x) f(x) \mathrm{d}x \\(\int_{-\infty}^{\infty} \delta_\alpha(x) \mathrm{d}x &= 1)\\(\int_{-\infty}^{\infty} x^2 \delta_\alpha(x) \mathrm{d}x &\approx \alpha^2 \quad \text{or like that})

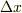で定義される幅を持つ分布です．(ここで \alpha の極限は「幅を0にすること」ではなく「幅 \alpha は十分小さい」と解釈するべきです．) ですから， \delta 関数を含む計算で極限操作を行うときは 「 \Delta x は関数が変化するスケールより遙かに小さいが， \delta 関数が定義されるスケール \alpha にくらべて遙かに大きい．」ということ頭に入れておかないといけません．

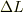\delta 関数を点電荷に結びつけることが多いですが， \delta 関数を扱う場合，点電荷は大きさを持たない電荷というより，「有限の広がりを持つ電荷分布を十分大きなスケールから観たもの」です．ですから 「 \Delta L は場が変化するスケールより遙かに小さいが，電荷分布の拡がりにくらべて遙かに大きい」ようなスケールを使って微分(ex. Laplacian)を定義すると，必然的に \delta 関数が現れてきます．

Re: デルタ関数

snow さんのレス (2008/10/28(Tue) 18:52)

なるほど．非常にわかりやすかったです． 本当にありがとうございます．