電磁気学についてです.
電磁気学についてです.
りこ さんの書込 (2008/10/21(Tue) 00:08)
初めまして. 大学2年生のりこです.
自分で考えてみたのですが,,合っているのか,,,, という状態です.
どなたか意見や添削のコメントお願いします..
合っている自信はありません..
問.原点を中心にして電荷が球対称に分布している.ただし密度は一様ではなく半径rにおける電荷密度はρ(X)=ρ0/rと表される.このとき,半径rにおける電場の大きさをrの関数で表しなさい.
どうかよろしくお願いします..
Re: 電磁気学についてです.
mNeji さんのレス (2008/10/21(Tue) 07:47)
りこさん,初めまして.
自分で問題を考え出すのは,とても良い勉強方法の一つと思います.でも,その為には,その問題を自分で解かないと,効果は半減どころか,1/10位かとおもいます.
さて,問題として拝見すると,概略は判ります.しかし「X」とは何でしょうか.出題する場合,(x,y,z)とか tとか mや gなど,慣例で使われる変数として無定義で使用するのは避けるべきと思います.
是非とも,ご自分の解もお書きになってくださいね.
Re: 電磁気学についてです.
りこ さんのレス (2008/10/21(Tue) 09:39)
ご返事ありがとうございます. すいません! あたしの書き方が悪かったのか,答案を載せなかったのが悪いのか,,
けっして自分で考えたわけではないです.
すいません.
ρ(x)というある関数ではないですかね?
それがρ0/rていうことではないかと..
自分の答案載せます.
クーロンの法則より E=1/4πε0∬∫v[ρ(r')dv]/R^2 球対称なので
=4πR^2/4πε0R^2∫ρ0/r dr
=ρ0/ε0∫1/rdr
まで解けました.
あってますかね?
Re: 電磁気学についてです.
mNeji さんのレス (2008/10/21(Tue) 10:11)
>ρ(x)というある関数ではないですかね? >それがρ0/rていうことではないかと..
では,この xは何でしょう?
>クーロンの法則より >E=1/4πε0∬∫v[ρ(r')dv]/R^2
「クーロンの法則」からと言うのもあるとは思いますが,それならそれで表現が異なるとおもいます.
さらに,「v」「r'」「R」とは何ですか?
また積分の範囲はどうなのでしょうか?
そもそも,本来の問題を明示しないと,論議が収束しないようにも感じます.
Re: 電磁気学についてです.
りこ さんのレス (2008/10/21(Tue) 11:27)
なかなか難しいですね.
問題文はすべて載せました..
xってなんでしょうね. 距離の関数ですかね?
電荷密度が一様なら簡単なんでしょうね.
なんかこんがらがってきました.
クーロンの法則をなんらかの形で使いますよね?
教科書に載っていた クーロンの法則から 分布電荷の作る電場
E=1/4πε0∫∫∫v[ρ(r')dv']/R^2 を使おうと考えました.
r'は原点からある立方体【体積v'】までの距離でRは測定したいP点までの距離です.
Re: 電磁気学についてです.
mNeji さんのレス (2008/10/21(Tue) 12:49)
>問題文はすべて載せました..
となると失礼ながら,その問題は判らん状態ですね.
>xってなんでしょうね. >距離の関数ですかね?
簡単な数学で2次式を考えるとき,独立変数 xとして,関数 f(x)を次に定義する;
f(x) = ax^2 +bx +c
ここで,a,b,c は定数で,とくに aはゼロでないとする.
といったら,その関数は意味をもちますね.でも仮に,
f(x) = ar^2 +br +c
と書いたら,どうなるのでしょうか.
>クーロンの法則をなんらかの形で使いますよね?
ある意味では,正解です.でも「クーロンの法則」から出発すると,腕力仕事になるのも事実でしょう.
>教科書に載っていた >クーロンの法則から >分布電荷の作る電場
というと,「電荷が存在する領域のサイズ」と「電場を観測する距離」とになんらかの仮定があるような気がします.
>E=1/4πε0∫∫∫v[ρ(r')dv']/R^2
ヒョッットして,
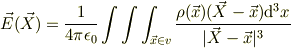
ここで, 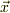 は,原点から見た電荷のある所の位置ヴェクタ.
また,
は,原点から見た電荷のある所の位置ヴェクタ.
また, 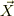 は,原点から見た考察点の位置ヴェクタ.
は,原点から見た考察点の位置ヴェクタ.
 は,電荷分布の存在体積領域.
は,電荷分布の存在体積領域.
とかかも知れませんね.これに電荷分布の対称性や局所性を考慮して計算しようとするとか....
Re: 電磁気学についてです.
りこ さんのレス (2008/10/21(Tue) 13:20)
今先生にききにいったら,xではなくてrだそうです! 一つ解決です.
んー私には難しいですね..
その記号や文字の文は.. すいません.
Re: 電磁気学についてです.
mNeji さんのレス (2008/10/21(Tue) 13:34)
先に書いたのは,推測が強すぎるので修正します,ご免なさい.
今日,細切れに検討しましたが,出題者の方に質問されるのが一番だと思う様になりました.
逆に,判ったら,教えて戴けると幸いです.
Re: 電磁気学についてです.
りこ さんのレス (2008/10/22(Wed) 11:42)
一応自分で解いてみました. はじめ言ってたのとはちがうやりかたですけど,,,
密度ρ(r)=ρ_0/rにおける全電荷をqとする. q=∫ρ(r)dv
q=∫∫∫ρ_0/r(r^2sinθdrdθdφ)
【dr:0〜r,dθ:0〜π,dφ:0〜2π】
q=2ρ_0πr^2
これを E=q/4πεr^2に代入して
E=ρ_0/2ε
となりました..
何度もすいませんが意見お願いします!
Re: 電磁気学についてです.
toorisugari no Hiro さんのレス (2008/10/22(Wed) 12:14)
ガウスの法則
「閉曲面を横切る電気力線の本数 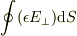 は内部の電荷量
は内部の電荷量 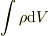 に等しい」
を球対称性を考慮して球面に対して適用したものですね.
に等しい」
を球対称性を考慮して球面に対して適用したものですね.
正しいと思います.
Re: 電磁気学についてです.
yokkun831 さんのレス (2008/10/22(Wed) 12:49)
こんにちは.横から失礼します.
球対称な電荷分布なので,球殻について和をとればよく
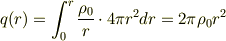
ですね?余計なお世話っぽいですが.^^;
Re: 電磁気学についてです.
mNeji さんのレス (2008/10/22(Wed) 12:50)
>はじめ言ってたのとはちがうやりかたですけど,,,
ちなみに,「ガウスの法則」とか「積分形のガウスの法則」と呼ばれる式に,球対称性を適用した式をご利用になったのだと思います.
>密度ρ(r)=ρ_0/rにおける全電荷をqとする. >q=∫ρ(r)dv
この場合,半径rの球内部の電荷をq(r)とすると, q(r)=∫ρ(r)dv とするか,ある半径Rまでで,電荷分布が途切れるとするかなどの可能性がありますね.
Re: 電磁気学についてです.
りこ さんのレス (2008/10/22(Wed) 18:36)
電荷分布が途切れるってどういうことですか?
Re: 電磁気学についてです.
toorisugari no Hiro さんのレス (2008/10/22(Wed) 18:54)
> いろんなやり方があるんですねぇ.
いや,おなじ事.:-)
球対称な分布なら
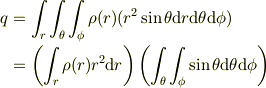
に対して立体角の公式
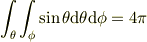
を適用した
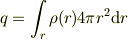
から始めるのが定石だというアドバイスです.
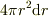 が厚さ
が厚さ 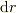 の球殻ですよね.
の球殻ですよね.
Re: 電磁気学についてです.
mNeji さんのレス (2008/10/22(Wed) 23:08)
>電荷分布が途切れるってどういうことですか?
ご自分でも計算されている様に,半径rの内部に入っている電荷量,q(r)はr^2に比例しますから,無限遠方で発散しますね.それが気になったので,r>=Rでは,q(r)=0とでもするとどうかと思っただけです.
もしもそうだとすると,全電荷量をQとすると,
Q = q(R) = 2πρ_0*R^2
従って,
q(r) = Q*(r/R)^2
となって,如何にもq(r)の次元が電荷であるのがはっきりしますよね.