一般化座標
一般化座標
digi さんの書込 (2008/10/19(Sun) 22:11)
N個の質点があるとき,デカルト座標 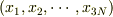 と一般化座標
と一般化座標 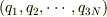 の間には変換関係
の間には変換関係
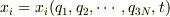 (1)
(1)
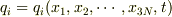 (2)
があると解析力学の本で読みました.デカルト座標と極座標で考えてみると,j番目の質点のx座標は
(2)
があると解析力学の本で読みました.デカルト座標と極座標で考えてみると,j番目の質点のx座標は
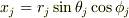 だから,j番目の質点のデカルト座標
だから,j番目の質点のデカルト座標 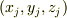 に影響するのはj番目の質点の極座標
に影響するのはj番目の質点の極座標 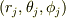 の3つだけで,他の質点の座標には影響を受けないように思うのですが.一般化座標の場合は違うのでしょうか?
の3つだけで,他の質点の座標には影響を受けないように思うのですが.一般化座標の場合は違うのでしょうか?
あと,(1)のように書いたとき, 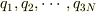 は時間の関数なのでしょうか?
は時間の関数なのでしょうか?
Re: 一般化座標
toorisugari no Hiro さんのレス (2008/10/20(Mon) 14:40)
> 他の質点の座標には影響を受けないように思うのですが.一般化座標の場合は違うのでしょうか?
重心系はご存じですか?
> あと,(1)のように書いたとき, |a51d9b0f30b2aca0c0b539944e7a10c8| は時間の関数なのでしょうか?
座標原点が等速度で動く場合や回転座標系はご存じですか?
Re: 一般化座標
digi さんのレス (2008/10/21(Tue) 23:07)
>重心系はご存じですか?
全質点の重心が座標原点にある系ですよね?重心系だと
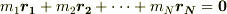 となって,デカルト座標だとx成分は
となって,デカルト座標だとx成分は
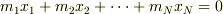 となると思います.ここから,デカルト座標と一般化座標との変換関係を求めるにはどうすればいいのでしょうか?
となると思います.ここから,デカルト座標と一般化座標との変換関係を求めるにはどうすればいいのでしょうか? 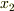 〜
〜 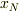 を
を 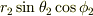 〜
〜 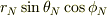 とすれば,
とすれば, 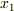 が分かると思いますが.
が分かると思いますが.
>座標原点が等速度で動く場合や回転座標系はご存じですか? 座標系が時間的に変化するから,質点の座標も時間に依存するということですね. ハミルトン力学形式では一般化座標と一般化運動量と時間は独立変数としていますが,この場合は,一般化座標が時間に依存しないのではないでしょうか?
Re: 一般化座標
toorisugari no Hiro さんのレス (2008/10/22(Wed) 12:27)
>> 重心系はご存じですか?
> この場合は,一般化座標が時間に依存しないのではないでしょうか?
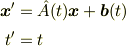
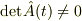 なら
なら 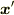 と
と 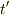 は独立です.
は独立です.
Re: 一般化座標
digi さんのレス (2008/10/24(Fri) 02:05)
返事が遅れて申し訳ありません.
>>> 重心系はご存じですか?
全質点の重心が座標原点にある系ではないのですか?
> |d4271dacf60c7aaa7fbdaf2b4648f945|
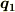 が一般化座標ですか?
が一般化座標ですか?
Re: 一般化座標
toorisugari no Hiro さんのレス (2008/10/24(Fri) 11:54)
> 全質点の重心が座標原点にある系ではないのですか?
もちろんそうです.ただ,重心からの変位( 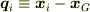 )のみの座標系で記述すると,その系での重心座標は定義により0(
)のみの座標系で記述すると,その系での重心座標は定義により0( 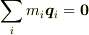 )ですから,自由度は一個減ります.適当な粒子の変位(たとえば
)ですから,自由度は一個減ります.適当な粒子の変位(たとえば 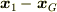 )と元の系での重心の位置(
)と元の系での重心の位置( 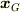 )を入れ替えた組(
)を入れ替えた組( 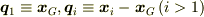 )を考えると,自由度は元に戻り ,一般化座標系
)を考えると,自由度は元に戻り ,一般化座標系 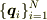 が得られますね.
が得られますね.
Re: 一般化座標
digi さんのレス (2008/10/24(Fri) 22:34)
ありがとうございました!
Re: 一般化座標
mNeji さんのレス (2008/10/24(Fri) 23:39)
横から失礼します.
多質点系でのお話は完了したと思うので,2質点系の場合をコメントさせて頂きます.
この場合,適当な慣性座標系での位置ヴェクタ 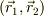 から重心のヴェクタ
から重心のヴェクタ 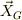 と相対のヴェクタ
と相対のヴェクタ 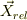 賭する事もありますね.
賭する事もありますね.
衝突問題にはこの方が運動方程式の取り扱いが直感的になるからだ,と思います.
Re: 一般化座標
yama さんのレス (2008/10/25(Sat) 00:36)
私も横から失礼します. 一般化座標が多数の質点の座標に関係する例としては,多自由度の振動を扱うときの基準座標もあります. 基準座標を用いると,多自由度の振動を,自由度と同じ個数の互いに独立な運動方程式で記述することができます. 詳しくは力学のテキストを参照してください.