解法を教えてください

サイゴンさんの書込 (2008/10/14(Tue) 21:19)

長さl，質量ｍの真っ直ぐで一様な棒が水平面上に立っている．接地点を中心として鉛直内を回転して水平面に倒れる．接地する瞬間の角速度ωを求めよ．棒の太さや摩擦，空気抵抗は無視せよ．重力加速度をｇとする．

接地点は固定されているのですか?

はい，固定されています．

それでは，エネルギー保存則で解けばいいと思います．倒れる前の重心の位置エネルギーと床に倒れる直前の接地点まわりの回転運動のエネルギーが等しいとします．あとはご自分でできるところまで考えてください．

ありがとうございます！位置エネルギーがmgl/2,回転運動のエネルギーがIω^2 (I=ML^2/3) として計算します．もし間違っていたら教えていただけると嬉しいです．

ええっと，回転運動のあたりが違うように思いますが，調べる時間がないので，他の方，フォローお願いします．

あ，1/2を抜かしていました． 1/2・Iω~2です．

横から失礼します．

多分，サイゴンさんの最初の式で良いでしょう．

検算すると；

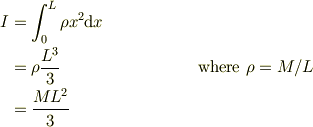
$I &=\int_0^L \rho x^2 \mathrm{d}x\\&= \rho \frac{L^3}{3} & \qquad \text{where } \rho = M/L\\&=\frac{ML^2}{3}$

教訓：指数と係数が接近する時は，間違え易いので注意 △I=ML^2/3 ○I=(ML^2)/3

恐らく ×I=ML^(2/3) と誤認され易いと思います．

ありがとうございます．助かります．