変分原理
変分原理
snow さんの書込 (2008/10/14(Tue) 17:33)
重さのある糸の両端を固定して吊るしたときの糸の形を変分原理を用いて求めるっていう問題があるのですが,解答を見ても意味が分かりません.
解答には,
ポテンシャル
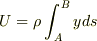 糸の長さ
糸の長さ
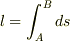 ラグランジュの未定係数法を用い,
ラグランジュの未定係数法を用い,
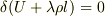 とおくと,
とおくと,
![y=-\lambda+\frac{1}{c}cosh[c(x-a)]](http://hooktail.maxwell.jp/bbslog/3e1f3b2a3ba1e0e6fbf3fad62c0dd60e.png) となるって書いてあります.
となるって書いてあります.
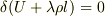 から
から ![y=-\lambda+\frac{1}{c}cosh[c(x-a)]](http://hooktail.maxwell.jp/bbslog/3e1f3b2a3ba1e0e6fbf3fad62c0dd60e.png) を出す際の詳しい解説をだれかお願いします.
を出す際の詳しい解説をだれかお願いします.
Re: 変分原理
toorisugari no Hiro さんのレス (2008/10/14(Tue) 19:03)
を
の様な形にして解けばいいのです(ピタゴラスの定理は知ってますね).
計算はややこしいですが,まずはできるところまで自力でやりましょう.
Re: 変分原理
snow さんのレス (2008/10/14(Tue) 22:13)
えーと,
![ds=\sqrt[]{\mathstrut 1+(\frac{dy}{dx})^2}dx](http://hooktail.maxwell.jp/bbslog/4821c99aa357805ab6b67154d448777e.png) となるので,
となるので,
![\delta\int(y+\lambda)\sqrt[]{\mathstrut 1+(\frac{dy}{dx})^2}dx=0](http://hooktail.maxwell.jp/bbslog/36a36b16f9e9f70e8f6c962063feea48.png) 変分すると,
変分すると,
![\int dx\frac{\frac{dy}{dx}}{\sqrt[]{\mathstrut 1+(\frac{dy}{dx})^2}}(y+\lambda)\delta(\frac{dy}{dx})=0](http://hooktail.maxwell.jp/bbslog/7ac2ba20198c4205039a11b9089bac19.png) となると思います.
ここまではあってますか?
この後どうすればよいかわかりませんでした.
となると思います.
ここまではあってますか?
この後どうすればよいかわかりませんでした.
Re: 変分原理
toorisugari no Hiro さんのレス (2008/10/14(Tue) 22:49)
に対するEuler-Lagrange方程式はご存じですか
Re: 変分原理
mNeji さんのレス (2008/10/15(Wed) 10:40)
肝心のyについての変分δyが抜けていませんか?
またδ(dy/dx)=d(δy)/dxである点に留意して,部分積分するとどうなんでしょうか.
Re: 変分原理
snow さんのレス (2008/10/16(Thu) 00:06)
Hiroさん,ありがとうございます.
Euler-Lagrange方程式を用いて出すことができました.
しかし,ひとつ疑問があります.
僕の出した解は
![y=-\lambda+\frac{1}{c}cosh[c(x+a)]](http://hooktail.maxwell.jp/bbslog/eb8247bd00947fbd7204df496b6f1a95.png) となりましたが,解答では
となりましたが,解答では 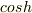 の中の
の中の  が負になっています.
意図的に負にしているように思えるのですが,何か意味があるのでしょうか?
あと,
>肝心のyについての変分δyが抜けていませんか?
あ,そうですね.つまり,
が負になっています.
意図的に負にしているように思えるのですが,何か意味があるのでしょうか?
あと,
>肝心のyについての変分δyが抜けていませんか?
あ,そうですね.つまり,
![\int dx[\frac{\frac{dy}{dx}}{\sqrt[]{\mathstrut 1+(\frac{dy}{dx})^2}}(y+\lambda)\delta(\frac{dy}{dx})+\sqrt[]{\mathstrut 1+(\frac{dy}{dx})^2}\delta y]=0](http://hooktail.maxwell.jp/bbslog/e24c2311ce392173de638b66fe528e15.png) ですね.ありがとうございます.
これを部分積分してみましたが,うまくいきません.
これでうまく解くにはどうすれば良いのでしょうか?
ですね.ありがとうございます.
これを部分積分してみましたが,うまくいきません.
これでうまく解くにはどうすれば良いのでしょうか?
Re: 変分原理
toorisugari no Hiro さんのレス (2008/10/16(Thu) 12:55)
> これを部分積分してみましたが,うまくいきません. > これでうまく解くにはどうすれば良いのでしょうか?
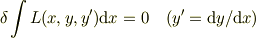
からEuler-Lagrange方程式
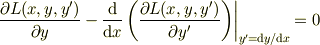
を導いてください.
> 意図的に負にしているように思えるのですが,何か意味があるのでしょうか?
問題の全体が見えないのでコメントできません.多分,境界条件や拘束条件のからみでしょう.
Re: 変分原理
mNeji さんのレス (2008/10/17(Fri) 23:12)
>これを部分積分してみましたが,うまくいきません. >これでうまく解くにはどうすれば良いのでしょうか?
という事と,
>Euler-Lagrange方程式を用いて出すことができました.
とが同時に出て来るのが自分には良く判りません.むしろ,特定な場合の部分積分ですが,Euler-Lagrange方程式を導くのと等価だと思います.従って,別々の論議は無意味だと思うので,私のコメントは,これで終了させて頂きます.
Re: 変分原理
snow さんのレス (2008/10/18(Sat) 00:37)
すみません.解析力学を全く理解していませんでした. Euler-Lagrange方程式は変分から導くものだから,僕の質問はおかしいですね. 今までEuler-Lagrange方程式を考えもせずに使っていました. 本当にすみません.
Re: 変分原理
mNeji さんのレス (2008/10/18(Sat) 07:29)
若い頃の自分も同類だったと思います.でも,
>Euler-Lagrange方程式は変分から導くものだから,僕の質問はおかしいですね.
このような点に気づかれると,ラグランジュ形式の運動方程式が身に付く段階に至ったのだと思います.
たまには古風に,ニュートン形式で解くのもおつですが....