ken さんの書込 (2008/10/11(Sat) 16:46)

流体の運動方程式について質問です． 円柱座標（r,θ,z）においての流体の運動方程式なんですが，自分のもらったテキストでは，

ρ{∂v/∂t + (v・∇)v}＝−∇p + μ∇^2v・・・・・? （ρ：密度，v：速度ベクトル，p：圧力，μ：粘性係数）

と書いてあり，これからr,θ,z方向の運動方程式をそれぞれ導くという証明が記述されているのですが，その計算過程において， (v・∇)v＝{v(r)・∂/∂r + v(θ)・∂/r∂θ + v(z)・∂/∂z}・{（v(r)e(r) + v(θ)e(θ) +v(z)e(z)}・・・・・? （v(r),v(θ),v(z)：r,θ,z方向の速度成分，e(r),e(θ),e(z)：r,θ,z方向の単位ベクトル） となっていました．

しかし，実際に(v・∇)を自分で計算したところ， (v・∇)＝{∂v(r)/∂r + v(r)/r + ∂v(θ)/r∂θ + ∂v(z)/∂z}・・・・・? となりました． 他の文献等を参照してみても，?は合っているようでした．

それで，?を?に代入して左辺の対流項を計算してみたところ結果が合いませんでした．

どこまでが合っているのかさっぱりです． また，テキストでは?の左辺において {v(r)・∂/∂r + v(θ)・∂/r∂r + v(z)・∂/∂z} というように偏微分の記号の前にv(r),v(θ),v(z)が出ていますが， (v・∇)を計算したら結果（?）から推測すると∂v(r)/∂r，∂v(θ)/∂θ，∂v(z)/∂zのようになるはずだと思います． それが前にでているということはv(r)はrの関数ではなく,v(θ)はθの関数ではなく,v(z)はzの関数ではないということでししょうか？ それとも微分演算子の計算の特殊な性質でしょうか？

長くなって申し訳ありませんが，解答をお願いします．

yokkun831 さんのレス (2008/10/11(Sat) 17:55)

∇などの演算子は，被演算関数に前置するのがルールです．したがって， （ｖ・∇）＝v(r)・∂/∂r + v(θ)・∂/r∂θ + v(z)・∂/∂z は，まだ実行されていない演算子です．ｖとの内積でスカラー演算子 に変わったところで，後置したベクトルｖにあらためて作用するわけ です．したがって，当然（ｖ・∇）≠（∇・ｖ）です．左辺はスカラー 演算子，右辺はスカラー量ですね．

ken さんのレス (2008/10/11(Sat) 18:36)

迅速な解答ありがとうございます． とてもよく理解できました．

ということは， v(r)・∂/∂r + v(θ)・∂/r∂θ + v(z)・∂/∂z＝? ということですね．

では(v・∇)vを計算する場合は?にしてからｖをかけるのと v(r)・∂/∂r + v(θ)・∂/r∂θ + v(z)・∂/∂zの状態で（単位ベクトルの内積計算のみをした状態）vをかけるのとどっちが楽でしょうか？？ またどっちが楽とかの見分け方はありますか？？

yokkun831 さんのレス (2008/10/11(Sat) 18:49)

>v(r)・∂/∂r + v(θ)・∂/r∂θ + v(z)・∂/∂z＝? >ということですね．

ちがいます．?は（∇・ｖ）ですよね？ もう一度確認すると， （∇・ｖ）はベクトル演算子∇とベクトル量ｖの内積 ｖをベクトル場とすると発散（div）になります． （ｖ・∇）はベクトルｖと∇の内積ですが，演算子に 限り交換法則は成り立たないのです．こちらは，まだ ∇が実行されません．

ken さんのレス (2008/10/11(Sat) 19:21)

なるほど．ありがとうございます．

では，（ｖ・∇）≠（∇・ｖ）ですが，これらと内積をvを右側にしてとると等しくなりますよね？？ つまり，（ｖ・∇）v＝（∇・ｖ）vは成立しますよね？？

また，（ｖ・∇）v＝v（∇・ｖ）も成立しますよね？？

もっと一般的にa,bをベクトルとすると， （a・∇）・b≠b・（∇・a）となりますか？ 左辺では偏微分はbに適用されますが，右辺ではaに適用されるのでという考えでよろしいでしょうか？？

toorisugari no Hiro さんのレス (2008/10/11(Sat) 19:28)

横から失礼．

>（ｖ・∇）v＝（∇・ｖ）vは成立しますよね？？ >（ｖ・∇）v＝v（∇・ｖ）も成立しますよね？？

しません．

yokkun831 さんのレス (2008/10/11(Sat) 19:44)

>（a・∇）・b≠b・（∇・a）となりますか？ >左辺では偏微分はbに適用されますが，右辺ではaに適用されるのでという考えでよろしいでしょうか？？

細かくなりますが，（a・∇）はスカラー演算子になるので，bとの間の「・」 はつけるべきではありません．スカラーとベクトルの内積は定義できません． 右辺も同じです．積をわかりやすくするためにつけたということであれば， 聞き捨ててください．

後半はその通りです． ちなみに，b（∇・a）＝（∇・a）b は成立します．∇のaに対する作用が 閉じているからです．（∇・a）はスカラーになりますから，ベクトルbとの 単純な積を意味します．

toorisugari no Hiro さんのレス (2008/10/11(Sat) 19:58)

横から失礼2回目．

>>（ｖ・∇）v＝（∇・ｖ）vは成立しますよね？？ >>（ｖ・∇）v＝v（∇・ｖ）も成立しますよね？？ >しません．

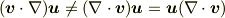
となるのは

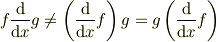
と同じ理由．

ken さんのレス (2008/10/11(Sat) 20:17)

＞yokkun831さん 細かい指摘までありがとうございます． 微分演算子についてかなり理解が深まりました． ありがとうございました．

＞toorisugari no Hiroさん レスありがとうございます． （ｖ・∇）v＝（∇・ｖ）v （ｖ・∇）v＝v（∇・ｖ） の２式はともにu,vの２種類のベクトルではなく，vというベクトル１種類のみで構成されているので成立するではないでしょうか？？ 例で挙げられたものでいうと，f＝gとなっているので．

toorisugari no Hiro さんのレス (2008/10/11(Sat) 20:25)

> ２式はともにu,vの２種類のベクトルではなく，vというベクトル１種類のみで構成されているので成立するではないでしょうか？？

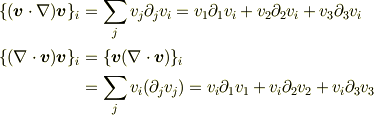
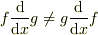ですから，よって成り立ちません．

大学２年生 さんのレス (2008/10/14(Tue) 17:40)

＞toorisugari no Hiroさん 手を動かして計算したら理解できました． ありがとうございました．