一次元の調和振動子
一次元の調和振動子
snow さんの書込 (2008/10/05(Sun) 17:09)
一次元の調和振動子のシュレーディンガー方程式を変形して
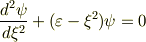
となった後に  が小さいので無視して,
が小さいので無視して,
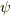 は漸近的に
は漸近的に 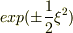 の解を持つらしいのですが,その理由がわかりません.
普通に解くと
の解を持つらしいのですが,その理由がわかりません.
普通に解くと 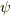 は
は 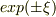 を解に持つのでは・・・.
を解に持つのでは・・・.
Re: 一次元の調和振動子
なんとなく さんのレス (2008/10/05(Sun) 18:25)
勘違いでしょう.ε<<1として無視すると, d^2ψ/dξ^2-ξ^2ψ=0・・・? ですが,ξは(従属)変数であり,定数ではありません.exp(±1/2ξ^2)は代入してみれば,解であることが分かります(一方,exp(±ξ)は解ではありません). >普通に解く・・・は,線形微分方程式の解法(公式)のことでしょうが,?は非線形ですので,公式は使えません.
Re: 一次元の調和振動子
snow さんのレス (2008/10/05(Sun) 18:54)
あ,本当だ. あほな質問してすみません.
Re: 一次元の調和振動子
toorisugari no Hiro さんのレス (2008/10/06(Mon) 12:29)
> exp(±1/2ξ^2)は代入してみれば,解であることが分かります
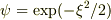 に対して,一階微分は
に対して,一階微分は 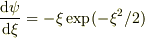 ですが,二階微分は
ですが,二階微分は 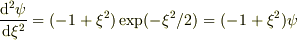 となり,解にはなりません.
となり,解にはなりません.
しかし,遠方では 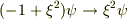 と見なせるので,
と見なせるので,
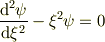
は漸近的に 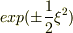 の解を持つといえます.
の解を持つといえます.