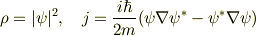波動関数の連続性
波動関数の連続性
snow さんの書込 (2008/10/04(Sat) 14:26)
ポテンシャル 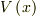 が
が 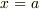 で不連続性を持つときに
波動関数
で不連続性を持つときに
波動関数 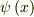 とその導関数が連続になる理由がわかりません.
教えてください.お願いします.
とその導関数が連続になる理由がわかりません.
教えてください.お願いします.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/06(Mon) 20:20)
「
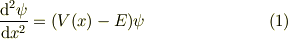
ただし, 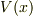 は
は 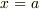 で不連続
」
という問題を解くとき,
で不連続
」
という問題を解くとき, 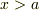 と
と 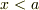 の領域で,区分的に解き,不定の定数を,
の領域で,区分的に解き,不定の定数を, 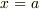 で
で 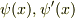 が連続として決定するという解法は定番ですが,
が連続として決定するという解法は定番ですが,
何故, 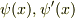 が連続としていいのか,えっと,これは私もよくわかっていません.
が連続としていいのか,えっと,これは私もよくわかっていません.
仮に波動関数 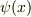 が連続なら(これは有界を含みます),
が連続なら(これは有界を含みます), 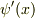 が連続であるのは,(1)式を
が連続であるのは,(1)式を 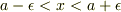 で積分すれば,以下のように導けます.(1)を積分すると
で積分すれば,以下のように導けます.(1)を積分すると
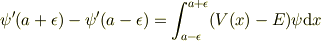
となり,右辺の被積分関数は有界ですから, 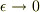 で右辺は0になり,微分の連続性は導かれます.
で右辺は0になり,微分の連続性は導かれます.
波動関数 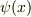 が連続(有界)であることは,物理的にどのような要請からでるのかがわかりませんので,後は識者にゆだねます.
が連続(有界)であることは,物理的にどのような要請からでるのかがわかりませんので,後は識者にゆだねます.
Re: 波動関数の連続性
スパイク さんのレス (2008/10/06(Mon) 21:16)
識者ではありませんのが;) これは,連続体仮説に基づいた論法であったように 記憶しています.なお, 連続体仮説は,未だ証明されていないかと思われます. 常識的に鑑みて,扱いやすいということではないかと思われます. #必要であれば,ブログをご参照下さい.
Re: 波動関数の連続性
yama さんのレス (2008/10/06(Mon) 22:48)
連続体仮説って?ご冗談でしょう,スパイクさん.
波動関数とその勾配の連続性は,確率の流れの密度の連続性に基づいています. 確率の流れの密度が連続でなければならないのは,そうでないと確率の流れの密度の不連続点(3次元の場合は不連続面)で確率の流れに湧き出しや吸い込みがあることになるからです. 詳しくは,適当な量子力学の本を参照してください.
Re: 波動関数の連続性
snow さんのレス (2008/10/07(Tue) 06:43)
なるほど,確率の流れ密度が連続だから,波動関数が連続か・・・.
確率の流れに不連続点があると, 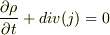 が成り立たないからってことですか?
が成り立たないからってことですか?
Re: 波動関数の連続性
snow さんのレス (2008/10/07(Tue) 06:54)
続けてすみません.
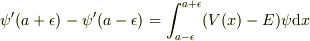 で
で 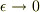 とするときに右辺が0になるのは分かりますが,
これは
とするときに右辺が0になるのは分かりますが,
これは 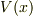 が連続の時も成り立つと思うのですが・・・.
が連続の時も成り立つと思うのですが・・・.
Re: 波動関数の連続性
yama さんのレス (2008/10/07(Tue) 08:59)
>確率の流れに不連続点があると, 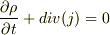 が成り立たないからってことですか?
が成り立たないからってことですか?
そういうことです.
>これは 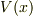 が連続の時も成り立つと思うのですが・・・.
が連続の時も成り立つと思うのですが・・・.
もちろんそのときも成り立つと思います.
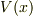 と
と 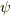 が有界でさえあれば,この式から
が有界でさえあれば,この式から 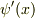 が連続であることが導かれるので,その場合は当然
が連続であることが導かれるので,その場合は当然 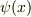 も連続になります.
しかし,
も連続になります.
しかし, 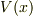 が無限大になる場合は,これは成り立たないので,
が無限大になる場合は,これは成り立たないので, 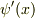 が不連続になることもあります.
が不連続になることもあります.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/07(Tue) 13:47)
> 確率の流れの密度が連続でなければならないのは,そうでないと確率の流れの密度の不連続点(3次元の場合は不連続面)で確率の流れに湧き出しや吸い込みがあることになるからです.
これはちょっと納得できません.  や
や 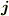 が発散する点があると確率解釈に支障が出そうだというのは理解できますが,
が発散する点があると確率解釈に支障が出そうだというのは理解できますが, 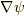 が有界でないことから即
が有界でないことから即
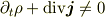
につながるとは思えないのですが.
Re: 波動関数の連続性
yama さんのレス (2008/10/07(Tue) 16:18)
粒子数の保存を前提としているシュレーデインガー方程式では,確率の保存が成り立つことになりますが,そのためには連続方程式が成り立つ必要があります.
その場合, 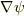 が有界でなければ,
が有界でなければ, 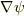 の特異点で流れの密度が発散することになり,連続方程式が意味を持たなくなると思います.
の特異点で流れの密度が発散することになり,連続方程式が意味を持たなくなると思います.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/07(Tue) 17:40)
> 連続方程式が意味を持たなくなると思います.
流れの密度が有限でなければいけないことが 「連続方程式が意味を持たなくなる」からだというのはまだ納得できません.
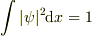 が破れることに直接つながるようには思えないので.
が破れることに直接つながるようには思えないので.
Re: 波動関数の連続性
yama さんのレス (2008/10/07(Tue) 21:30)
確かに, 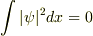 が破れることに直接はつながりません.
が破れることに直接はつながりません.
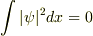 は空間全体の確率の保存を意味するので,それが成り立たねばならないのは当然です.
しかしそれだけでなく,確率の保存は局所的にも成り立たねばならず,それが連続方程式で表されるのだと思います.
は空間全体の確率の保存を意味するので,それが成り立たねばならないのは当然です.
しかしそれだけでなく,確率の保存は局所的にも成り立たねばならず,それが連続方程式で表されるのだと思います.
Re: 波動関数の連続性
mNeji さんのレス (2008/10/07(Tue) 22:49)
横から失礼します.
snowさんの「2008/10/07(Tue) 06:43 No.21728」に関連してコメント申し上げます.
>確率の流れに不連続点があると, 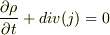 が成り立たないからってことですか?
が成り立たないからってことですか?
この場合,それぞれの項目を明示的に書く下さないと,論議が噛み合ないと思います.ただ,自分には一貫した説明が出来ないのが残念ですが....
例えば,確立密度に関しては, 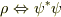 と対応付け出来る様な気がしますが,流れ
と対応付け出来る様な気がしますが,流れ 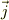 をどう定義して行くのでしょうか.
をどう定義して行くのでしょうか.
Re: 波動関数の連続性
snow さんのレス (2008/10/08(Wed) 00:50)
mNejiさん,すみません. 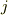 の定義などを書くべきでしたね.
上のyamaさんの定義通りです.
の定義などを書くべきでしたね.
上のyamaさんの定義通りです.
Re: 波動関数の連続性
mNeji さんのレス (2008/10/08(Wed) 05:17)
惚けた質問をして申し訳有りません.量子力学は苦手で,本も持っていませんので.
そうすると,snowさんのご質問の意図が判らなくなるのですが....
厚かましいお願いかも知れませんが,その流れを基に,どのような事が導きだせるがをご論議いただけると幸いです.
Re: 波動関数の連続性
なんとなく さんのレス (2008/10/08(Wed) 11:11)
ちょっだけ参加させてください. yamaさん,Hiroさんの議論はそのとおりですが,もっと易しい(?)説明が必要な気がします.私自身は,学生時代,φ(x),φ'(x)の有界,連続性は,これを”物理的要請”として置く,と言う風に教わりました.その上で勿論確率解釈に必要な規格化,確率密度の連続性が定義される,という順序だったように思います.まあ,量子力学の理念,定式化は一通りではなく,同等な結論を導くやり方が複数あることは事実ですから,どれかが唯一正しいものと言うものでもない気がします. ただ,例えば矩形のポテンシャルは同一座標上に複数の値をもつなど,現実の観測と相容れない(こととして)極限で定義せざるを得ない,極論すれば物理的ではない状況です.そのようなケースに上記波動関数の要請をも適用するかどうかは,yamaさんが言われた有界でない場合のケースバイケースではないのでしょうか.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/08(Wed) 14:06)
「波動関数は連続でなければいけない」という物理的要請はいったいどこからくるのか?
これは確率解釈からの要請だろうという点では,わたしとyamaさんの論点は一致しています.
ただ違うのは,波動関数は連続でないことで,密度やカレントが発散すると, 「(局所)確率保存則が破綻するからだめである」がyamaさんの意見であり, 「大域的な確率解釈が破綻する(だろう)からダメである.」が私の意見ということです.
二人の違いを要約すると,破綻するのが,局所的な確率保存 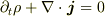 か,大域的な確率の保存
か,大域的な確率の保存 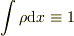 か,の違いではないかと思います.
か,の違いではないかと思います.
Re: 波動関数の連続性
MXK さんのレス (2008/10/08(Wed) 15:44)
ちょっとはずしているかも知れませんが,
連立1階方程式
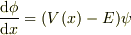
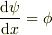 だと思うと,今の場合,話が簡単になるのではないでしょうか.
だと思うと,今の場合,話が簡単になるのではないでしょうか.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/08(Wed) 18:48)
定常な問題に話を限れば,確率解釈からの要請は
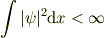
だけで十分のような気がします.
つまり,波動関数は2乗可積分(プラス,有界)であれば不連続でもよいのではないかな.
Re: 波動関数の連続性
yama さんのレス (2008/10/08(Wed) 21:08)
局所的な確率保存を意味する連続方程式は,シュレーディンガー方程式から導かれます. 従って,局所的確率保存はシュレーディンガー方程式に外部から付け加えられる条件ではなく,シュレーディンガー方程式自体の中に含まれているものです.
シュレーディンガー方程式 → 連続方程式(局所的確率保存)→ 波動関数の連続性
ということです.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/09(Thu) 15:02)
> シュレーディンガー方程式 → 連続方程式(局所的確率保存)→ 波動関数の連続性
ということは「波動関数の連続性」はシュレーディンガー方程式以前に,a prioriに,要請することでなく,シュレーディンガー方程式から導かれるということでしょうか?
Re: 波動関数の連続性
yama さんのレス (2008/10/09(Thu) 15:51)
そういうことになりますね.
Re: 波動関数の連続性
なんとなく さんのレス (2008/10/09(Thu) 17:11)
Hiroさん: >aprioriに,要請することでなく,シュレーディンガー方程式から導かれるということでしょうか? yamaさん: >そういうことになりますね.
正直いえば,自信は無いのですが,直観的に(といっても私の直観はそう当てにはなりませんが)理解不能です. たとえば,シュレディンガー方程式から確率の流れを計算するとき,部分積分によって,無限遠の寄与を落とします(有界性の仮定)が,その被積分関数であるφ,φ'の連続性は暗黙に仮定されています.確率の流れが計算出来ないから波動関数が連続でなければならない,というのは主客転倒な気がします.もし,そうなら,有界性もまた同じで,シュレディンガー方程式からの要請であることにならないでしょうか.確かにシュレディンガー方程式を量子力学の基礎方程式と認めてしまえば,そのような言い方もできるかもしれませんが,局所場の理論としての波動関数の実在性に関わる性質を論議するには,経験的(ア・プリオリ)な側面を廃除するものではない気がします.蛇足ですが,物理的要請とは,経験上知られている物理量(勿論存在も含めて)の観測事実と矛盾しない,と言う意味です.
Re: 波動関数の連続性
yama さんのレス (2008/10/09(Thu) 18:03)
>シュレディンガー方程式から確率の流れを計算するとき,部分積分によって,無限遠の寄与を落とします
局所的な確率の流れを考える場合は,その必要はないと思います.局所的な確率の保存は,任意の有限領域についての考察から導くことができます.
ところで,無限遠での波動関数のふるまいは,シュレーディンガー方程式だけでは決まらず,境界条件などを設定することによって決まります. 多くの場合,無限遠で0になるとしますが,一定の運動量をもつ粒子の場合はそのようにはできません. いずれにしても,境界条件は考えている物理的状況に応じて,方程式とは別に与えられるものであって,ある程度の任意性があります. しかし,ポテンシャルの不連続点でのふるまいは,方程式自体によって決まるものであって,境界条件として与える必要はありません. 実際に方程式を解く場合は,あたかも境界条件のように連続性の条件を課すわけですが,その連続性の条件は,もともと方程式自体に含まれているものであって,方程式と独立に設定できるものではありません. つまり,ポテンシャルの不連続点での条件は,波動関数が連続であるようにしか設定できないわけで,設定の任意性はありません.もしポテンシャルの不連続点で波動関数が不連続になるような条件を設定すれば,そこではシュレーディンガー方程式自体が成.り立たなくなります.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/09(Thu) 21:13)
考えている方程式
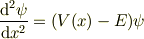
は, 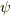 および
および 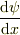 が二乗可積分として,
が二乗可積分として,
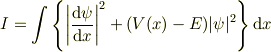
の変分問題と捉え直す事ができます.
# そもそも不連続とか考える場合は弱解の意味で,つまり微分方程式でなく変分問題として考えなければいけませんよね.
どのような 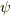 のグループの中で探索するかというと二乗可積分という制限しか必要ないように思います.しかし,
のグループの中で探索するかというと二乗可積分という制限しか必要ないように思います.しかし, 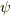 だけでなく
だけでなく 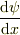 が二乗可積分というのは結構きつい条件なので,波動関数の連続性はこれで決まるのかもしれません.
が二乗可積分というのは結構きつい条件なので,波動関数の連続性はこれで決まるのかもしれません.
# 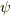 の二乗可積分というより
の二乗可積分というより 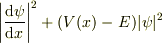 の積分が収束することが条件でしょうが,考え出すとわからなくなるので,とりあえず逃げます.
の積分が収束することが条件でしょうが,考え出すとわからなくなるので,とりあえず逃げます.
Re: 波動関数の連続性
なんとなく さんのレス (2008/10/10(Fri) 10:21)
少し混乱していますが,後学のためにも,不明なことや今の時点で考えていることを書いてみます. Hiroさんの書かれた変分法(原理)への帰着は極めて示唆的だと思います.(古典のみならず)力学の指導原理である,作用積分の変分原理はシュレディンガー方程式も場の方程式も,その出発点ですから理に適っています.そこではヒルベルト空間上のベクトル(波動関数)として2乗可積分は当然として,導関数にまで必要な理由は何でしょう.私にも分かりません.それはともかく,シュレディンガー方程式もその解空間として,この作用と同じ空間と見なせると思います.トートロジーのような気もしますが,そのような空間を選択したこと自体が物理的要請だと思うわけです. yamaさんがいみじくも指摘されたように,自由粒子の波動関数は厳密な意味ではヒルベルト空間の元ではありませんが,波動関数とみなせるのは,シュレディンガー方程式がヒルベルト空間の制限を外せば,他にも解を持ちうることを示唆します. 単純に言えば,2階微分方程式であるシュレディンガー方程式は当然2階(偏)微分が可能であると言えます.そうすると,一階(偏)微分はもちろん可能で連続,且つ滑らか.そして波動関数は連続且つ滑らか,と考えれば,方程式に内包されていると言えると思いますが,それらは区分的でよく,領域を挟んで全空間での連続性と導関数の連続性には直接理由と成らない気がします. つまり,連続性が方程式に内包されている,というのは,純粋に数学的要請ではなくて,解空間を物理的意味づけの出来る(言い替えれば要請される)ものに限るからではないのでしょうか. 境界条件は仰るとおり,方程式(そのもの)とは別の設定であり,波動関数の一般論とは切り離して考えるべき事なのは理解しています.しかし,束縛状態のφ(→∞)〜0というのは”個別の”ポテンシャルケースではなく,”一般的に”自明”とされる,物理的要請と言えるので無いでしょうか. まとめると,対応原理によりシュレディンガー方程式が得られた際,解が物理的に意味を持つものを波動関数として採用する,という条件を置く必要があったのではないかということです.
Re: 波動関数の連続性
yama さんのレス (2008/10/10(Fri) 22:12)
確かにシュレエーディンガー方程式の解がすべて現実の物理状況に対応しているとは言えないでしょう. 何も条件をつけなければ,無限遠で発散する解もありえますが,普通はそのような解は現実にはありえないものとして排除されます.それは物理的要請によるといえるでしょう. 問題はポテンショルの不連続点における波動関数の連続性が,方程式に含まれない物理的要請によるかどうかです. シュレーディンガー方程式は2階微分方程式なので当然2階微分係数が存在しないといけませんが,それが全空間で連続である必要はなく区分的に連続であればよいと思います. 簡単のためポテンシャルが無限大にはならず,階段関数のような不連続性を持つ場合について考えます.波動関数の有界性を仮定すれば波動関数の2階導関数も階段関数のような不連続性を持つことがシュレーディンガー方程式から導けます. ところが階段関数を積分すれば連続関数になるので,1階導関数は全区間で連続になります. つまり物理的要請によらず,数学的に波動関数の導関数の連続性が導かれるわけです.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/10(Fri) 23:09)
> 波動関数の有界性を仮定すれば
結局,ふり出しに戻っている気が....
ポテンシャルが有界なら波動関数は有界であるみたいな論理はできないですかね. あるいは,確率密度の有界性の要請?
Re: 波動関数の連続性
yama さんのレス (2008/10/11(Sat) 00:06)
実際の場面で波動関数の連続性が問題になるのは,不連続なポテンシャルの下での波動関数を求める場合でしょう. この場合はまず不連続点の両側でそれぞれ積分定数を含む一般解を求めます. その一般解が有界であれば,連続条件が成り立つことになるので,それによって積分定数を定めることができます. つまり,波動関数が有界かどうかは一般解を求めてみれば分かることであり,有界であれば安心して連続条件を適用できるというわけです. もし有界でなければ,もちろん連続条件は適用できませんが,少なくとも階段関数型のポテンシャルの場合には,有界でない一般解が得られることはないように思います.
Re: 波動関数の連続性
なんとなく さんのレス (2008/10/11(Sat) 12:54)
Hiroさんの御指摘により,勉強不足だと分かりました. yamaさあ,Hiroさん,割り込みにもかかわらず,有り難うございました.元のスレ主の方もある程度は(何が問題か)形が見えて来たのでは無いかと思います. 後学に勤しむことにして,一端,筆を置きます.
Re: 波動関数の連続性
snow さんのレス (2008/10/11(Sat) 14:51)
すみません.Hiroの説明の >不連続とか考える場合は弱解の意味で,つまり微分方程式でなく変分問題として考えなければいけませんよね. の部分がよく理解できませんでした. 弱解という単語の意味がわかりません. 弱解だと変分問題として考える理由も教えてもらえるとうれしいです.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/11(Sat) 18:55)
> 弱解という単語の意味がわかりません.
簡単に言うと,偏微分方程式に任意の関数をかけて積分した積分方程式の解が「弱解」です.部分積分などを行うことにより微分階数を落とすことで制限が弱くなるので,元の偏微分方程式では許されない不連続な解などを含むことができます.
詳しくは偏微分方程式,あるいは,汎関数を扱った本をみてください.
Re: 波動関数の連続性
toorisugari no Hiro さんのレス (2008/10/11(Sat) 19:34)
> ポテンシャルが有界なら波動関数は有界であるみたいな論理はできないですかね.
> 少なくとも階段関数型のポテンシャルの場合には,有界でない一般解が得られることはないように思います.
確かにそうですね.元の質問に対してはこれで完了じゃないでしょうか.
Re: 波動関数の連続性
snow さんのレス (2008/10/12(Sun) 00:23)
皆さん,ありがとうございました. すっきりしました. 本当に感謝しています.これからも分からないことがあったら質問するので そのときはどうかよろしくお願いします.