とっちー さんの書込 (2008/09/27(Sat) 18:27)

ロジスティック方程式の積分なんですけど， dx/dt = r*x*(1-x) これを両辺[x0, x]の積分区間で積分します． ln|x/(1-x)| = ln|x0/(1-x0)| = rt ここで，x!=1,0, x0!=1,0という条件を使ってます．

この式から，解の x(t) = x0/(x0 - (1-x0)*exp(-rt)) を求めたいのですが，どこで絶対値記号を外していいかわかりません．

絶対値記号を適当に外せば，解は求められるのですが， そのタイミングがわからないので，正式な解法がわかりません．

どなたか，ヒントをいただけないでしょうか？

mNeji さんのレス (2008/09/27(Sat) 20:23)

ロジスティック方程式というのは知らないのですが，微分方程式として見れば，変数分離形になりますね；

dx/x - dx/(x-1) = rdt

初期条件，x(t=0)=x0の元で積分できます．「左辺の分数の分母」がゼロを含まない点には留意するべきでしょう．

簡単の為に「r>0」とすれば，積分定数cとして， ln[x(t)] - ln[x(t)-1] =rt +c

ここで，左辺の第一項より，x(t)>0,左辺の第二項より，x(t)>1だから，左辺全体で， x(t)>1．

初期条件より， ln[x0] - ln[x0-1] =r*0 +c

整理して， Ln[{(x/(x-1)} / {(x0/(x0-1)}]=rt

辺々の指数関数をとれば，

{(x/(x-1)} / {(x0/(x0-1)} = e^(rt)

此れをxについて解けば...． 以下略．

とっちー さんのレス (2008/09/28(Sun) 16:58)

返信がりがとうございます． しかし，積分をする所はわかるのですが， 積分をして求められる式から， ln|x/(1-x)| = ln|x0/(1-x0)| = rt

xの解である x(t) = x0/(x0 - (1-x0)*exp(-rt))

を求める時の絶対値記号を外すタイミングがわかりません．

質問がちょっとわかり難かったと思います．すいません．

mNeji さんのレス (2008/09/28(Sun) 17:22)

＞しかし，積分をする所はわかるのですが， ＞積分をして求められる式から， ＞ln|x/(1-x)| = ln|x0/(1-x0)| = rt

この2つの等号が同時に成り立つというのはどういう事でしょうかね．

＞を求める時の絶対値記号を外すタイミングがわかりません．

対数関数の独立変数，ln(z)のz，は正ですよね．z=x/(x-1)として，xに付いて場合分けをするのは駄目でしょうかね．

yama さんのレス (2008/09/28(Sun) 23:08)

横から失礼します．

mNejiさんが指摘されているように ln|x/(1-x)| = ln|x0/(1-x0)| = rt はおかしいですね．

初期条件はあとで考慮することにして，まず一般解について考えます． 一般解は c を任意定数として ln|x/(1-x)|=rt+c すなわち |x/(1-x)|=exp(rt+c) となります．右辺は負にはならないので辻褄は合っています． ここで絶対値をはずすと x/(1-x)=±exp(rt+c) となり，C=±exp(c) と置くと，C は0でない任意の実数となり x/(1-x)=C*exp(rt) となります． なお，C=0 のときは x=0 となり，これも解になるので，C は任意の実数としてよいことが分かります．

初期条件を適用すると，C=x0/(1-x0) となるので，これを一般解に代入して x について解けば，所望の解が得られます．

結局，絶対値がつくことによって C の負の値も可能になるということです．

toorisugari no Hiro さんのレス (2008/09/29(Mon) 11:15)

分数の積分において絶対値は不要です．

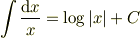
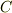( は不定の実数) と高校で習ったと思いますが

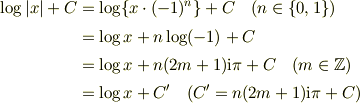
とすれば絶対値ははずれ，その代わり積分定数が複素数になります．つまり，母関数を実数値関数ではなく複素数値関数にまで拡大すれば，対数の絶対値は不要です．

また，問題の

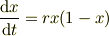
は正接双曲関数をつかって と変数変換する手もあります．

mNeji さんのレス (2008/09/29(Mon) 13:34)

急に思いだして，もう一度，最初の質問を拝見しました．

＞ロジスティック方程式の積分なんですけど， ＞dx/dt = r*x*(1-x) ＞これを両辺[x0, x]の積分区間で積分します．

此処までは覚えていますが，問題は次の部分； ＞ln|x/(1-x)| = ln|x0/(1-x0)| = rt

を読んで，なにを書いてあるのかが判らず，「ロジスティック方程式の積分」を解ければ良いのだろうと言う方向で考えていました．

本来お示しされたかったのは最初の「=」は「-」とした， ln|x/(1-x)| - ln|x0/(1-x0)| = rt ではないでしょうか．

すると， ＞ここで，x!=1,0, x0!=1,0という条件を使ってます．

というのは，初期条件，t＝０の時，x(0)=x0として，解の範囲は； 0 < x(t) <= x(0) < 1 といった条件を示されたかったような気がして来ましたが，どうなんでしょうか．

とっちー さんのレス (2008/09/29(Mon) 18:58)

＞＞ln|x/(1-x)| = ln|x0/(1-x0)| = rt

＞を読んで，なにを書いてあるのかが判らず，「ロジスティック方程式の積分」を解ければ良いのだろうと言う方向で考えていました．

＞本来お示しされたかったのは最初の「=」は「-」とした， ＞ln|x/(1-x)| - ln|x0/(1-x0)| = rt ＞ではないでしょうか．

その通りです． すいません，僕の記述ミスで，みなさんに多大な迷惑をかけたようです．

＞＞ここで，x!=1,0, x0!=1,0という条件を使ってます．

＞というのは，初期条件，t＝０の時，x(0)=x0として，解の範囲は； ＞0 < x(t) <= x(0) < 1 ＞といった条件を示されたかったような気がして来ましたが，どうなんでしょうか．

ただ，こちらはロジスティック方程式を積分する際に， logがゼロにならないように，条件を付けただけです．

ですが，mNejiさん，yamaさん，toorisugari no Hiroさん みなさんのおかげで，疑問に思ってた箇所が解消されました． 本当にありがとうございます．

特にmNejiさんは3回もレスポンスをいただけて，本当に感謝しております． ありがとうございました．