ルンゲクッタ法について
ルンゲクッタ法について
ひで さんの書込 (2008/09/20(Sat) 22:56)
d{f・g}/dt=g+c (cは定数)・・・(1)
という形の式を数値計算により,求めようと思っています.
手法は,オイラー法やルンゲクッタ法を用いるのが一般的だと思うのですが, 左辺がふたつの関数の積になっています.
たぶん,df/dt=f+cの形の式をオイラー法やルンゲクッタ法で解くとすれば, ある時間のfの値をnとした場合,次の時間ステップf_n+1は,(2)式,(3)式で 求めることができると思います.
f_n+1=(f_n+c)・dt・・・・・・・・・・・・・・・・・・・・(2) f_n+1=f_n+dt/6・(k_1(n)+2k_2(n)+2k_3(n)+k_4(n))・・・・・(3)
このやり方で(1)を解くとなると,ルンゲクッタ法を例にとると,以下に式に なりそうですが,正しいですか? 各時間ステップのfとgの値を出すには,なにか,特別な変形が必要でしょうか?
f_n+1・g_n+1=f_n+dt/6・(k_1(n)+2k_2(n)+2k_3(n)+k_4(n))・・・・・(4)
Re: ルンゲクッタ法について
mNeji さんのレス (2008/09/21(Sun) 10:25)
ひでさん,初めまして.
この場合,時刻tから時刻t+dtへ微分増加する時に,関数g(t)は微分方程式(1)によって規定されると思いますが,関数f(t)は関数形が既知の関数として与えられている;
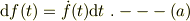
として処理するのでは無いでしょうか.
Re: ルンゲクッタ法について
ひで さんのレス (2008/09/21(Sun) 23:01)
コメント,ありがとうございます.
要は,(4)を用いて,f_n+1・g_n+1の値を求めたら,f_n+1で除して,g_n+1の 値を求めるといった感じでよいのでしょうか?
Re: ルンゲクッタ法について
mNeji さんのレス (2008/09/22(Mon) 00:13)
>要は,(4)を用いて,f_n+1・g_n+1の値を求めたら,f_n+1で除して,g_n+1の 値を求める
では無いと感じます.
基の微分方程式を微分形式にしてみると,
![\mathrm{d}f(t)\cdot g(t) + f(t)\cdot \mathrm{d}g(t) = [g(t)+c]\mathrm{d}t. ---(b)](http://hooktail.maxwell.jp/bbslog/a06a4ea5584950b432813928969701b2.png)
ここで,f(t)は既知関数で,その時間微分が意味を持ち,f(t)もゼロでない有限の値を持つとすれば,g(t) の増分は, 式(a) を用いれば
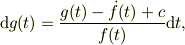
で与えられませんか.右辺は全て数値が確定しますよね.あとは,数値積分の公式で処理できませんか.
なお,次のステップでの関数値は;
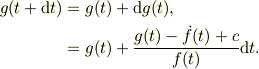
Re: ルンゲクッタ法について
ひで さんのレス (2008/09/22(Mon) 01:13)
すみません.最後のdg(t)の算出で躓いております. 例えば,t=0の初期条件のとき,f(0)=2,g(0)=5と与えられたとしまして, g(1)の値を求める場合などを考えると,f'(0)の値はどう計算すればよい でしょうか? f'(0)=f(1)-f(0)/dtでよいですか?
申し遅れましたが,微分方程式の数値計算法に関しまして,体系的に学んだ 経験がなく,この手の(例えば最初に示した,微分のところが関数の積に なっている)ちょっとひねった類の計算についても,詳しく書かれている 参考書など,もしありましたら,ご紹介いただけますと幸いです. よろしくお願いします.
Re: ルンゲクッタ法について
mNeji さんのレス (2008/09/22(Mon) 01:34)
>f'(0)の値はどう計算すればよいでしょうか? >f'(0)=f(1)-f(0)/dtでよいですか?
f(t)について,何らかの束縛条件なり初期条件は付いていませんか.
例えば,初期条件としてf'(0)が与えられていれば楽ですが.
むしろ, f(t)は本当に未知関数なのでしょうかね.
追伸
私は数値積分を良く知りません.お得意の方からのご助言をお願いいたします.
Re: ルンゲクッタ法について
なんとなく さんのレス (2008/09/22(Mon) 08:52)
こんにちは. 本問への直接レスではないのですが,この微分方程式自体は変数分離法で一般的に解けると思います. f=(1/a)(bexp(at)-1+texp(at)),g=acexp(-at) とおけば(a,bは任意定数),与式を満たします. 結果のチェックに使用できると思います.もう導出済みであれば,無視してください.
Re: ルンゲクッタ法について
toorisugari no Hiro さんのレス (2008/09/22(Mon) 12:32)
ひでさんへ 正確な問題文を完全な形で掲載されることをお勧めします.
すでに何人もの方から指摘されていますが
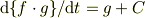
は 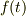 あるいは
あるいは 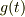 の具体的な関数形か,もう一つの微分方程式がないと,これだけでは解けません.
の具体的な関数形か,もう一つの微分方程式がないと,これだけでは解けません.
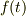 の具体的な関数形が既知なら,
の具体的な関数形が既知なら, 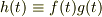 とおいて,以下の
とおいて,以下の 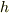 の微分方程式
の微分方程式
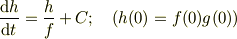
を解いて, 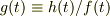 より
より  をもとめられますし,
逆に,
をもとめられますし,
逆に, 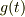 の具体的な関数形が既知なら,
の具体的な関数形が既知なら, 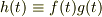 とおいて,以下の
とおいて,以下の 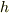 の微分方程式
の微分方程式
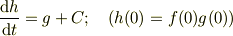
を解いて(これは解析的に解けますね), 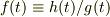 より
より  をもとめられます.
をもとめられます.
Re: ルンゲクッタ法について
ひで さんのレス (2008/09/28(Sun) 23:32)
すみません.問題をそのまま掲載すると,丸投げのような感じがしてためらって おりました.
問題はこうです.
あるダムがある.富栄養化の原因物質が上流の川から流入している.このとき, 流量はQ1(m3/s),流入濃度はcin(mg/L)である.また,ダムからはQ2(m3/s)の 流量で放流されている.Q1,Q2は,時々刻々と変化する.また,ある時刻tの ダム内の水の体積は水位とダム地形図から容易に求めることができるものとする. ダム内では,原因物質の濃度はkC(mg/(m3・s))で増減する. 時刻tにおけるダム内の濃度Cを求めよ.
そうすると以下のように式を立てられると思います.
d(V・C)/dt=Q1・cin-Q2・C+kC・V
最初にお示しした,f(t)とg(t)が体積と濃度に該当します. もしかして,Vが容易に求められるならば,Vを定数のようにして,ある時間tの 濃度が分かったときの,次の時間t+1の濃度は,時間間隔をdtとすると,
C(t+1)={C(t)+Q1(t)・cin(t)-Q2・C(t)+kC(t)・V(t)}・dt/V(t)
でやるのが,ベストですか?
Re: ルンゲクッタ法について
mNeji さんのレス (2008/09/29(Mon) 00:55)
少し見通しが良くなりましたが,依然として不明点が有ります.
ただ,この場合,水の体積の変動と原因物質の量の変動について,独立な微分方程式を作る必要があるように思います.
例えば,水の体積の保存側,
dV/dt = Q1 -Q2 ---(0)
が,原因物質の量の保存(例えば,お書きの式),
d(V・C)/dt=Q1・cin-Q2・C+kC・V---(1)
と同時に成立する必要があると思います.
さらに,観測量の組[Q1(t),Q2(t),cin(t)]から[C(t)]を算出するとか,[Q2(t)]のモデル関数を推定するとか,問題の意図に依存すると思います.
何れにしろ,(1)だけでは無いでしょうかね.
Re: ルンゲクッタ法について
ひで さんのレス (2008/09/29(Mon) 22:04)
>>さらに,観測量の組[Q1(t),Q2(t),cin(t)]から[C(t)]を算出するとか
はい.流入のQ1(t),流出のQ2(t),流入の汚染物質濃度cin(t)を観測し, ダム内の汚染物質濃度C(t)を求めるというものです. もちろん,Q1およびQ2は変化するので,体積も変化します. このような状態で,ダム内のC(t)を算出する問題を考えておりました. Q1とQ2が分かったとなるならば,お示しいただいた(0)式はすでに計算 できますので,以下の式を計算すればよいということですよね?
C(t+1)={C(t)+Q1(t)・cin(t)-Q2・C(t)+kC(t)・V(t)}・dt/V(t)
そして,VはQ1とQ2の差より容易にわかるので,d(V・C)/dtのVは微分 演算子の外にでて,以下の式でよいとするのが,一番,てっとりばやい やり方ですか?
V・(dC/dt)=Q1・cin-Q2・C+kC・V
Re: ルンゲクッタ法について
mNeji さんのレス (2008/09/30(Tue) 00:12)
ダムのように大きな系のばあい,ダム内部での拡散とか撹拌などをどう取るとか,「kC・V」の項は,どのような反応なのか,などと頭が痛くなりそうですね.まあ,最初の第一歩としては,ラフにして見当を付けるには良いかも知れません.
さて,濃度保存の式の左辺に,水量保存の式を適用すると,
d(V・C)/dt = VdC/dt +(dV/dt)C = VdC/dt +C[Q1-Q2]
となるので,VdC/dtの式が出ますよね.またV(t)は,水位のデータから測定値として既知と楽でしょうが,なくても,データを元に式(0)を独立に数値積分すれば良い訳です.
いよいよ,数値積分の練習ですね,頑張って下さい.