ジュード さんの書込 (2008/09/18(Thu) 22:07)

こんにちわ．私は一通り統計力学は勉強したつもりの者ですが，演習問題を解いていないので，いまいち使いこなすことが出来ません． 特に，ガウス分布っぽい関数を見つけた時に，その分散（標準偏差）を求めることが出来ずに困っています．何かこの辺りを書いた参考書や演習書を紹介してくださらないでしょうか？ （この提示版にこんなことを書いてはいけないのかもしれませんがよろしくお願いします）

toorisugari no Hiro さんのレス (2008/09/19(Fri) 16:29)

> ガウス分布っぽい関数を見つけた時に，その分散（標準偏差）を求めることが出来ずに困っています．

おっしゃる意味がわかりません．

任意の分布の分散を求める方法(=定義)がわからないと言うことですか?それともガウス分布の分散を求める方法(=計算)がわからないと言うことですか?

具体的な問題を出してもらった方が早いと思います．

ジュード さんのレス (2008/09/20(Sat) 00:47)

＞おっしゃる意味がわかりません．

すいません．急いで書いたもので，完全に説明不足でした．

求めたいと思った関数は，

ｆ(ω)＝(Γ/2)/{(ω-ω0)^2+(Γ/2)^2}です．

本にこの関数は，横軸をωととったときに，半値幅がΓになるとありました．

母関数φ(x)=ΣPn*x^nで求めるやり方があると統計力学の本で読んだのですが， いまいちやり方がわかりません． 上のｆ（ω）をlnｆ(ω)とし，テーラー展開し，以下のようにガウス分布の形に近似

lnf(ω) = lnf(ω0) + (ω-ω0)｛d(lnf(ω0))/dω｝ + (ω-ω0)/2!｛d^2(lnf(ω0))/(dω)^2}

したのですが，なにかまともな方法とは思えなかったので，皆さんはどのようにして標準偏差を求めているのかをお聞きしたいです．（因みに，テーラー展開した結果は，Γの定数倍にはなりました．）

toorisugari no Hiro さんのレス (2008/09/20(Sat) 19:27)

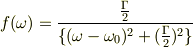
この関数の中心は 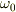，半値幅は確かに 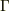ですね． でも分散は発散します． これを分布と観て分散を求めるという意図が理解できません．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/09/21(Sun) 12:08)

確か吸収曲線の形でこの式が出てきました． ローレンツィアンと呼ばれていたと思います．

吸収曲線の形がガウス型かローレンツ型かという議論がされています． 近似という言葉を使うとすると 吸収曲線の形を「ガウスで近似する」か「ローレンツで近似する」かという使い方になります． 圧力を変えるというような条件の変更で吸収曲線の形が変わる時にガウスからローレンツになった（またはその逆）という表現がされます．

ローレンツをガウスで近似するという発想はないはずです． 別々の性質を現す２つの型の１つとして出てきているものです．

こういう吸収曲線の違いにも統計的な裏づけがあると思いますが私には分かりません．とにかく昔のことです．

ジュード さんのレス (2008/09/23(Tue) 12:26)

ｋｏｍａｇａｔａｋｅさん返信ありがとうございます．上に示した式は，誘電体に光を照射した時，電子分極がある時の誘電率の式です．確かにどこかのサイトでこの式をローレンツ型の式と言っていたのを思い出しました．ガウスとローレンツでは，吸収曲線の型自体が違うと言うことなんですか．全く知りませんでした．「統計力学を学ぶ人のために」という本に，「あるｘ0で最大となる山形で，ｘ0を離れると0となるような関数はガウスで近似出来る」と書いてあったのですが，結構荒っぽい近似だったようですね．ありがとうございました．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/09/25(Thu) 11:52)

ジュードさん

＞あるｘ0で最大となる山形で，ｘ0を離れると0となるような関数はガウスで近似出来る

吸収曲線の形を「ある関数」と呼ぶのであればいつでもガウスまたはローレンツで近似出来ます．ピークの部分の丸い所を放物線で近似するか指数関数で近似するかです．ローレンツはガウスに比べてすそが広いです．その分いくらかピークのところがとんがっています．

吸収曲線のすそというのはハッキリしません．バックグラウンドをどう取るかで変わってきます．他の吸収と重なっていても変わってきます．バックグラウンドが変われば半値幅も代わってきます．

お示しの式は複素誘電率から出てきたものだと思いますから幅の部分は誘電損失に当てはまります．分極の遅れを角度表示したものでしょう．

エネルギー損失の原因が他にもあれば幅は変わってきます． ガウスの方は集団の統計的な揺らぎによるものでしょうから原因が異なる事になります．確か磁気共鳴のほうでpressurebroadeningという言葉が出てきたように思います．圧力を加えることで集団の統計的な効果が強く出てきて幅が広がるという現象です．この時にローレンツからガウスに変わるという記述を見たような記憶があります．

ジュード さんのレス (2008/09/26(Fri) 09:28)

ちょうど今，磁気共鳴の辺りを勉強中なので，いろいろと調べてみます．ばかな質問しちゃったかなと自分で思っていましたが，質問当初より頭の中がクリアになってきたので良かったです．ありがとうございました．