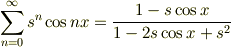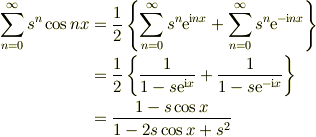フーリエ級数??
Re: フーリエ級数??
mNeji さんのレス (2008/09/15(Mon) 20:23)
証明というよりは,検算みたいな結果になりましたので,お知らせします.
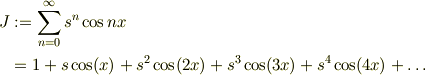
そこで, 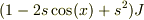 を作り,sの冪で纏めると,
を作り,sの冪で纏めると,
![(1-2s\cos(x)+s^2)J = 1-s\cos(x)+\sum_{n=2}^{\infty} s^n [\cos(nx)-2\cos(x)\cos(nx-x)+\cos(nx-2x)]](http://hooktail.maxwell.jp/bbslog/550d7738eb649c0745e9af7a52bdd7a4.png)
ここで,余弦の和積公式より
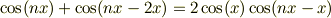
だからs^nの冪の項(n>=2)はすべてゼロとなるので,
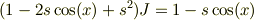
となる様ですね.狐にだまされた様な感じでした.
Re: フーリエ級数??
snow さんのレス (2008/09/16(Tue) 00:10)
ありがとうございます. あのー,これは覚えるべき公式ですか??
Re: フーリエ級数??
mNeji さんのレス (2008/09/16(Tue) 00:37)
>あのー,これは覚えるべき公式ですか??
それが書いてあった所では,どう説明していましたか?
少なくとも,私は始めて見たので計算しただけですから,覚える必要はないと推察します.
Re: フーリエ級数??
snow さんのレス (2008/09/19(Fri) 09:48)
本当だ.すみません,問題文に 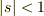 という条件がありました.
お二人さん,ありがとうございます.
という条件がありました.
お二人さん,ありがとうございます.
Re: フーリエ級数??
komagatake さんのレス (2008/09/19(Fri) 11:43)
皆様
ちょっとピンとこない所があります.
|s|<1というのは収束条件だということになりそうです.
でもmNejiさんの式ではnの各項ごとに係数が恒等的に0になっています.これはsの値によらず成り立つということですから不思議な感じがします.
s≧1の場合を考えるといううのは ・無意味なことである, ・その場合でも収束する のどちらなんでしょう.
Re: フーリエ級数??
toorisugari no Hiro さんのレス (2008/09/19(Fri) 13:21)
> s≧1の場合を考えるといううのは > ・無意味なことである, > ・その場合でも収束する > のどちらなんでしょう.
簡単な例で考えましょう.
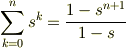
ですから, 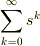 は
は 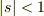 のときのみ収束して
のときのみ収束して
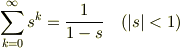
となります.しかし,

のように, 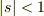 に関係なく,
に関係なく,
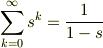
が成立しているようにも見えます.
何か見落としているでしょうか?それとも正しい論理でしょうか? 良い問題なのでみなさんと考えましょう.
Re: フーリエ級数??
yama さんのレス (2008/09/19(Fri) 14:33)
有限級数 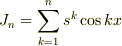 を考えると
を考えると
![(1-s\cos x+s^2)J_n=1-s\cos x+\sum_{k=2}^{n+2}s^k[\cos kx+2\cos x\cos(kx-x)+\cos(kx-2x)]](http://hooktail.maxwell.jp/bbslog/dae85008203d7713b4408ab07f06dced.png)
は成り立たず,余分な項を付け加える(または差し引く)必要があります.
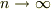 とするとき,|s|<1 ならば,その余分な項が0に収束するのでmNejiさんの式が成り立ちます.
しかし,|s|≧1 ならば余分な項が発散するのでmNejiさんの式は成り立ちません.
とするとき,|s|<1 ならば,その余分な項が0に収束するのでmNejiさんの式が成り立ちます.
しかし,|s|≧1 ならば余分な項が発散するのでmNejiさんの式は成り立ちません.
toorisugari no Hiroさんの場合
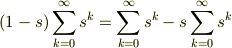
は級数が収束しないときは意味がないと思います.
Re: フーリエ級数??
toorisugari no Hiro さんのレス (2008/09/19(Fri) 14:59)
あああ,もちょっとみんなで悩んで欲しかったんだけど...
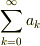 は
は 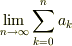 とも
とも 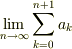 とも,いろいろとれる.
だから
とも,いろいろとれる.
だから 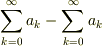 が
が  という言明は
という言明は 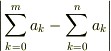 が
が 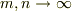 で
で  になるのでないかぎり,つまり,
になるのでないかぎり,つまり, 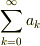 が収束しない限り,無意味ということです.
が収束しない限り,無意味ということです.
# (5)じゃなくて(1)から間違いって指摘するところがさすがyamaさん
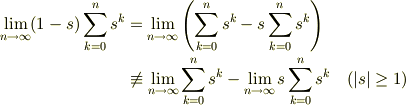
Re: フーリエ級数??
komagatake さんのレス (2008/09/19(Fri) 21:54)
yamaさん toorisugarinoHiroさん
ありがとうございます.
遠い昔に勉強した記憶はあります. 使いこなせる状況にはなっていないというのがよく分かりました.
又よろしくお願いします.
mNejiさんの方法もyamaさんが書かれているような収束条件の吟味を入れてあれば完璧だったということになりますね. 結構スマートな方法だと思います. いきなり無限大で考えるのではなくて,有限のnから→∞で考えるというのがいつの場合でもポイントになりそうだという感じがしました.
Re: フーリエ級数??
mNeji さんのレス (2008/09/19(Fri) 22:50)
>mNejiさんの方法もyamaさんが書かれているような収束条件の吟味を入れてあれば完璧だったということになりますね. >結構スマートな方法だと思います.
数学が嫌いなので,若い時は公式集を手放せなかったものです,言い換えれば,数学は使わせてもらうだけのものと考えていました.でも,この掲示版を観ていると,公式といえども,自分で手を出してみようと言う気になりだしました.その一環で,少し計算を下だけなので,証明した気分になれませんでした.
他方,toorisugarinoHiroさんの解答は,発見的な意味での証明としては素晴らしいと感じました.
勿論,収束性の論議を出来る様な頭が合ったら凄いだろうなと思うこの頃です(笑).