波の表し方
波の表し方
ひよこ さんの書込 (2008/09/12(Fri) 20:52)
一辺が 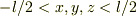 で囲まれる立方体(三次元)の中で,ポテンシャルが
で囲まれる立方体(三次元)の中で,ポテンシャルが 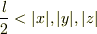 のとき
のとき 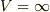 だとすると,シュレディンガー方程式の解として,複素数(
だとすると,シュレディンガー方程式の解として,複素数( 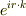 の形)を選ぶのは不適なのでしょうか?
周期的条件
の形)を選ぶのは不適なのでしょうか?
周期的条件 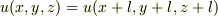 の下での解ならば複素数を選ぶのが都合がいいと教科書に書いてあるのですが,複素数を使用するのは単純に計算が簡単になるからなのでしょうか?
計算の簡略化ならば最初の問題でも複素数形の解を求められるのでしょうか?
電磁波などで複素数を使う理由がまだうまく理解できてません.どなたか教えていただけませんか?
の下での解ならば複素数を選ぶのが都合がいいと教科書に書いてあるのですが,複素数を使用するのは単純に計算が簡単になるからなのでしょうか?
計算の簡略化ならば最初の問題でも複素数形の解を求められるのでしょうか?
電磁波などで複素数を使う理由がまだうまく理解できてません.どなたか教えていただけませんか?
Re: 波の表し方
toorisugari no Hiro さんのレス (2008/09/13(Sat) 11:45)
少し混乱されているようですね.
質問は (1) 無限に深い立方体の井戸型ポテンシャルにおいてシュレディンガー方程式の解として,複素数を選ぶのは何故不適切なのか?
- 一般に偏微分方程式を解くのに何故複素数を使うのか?
の二つですね.
(1)は後回しにして,(2)を答えます. 境界が無視できる(無限に広いor周期境界条件)場合,偏微分方程式を解くのに複素数を使うのは,解法が簡単になるからです.
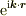 は微分演算子の固有関数
は微分演算子の固有関数
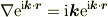
になるので,偏微分方程式,たとえば,
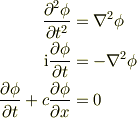
にモード展開
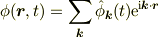
を代入すれば,(対角化された)常微分方程式系
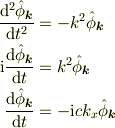
になってしまい,簡単に解けるからです.
Re: 波の表し方
ひよこ さんのレス (2008/09/13(Sat) 23:39)
返信ありがとうございます.お時間とらせてすいません.
> 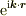 は微分演算子の固有ベクトル
は微分演算子の固有ベクトル
のところは
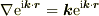 ということでしょうか?
申し訳ないのですが
数学については初心者レベルですので,モード展開についてあまりよくわかりません.
編微分方程式の解が一般的に,級数和で表されることは昔やったことがあるので,モード展開もそのプロセスで解釈してよろしいのですか?
ということでしょうか?
申し訳ないのですが
数学については初心者レベルですので,モード展開についてあまりよくわかりません.
編微分方程式の解が一般的に,級数和で表されることは昔やったことがあるので,モード展開もそのプロセスで解釈してよろしいのですか?
結論についてですが,複素数を使うというのはやはり計算が簡単になるからであって,波(一般の編微分方程式の解として波を選ぶのは適切ですか?)の性質は,オイラーの公式により線形性が保たれているので,解析をする上で物理的意味が崩れないので,一般的に複素数を使ったほうが良いということでしょうか?
Re: 波の表し方
mNeji さんのレス (2008/09/14(Sun) 08:44)
ひよこさん,初めまして.横から失礼します.
量子力学は苦手なのですが,ちょっとコメントします.
[1] 無限大ポテンシャルについて
古典的イメージでは,「運動エネルギ+ポテンシャル・エネルギ=全エネルギ」です.立方体の内部では,各エネルギが有限値で在り得ると思われます.粒子は立方体の壁まで来ると,ポテンシャル障壁に跳ね返されるだけですよね.
量子力学とて「ポテンシャル障壁に跳ね返される」のは同じでも,その表現が違うのだと考えられないでしょうか? もしもその考え方が納得出来なければ,立方体の外側のポテンシャルを, 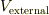 と置いて計算し,その後に
と置いて計算し,その後に 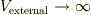 とすれば,解り易いかもしれませんね.
とすれば,解り易いかもしれませんね.
[2] 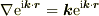
これは, 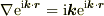 の事ですよね.
の事ですよね.
数学的な詳しい論議は置いといたとして,今必要なのは,定常状態のシュレディンガー(波動)方程式での表現と解の関係が大切だとおもいます.
Re: 波の表し方
yama さんのレス (2008/09/14(Sun) 17:08)
私も横から失礼します.
量子力学の波動関数の場合と電磁波の場合は事情が違うと思います.波動関数は一般には複素数ですが,電磁波は実数で表されます.
従って電磁波の場合は複素数を用いないで方程式を解くこともでき,その場合は三角関数が用いられます.しかし,最終的に実数の解が得られればいいので,途中の計算には複素数を用いてもよく,そのほうが計算が簡単になることが多いようです.
たとえば三角関数の場合, 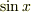 を微分すれば
を微分すれば 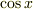 になりますが,複素数の指数関数では,
になりますが,複素数の指数関数では, 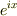 を微分しても
を微分しても 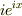 となって関数の形が変わりません.
また,
となって関数の形が変わりません.
また, 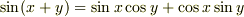 と
と 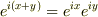 を比べても複素数を用いるほうが見通しがよいと思います.
つまり,電磁波の場合に複素数を用いるのは計算の便宜上のことで,最終的には実数部分をとるなどして実数の解を得るわけです.
これに対して波動関数の場合は,計算の便宜上ではなく,複素数の解になるのが一般的です.しかし境界条件によっては実数になる場合もあります.
を比べても複素数を用いるほうが見通しがよいと思います.
つまり,電磁波の場合に複素数を用いるのは計算の便宜上のことで,最終的には実数部分をとるなどして実数の解を得るわけです.
これに対して波動関数の場合は,計算の便宜上ではなく,複素数の解になるのが一般的です.しかし境界条件によっては実数になる場合もあります.
ご質問の場合について考えてみましょう.この場合のシュレディンガー方程式は,定数を適当に置き換えると 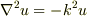 の形になります.
の形になります.
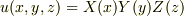 と置いて変数分離すると,次の方程式が得られます.
と置いて変数分離すると,次の方程式が得られます.
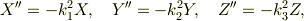
ただし 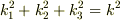 です.
この解として
です.
この解として 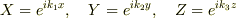 が考えられます.周期的境界条件の場合は,x,y,zのそれぞれの方向の周期に合うように
が考えられます.周期的境界条件の場合は,x,y,zのそれぞれの方向の周期に合うように 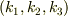 の値を定めることができ,その結果
の値を定めることができ,その結果
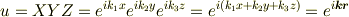
が境界条件を満たす解(の1つ)になります.
しかしポテンシャルの井戸の場合は,この解は境界条件を満たすことはできません.
波動関数は壁のところで0にならねばならないのに, 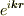 は決して0にならないからです.
この場合,いろいろな
は決して0にならないからです.
この場合,いろいろな 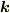 の値について,
の値について, 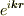 を重ね合わせて境界条件を満たすようにすることも原理的にはできます.しかし,次のように考えるほうが見通しがよいでしょう.
境界条件を満たす解を見つけるために
を重ね合わせて境界条件を満たすようにすることも原理的にはできます.しかし,次のように考えるほうが見通しがよいでしょう.
境界条件を満たす解を見つけるために 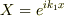 に注目すると,
に注目すると, 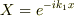 も解であることが分かるので,これらの線形結合
も解であることが分かるので,これらの線形結合 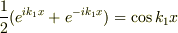 をつくると,これは0になりうるので
をつくると,これは0になりうるので 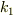 の値を適当に定めれば
の値を適当に定めれば 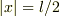 における境界条件を満たすことができます.
における境界条件を満たすことができます. 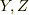 についても同様に考えて境界条件を満たすように
についても同様に考えて境界条件を満たすように 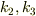 を定めることができます.その結果,立方体の内部では
を定めることができます.その結果,立方体の内部では
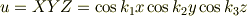
が境界条件を満たす解(の1つ)になります.もちろん,この場合は初めから 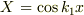 のような実数解を考えることもできるわけです.
のような実数解を考えることもできるわけです.
Re: 波の表し方
ひよこ さんのレス (2008/09/14(Sun) 18:48)
>>mNejiさん 返信ありがとうございます.
>量子力学とて「ポテンシャル障壁に跳ね返される」のは同じでも,その表現が違うのだと考えられないでしょうか?
なるほど,表現の仕方ということですね.少し,数学的に考えすぎたかもしれません.目が覚めました.
>>yamaさん 返信ありがとうございます.
>これに対して波動関数の場合は,計算の便宜上ではなく,複素数の解になるのが一般的です.しかし境界条件によっては実数になる場合もあります.
これは,非常に興味深いと思いました. 複素数を電磁波のときのように使うのは,意味が違うわけですね.初めて知りました.
ポテンシャル井戸の場合でも,解は複素数の線形結合として現れ,結果的に実数になるということですか. いや,また数学的になりすぎました.ようするに古典論と量子論の表現の違いといったところですか.
なんとなく理解できたような気がします.みなさんありがとうございました.
Re: 波の表し方
yama さんのレス (2008/09/14(Sun) 20:57)
電場や磁場は測定できる物理量なので実数で表されます. しかし,波動関数は測定できる物理量ではないので,実数である必要はありません.
Re: 波の表し方
mNeji さんのレス (2008/09/14(Sun) 22:26)
>ポテンシャル井戸の場合でも,解は複素数の線形結合として現れ,結果的に実数になるということですか. >いや,また数学的になりすぎました.ようするに古典論と量子論の表現の違いといったところですか.
何か抵抗を感じます.この場合,ポテンシャル障壁が無限大でないけれど,井戸の内部での運動エネルギよりは十分に大きい場合を考えますと,井戸の外側での運動エネルギ相当の項が負になり,言い換えると波数の自乗が負になるので,本来は波導関数が 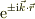 と進行波の重畳で合ったのが,
と進行波の重畳で合ったのが, 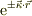 のような単調減少関数になる為だとおもいます.敢えていえば,逆トンネル現象とでも言えるかも知れませんね.
のような単調減少関数になる為だとおもいます.敢えていえば,逆トンネル現象とでも言えるかも知れませんね.
でも,類似現象として,金属に入射した電磁場が金属中に定在波で侵入出来ずに,ジュール熱をだしながら内向きに減衰進行する過程があるとおもいます.電磁場は波動関数と違い,本質的に実関数です.それを除けば,真空中での振る舞いは進行波の重ね合わせで洗わせられているのも,この場合の井戸内部(ポテンシャルV=0)の解が同様に進行波の重ねあわせであるのとも同じです.
すこし極論かも知れませんが,量子力学と電磁気学の違いを確実に認識しておく限りにおいて,むしろ両者の物理的な類似性にも注目したいですね.