ふと思ったのですが

Robio さんの書込 (2008/09/11(Thu) 17:53)

時速100kmで走る電車の中を時速4kmで歩く人がいたとして，その人を外から観察すれば，その人は時速104kmで移動していることになりますよね？

じゃあ，時速100kmで走る台の上に時速100kmで走る台を乗せて，さらにその上に時速100kmで走る台を乗せて…と延々と繰り返して最後にその上に乗れば，その人は高速を超えるんじゃないでしょうか？（汗

光速でいいよね？？

なんか面白そう！！

特殊相対論でよく例に出される問題ですね．結論は光速は超えません．

u[m/s] で動く台Aと，それに対して v[m/s] で動く台Bを考えると，地上からみたBの速度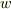は

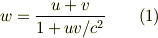
$w=\frac{u+v}{1+uv/c^2} \qquad (1)$

となります（は光の速度）．(1)は変形すれば

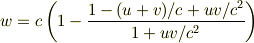
$w=c\left(1-\frac{1-(u+v)/c+uv/c^2}{1+uv/c^2}\right)$

となり，wは光の速度を超えられないことが分かります．

なぜ合成速度は 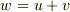w=u+v ではなく(1)になるのかは特殊相対論によるものです．

合成速度はw=u+vにならないのですか… 知らなかったですでは，100km/hの電車内で4km/h歩く人は，厳密にいえば104km/hではなかったってことですかおそるべし特殊相対論！すっきり解けました．ありがとうございましたm（_ _）m