相対性理論
相対性理論
eKinetic さんの書込 (2008/09/07(Sun) 09:07)
高速で走っている電車の屋根に電球を直列に接続して一列にならべて点灯し,スイッチを切る.これを,電車の中にいる人が見ると,すべての電球が一斉に消えるが,地上にいる人が見ると,電球が順番に消えていく.
という話を聞いたことがあります. このとき,地上にいる人が見ると順番に消えていくというのは,電車の先頭から順に消えていくのでしょうか,それとも,電車の後方から消えていくのでしょうか. あるいは,見る場所によって異なるのでしょうか.
どうぞよろしくお願いいたします.
Re: 相対性理論
ミュフ猫 さんのレス (2008/09/07(Sun) 11:54)
結構,ややこしい気がする・・・.
Re: 相対性理論
DIO さんのレス (2008/09/07(Sun) 14:06)
同時性の問題ですね.
電車に固定された座標系において電球の位置を電車の先頭から 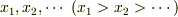 とし,電車の中から見て消えた時刻を
とし,電車の中から見て消えた時刻を  とします.すると,ローレンツ変換より地上の人から見て
とします.すると,ローレンツ変換より地上の人から見て 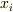 が消える時刻は
が消える時刻は
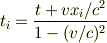
となります.  は電車の速さ,
は電車の速さ,  は光の速さです.今
は光の速さです.今 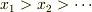 ですので,
ですので, 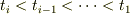 となります.つまり,電車の後方からということですね.
なお電車の速さを決めたら実際どれぐらいの時間差が生じるか計算できます.車両の長さを
となります.つまり,電車の後方からということですね.
なお電車の速さを決めたら実際どれぐらいの時間差が生じるか計算できます.車両の長さを 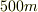 ,速さを
,速さを 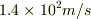 (約時速500km)とすると,電車の最後尾の光が消え,先頭の光が消えるまでの時間は
(約時速500km)とすると,電車の最後尾の光が消え,先頭の光が消えるまでの時間は
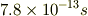
です.(数値計算を間違えているかもしれません,,
Re: 相対性理論
DIO さんのレス (2008/09/07(Sun) 14:28)
続けてすいません.
上の数値計算があっていれば相対論的な効果による時刻の違いより,単に光が伝わる速さが有限であることからの時刻の違いの方が大きいかと思います.
地上での観測者の目の前に一番後ろの電球が来たときに電球を消せば,上の数値で行くと,先頭の電球の光が観測者に届くまでに約 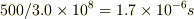 かかります.
かかります.
ですので,実際問題は前から消えるか,後ろから消えるかは見る場所によって異なると思います.
Re: 相対性理論
eKinetic さんのレス (2008/09/07(Sun) 22:56)
ミュフ猫さん,DIOさん,ありがとうございました.
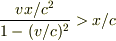
を解いて,
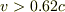 程度であれば,相対論的な効果によって,電車の後方から電球が消えていく,という理解をしました(間違っていたらご指摘ください).
程度であれば,相対論的な効果によって,電車の後方から電球が消えていく,という理解をしました(間違っていたらご指摘ください).
いろいろご教示いただき,ありがとうございました.
Re: 相対性理論
DIO さんのレス (2008/09/07(Sun) 23:45)
eKineticさん,大変失礼しました.No.21516のローレンツ変換の式にルートを付け忘れていました.正しくは
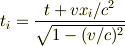
でした.
またNo.21517の所では忘れていたのですが,この速さになると電車の長さの縮小も考えなければならないので,地上の観測者から見た電車の長さ  は
は 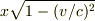 となります.eKineticさんの不等式の右辺の
となります.eKineticさんの不等式の右辺の  をこれに変える必要があります.
ローレンツ変換の式も間違えていたので修正後も修正前と同じ結果が得られてしまいました(笑,,
をこれに変える必要があります.
ローレンツ変換の式も間違えていたので修正後も修正前と同じ結果が得られてしまいました(笑,,
不備ばかりですみません.
Re: 相対性理論
toorisugari no Hiro さんのレス (2008/10/06(Mon) 19:34)
> 高速で走っている電車の屋根に電球を直列に接続して一列にならべて点灯し,スイッチを切る.これを,電車の中にいる人が見ると,すべての電球が一斉に消えるが,
すでにここから変です.
一つのスイッチでON/OFFした場合,直列に接続された電球は同時には点灯しません.スイッチON/OFFの情報はせいぜい光速でしか伝わらないからです.
また,複数の同期した時計を使って,複数の電球を「同時」に点滅させた場合でも,光速が有限であることから,電車の中にいる人にとっても「すべての電球が一斉に消える」様には「見え」ません.
「異なる2点A,Bの事象のどちらが先に発生するか」と「異なる2点A,Bの事象のどちらが先に観測されるか」は違う問題ですから,これを区別しないと無意味な議論になります.