ばねの問題です. 教えてください
ばねの問題です. 教えてください
リリー さんの書込 (2008/09/05(Fri) 03:18)
大学1年のりりーです.ばねの問題ですが,教科書などで調べたのですがいまいち解き方がわかりませんでした.問題は, 質量m,ばね定数kの2つのばね振り子をばね定数k’のばねでつなぐt=0の時,x1=a, x2=0,] ・・ x1=x2=0として,2個のおもりの運動を調べろ.ただし摩擦や空気抵抗は考えなくてよい. 図は壁の両端にばね定数kのばねがある感じです. 壁ーばね(ばね定数k)−おもりm−ばね(ばね定数k’)−おもりm−ばね(k)−壁のようになっています. という問題なんですが,解き方考え方がまったくわかりません. 具体的に教えていただけたらとてもありがたいです.よろしくお願いします.
Re: ばねの問題です. 教えてください
リリー さんのレス (2008/09/06(Sat) 14:36)
DIOさんありがとうございます.左右に揺らすのかわからないんですが,おもりの運動を調べるというのはどのように考えたらわかりやすくなりますか?
Re: ばねの問題です. 教えてください
DIO さんのレス (2008/09/06(Sat) 15:51)
結局,左右に揺らしても上下に揺らしても,運動の様子は同じようになると思うのでどちらでも良いのかも知れません.
問題で問われている,運動を調べよと言うのは 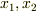 を
を  の関数として求めよという事だと思います.
の関数として求めよという事だと思います.
具体的に 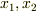 を解いてみると
を解いてみると 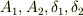 を任意定数として
を任意定数として
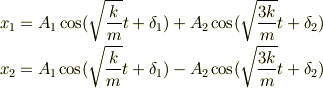
となります.この時 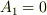 と時と
と時と 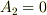 の時は
の時は 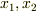 は互いに振動数の等しい単振動をします.この特殊な運動の形をノーマルモードと言い,一般解はノーマルモードの重ね合わせで表されます.
は互いに振動数の等しい単振動をします.この特殊な運動の形をノーマルモードと言い,一般解はノーマルモードの重ね合わせで表されます. 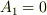 というのは
というのは  で
で 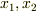 を反対方向に同じだけずらして離したときに生じる運動で,
を反対方向に同じだけずらして離したときに生じる運動で, 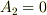 というのは
というのは  で
で 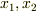 を同方向に同じだけずらして離したときに生じる運動です.これらの運動はイメージしやすいかと思います.
一般的にノーマルモードは自由度の数だけ存在します.この問題は自由度が2すので,ノーマルモードが2つあったわけです.
自由度がもっと多くなったときはこの事を使って解くのが良いかと思います.つまり,運動方程式を立ててやった後に,それぞれの変位が単振動の型だとして特殊界を見つけてやり,その重ね合わせとして一般解を導くのです.
を同方向に同じだけずらして離したときに生じる運動です.これらの運動はイメージしやすいかと思います.
一般的にノーマルモードは自由度の数だけ存在します.この問題は自由度が2すので,ノーマルモードが2つあったわけです.
自由度がもっと多くなったときはこの事を使って解くのが良いかと思います.つまり,運動方程式を立ててやった後に,それぞれの変位が単振動の型だとして特殊界を見つけてやり,その重ね合わせとして一般解を導くのです.
Re: ばねの問題です. 教えてください
リリー さんのレス (2008/09/07(Sun) 22:04)
DIOさん詳しい説明ありがとうございます.参考にさせていただきます. またわからなくなった時はよろしくお願いします.
Re: ばねの問題です. 教えてください
リリー さんのレス (2008/09/08(Mon) 01:52)
DIOさん,たびたび申し訳ないんですが問題に出てくるばね定数k’のばねがありますが答えを求める際には必要ないのですか?
Re: ばねの問題です. 教えてください
DIO さんのレス (2008/09/08(Mon) 09:21)
すみません,完全にダッシュを見逃しておりました. 運動方程式を立て直すと,
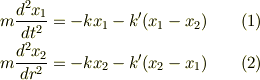
となり,(1)+(2),(1)-(2)より
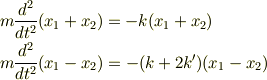
です.
すいませんでした.しかし考え方はそのままです.
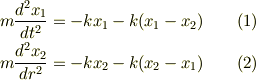
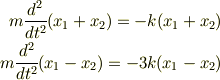
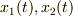 が出ます
が出ます