力学 バネ(単振動)について
力学 バネ(単振動)について
トワイス さんの書込 (2008/09/03(Wed) 22:39)
力学の単振動についての問題で説き方がよく分からないのがあるので,教えてください.
↑y ● ↑y=h y=0−● | > < > | −−−−−−−−−
図のように,質量の無視できるバネ定数kの十分に長いバネが鉛直に立てられており,その上に質量mの物体Aが取り付けられている.重力とバネの復元力がつりあっているときの物体Aの位置をy軸の原点にとる.物体は鉛直方向にのみ動くものとして,以下の問に答えよ.但し,重力加速度をgとする. 物体Aの真上のy=hの位置から同じ質量mの物体Bを初速度0で落下させた. 物体Bは物体Aと完全非弾性衝突をし,物体Aと一体となって運動を続けた. (1)一体となった物体の衝突直後の速さを計算せよ. 一体となった物体は最下点に達した後,上昇を初め,ある位置になったときに,物体Bは物体Aからはなれた.衝突してから離れるまでの運動は単振動である. (2)単振動の中心のy座標と,単振動の角振動数をそれぞれ計算せよ. (3)最下点のy座標を計算せよ. (4)物体Bが物体Aから離れる位置のy座標を計算せよ.
上記の問題で,(1)は,
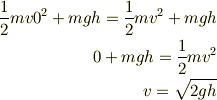
と求めて, (2)は, 物体ABがくっついた状態でバネとつりあいの状態でとまっているところと考えて,
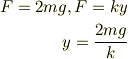
と,ここまで考えられるんですが,(2)の角周波数を求める方法が分かりません. そして,次の(3)を求めるやり方もいまいちよくわかりません. (4)は,(3)と(2)で求めた中心の位置があれば求められそうなのですが…… (1),(2)の考え方があっているかも一応教えてもらえるとありがたいです.
Re: 力学 バネ(単振動)について
DIO さんのレス (2008/09/03(Wed) 23:12)
(1)トワイスさんの解は衝突直前の速さです.ここから運動量保存則より衝突直後を出します.
(2)y軸は上向きが正だと思うのですが,そうであれば答えはマイナスが入ります.
運動方程式を作ると
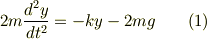
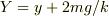 とすると(1)は
とすると(1)は
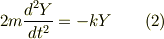
となり,これを解き,そこから必要な値を得ます.
ただ,公式的なものを使ってよいなればここから角振動数はここから出ますし,(3)は別にエネルギーの観点から行けば答えが出せます.最下点では速さが0ですので,
(4)最下点から考えて,加速度が初めて負になる地点ですので,これは(2)で求めた単振動の中心と一致します.
Re: 力学 バネ(単振動)について
mNeji さんのレス (2008/09/04(Thu) 18:53)
横から失礼します.
始めの質問にある,
>物体Bは物体Aと完全非弾性衝突をし,物体Aと一体となって運動を続けた.
という記述と,
>(4)物体Bが物体Aから離れる位置のy座標を計算せよ.
という記述の間には,何らかの仮定というか,条件がないと困る様に思います.
例えば,物体Xに物体Yが完全非弾性衝突をしたら,一体となった物体Zになってしまう訳ですね.どうやって元に戻すのでしょうか?
Re: 力学 バネ(単振動)について
DIO さんのレス (2008/09/04(Thu) 19:39)
>mNejiさん
最下点から,単振動の中心までは物体Aにかかる力は上向きであり,それは物体Bにまで伝わります.しかし,単振動の中心点に達すると,Aにかかる力は下向きになり,それはBには伝わりません.
Re: 力学 バネ(単振動)について
mNeji さんのレス (2008/09/04(Thu) 20:32)
>最下点から,単振動の中心までは物体Aにかかる力は上向きであり,それは物体Bにまで伝わります.しかし,単振動の中心点に達すると,Aにかかる力は下向きになり,それはBには伝わりません.
問題から推察するとそうなんでしょうね.しかし,定義が明確でない様におもわれるので,問題としては明示的にする必要があるように感じました.割り込み質問,失礼しました.
Re: 力学 バネ(単振動)について
トワイス さんのレス (2008/09/05(Fri) 10:21)
DIOさん,ありがとうございます. 一応ヒントを元にといてみたのですが,また質問させてください. (1)の答えは,
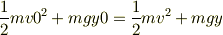
v0=物体Bの初速度=0,y0=物体Bの初期位置=hv=物体A+Bの速度,y=衝突の瞬間の位置=0 よって,
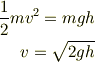
そして,
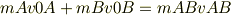
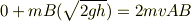
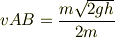
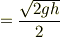
と出しました. (2)は, F=-2mg ,F=-ky F=0の地点なので,
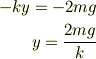
これだと,マイナスが出ないのですが,Fの式が間違っているのでしょうか?
(3)は, 最下点とy=0の地点での力学的エネルギー保存則を使って, 最下点の位置を-Y.速度は0.y=0での速度をv.位置は,0なので,
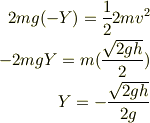
と出しました.あっているでしょうか?
Re: 力学 バネ(単振動)について
DIO さんのレス (2008/09/06(Sat) 10:42)
(1)あっていると思います.
(2)恐らく,重力が下向きで,バネの力が上に向いていることからこの式を立てられたと思うのですが,バネの力 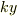 の
の  は絶対値では無いことに注意して下さい.この問題での座標の取り方だとバネの力は
は絶対値では無いことに注意して下さい.この問題での座標の取り方だとバネの力は 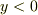 のとき正(上向き),
のとき正(上向き), 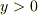 のとき負(下向き)です.ですからつり合いの式は
のとき負(下向き)です.ですからつり合いの式は
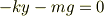
となります.
(3)バネのエネルギーを忘れています.
このような設定の時には,バネと重力のエネルギーを合わせて位置エネルギーと考えて解くのが良いかと思います.
まずNo.21472の(2)の運動式を作ります.このように変形すると,そこには既に 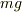 はありませんので重力のエネルギーを別に考える必要が無いのです.すると,
はありませんので重力のエネルギーを別に考える必要が無いのです.すると, 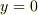 で
で 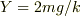 なのでエネルギーの関係は
なのでエネルギーの関係は
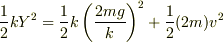 となります.最後の項の
となります.最後の項の  は(1)で求めたものです.これで出た
は(1)で求めたものです.これで出た 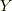 から
から 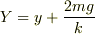 より得る
より得る  が答えです.
が答えです.
単振動の問題で重力などの他の力が関わる場合は
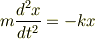
の形に変形してやるのがキーポイントだと思います.
Re: 力学 バネ(単振動)について
トワイス さんのレス (2008/09/08(Mon) 05:37)
DIOさん,再度ありがとうございます.
(3)なのですけど,
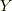 に取るのがなぜ,
に取るのがなぜ, 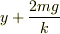 なのでしょうか?
(2)の中心点での答えの
なのでしょうか?
(2)の中心点での答えの 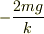 で,
で, 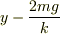 ではないのでしょうか?
そうすると運動方程式が出来ないのはわかるので,+でいいんでしょうが,
+で取る理由が分かりません.
また,上で求めた運動方程式の左辺のmの前にある2は位置エネルギーを求めるときなにか,影響しないのでしょうか?
ではないのでしょうか?
そうすると運動方程式が出来ないのはわかるので,+でいいんでしょうが,
+で取る理由が分かりません.
また,上で求めた運動方程式の左辺のmの前にある2は位置エネルギーを求めるときなにか,影響しないのでしょうか?
上記で質問しましたが,一応+での場合で式を立て,やってみました.
(3)
Yでの運動方程式を求めて,
力学的エネルギー保存則をYでの点(原点)とy=0となる点で求めると,
原点 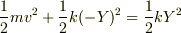 y=0点
y=0点 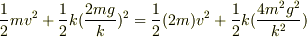 保存則を立てると,
保存則を立てると,
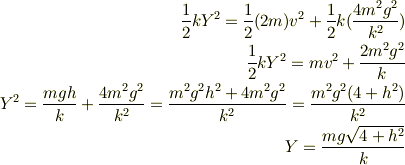
これで,Yを求めたんですが,なぜ, 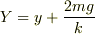 で,Yを代入したときのyが答えなのでしょうか?
で,Yを代入したときのyが答えなのでしょうか?
Re: 力学 バネ(単振動)について
DIO さんのレス (2008/09/08(Mon) 09:29)
となる所が振動の中心です.
とし,右辺のyに(2)で求めた
を入れるとYは0になります.
私の感覚では振動の中心を求めて変数を変えるより,運動方程式をいじって変数を変えてやり中心を見つけるという方がしっくりきます.つまり
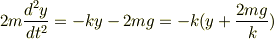
として 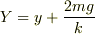 と置いた訳です.ここから
と置いた訳です.ここから 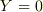 となるのは
となるのは 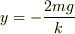 であると分かります.
であると分かります.
>上で求めた運動方程式の左辺のmの前にある2は位置エネルギーを求めるときなにか,影響しないのでしょうか?
この2は 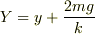 とした
とした 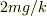 に出てきています.このエネルギーの取り方が正しいことを確認するには,運動方程式の両辺に
に出てきています.このエネルギーの取り方が正しいことを確認するには,運動方程式の両辺に 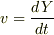 を掛けてやります.
を掛けてやります.
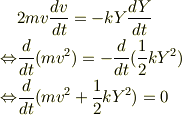
この方法は初めてだと変に思うかもしれませんが,エネルギー保存を考えるためのテクニックのようなものです.
>なぜ, 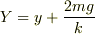 で,Yを代入したときのyが答えなのでしょうか?
y→Yの変数変換は,元あったy軸を平行移動したようなものです.問われているのは元のy座標での値ですので戻してあげなければなりません.また,
で,Yを代入したときのyが答えなのでしょうか?
y→Yの変数変換は,元あったy軸を平行移動したようなものです.問われているのは元のy座標での値ですので戻してあげなければなりません.また, 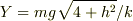 とされていますが,これはマイナスが入ります.
とされていますが,これはマイナスが入ります. 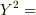 を解くと解は±が付きますが,最下点ですので答えはこのうち負のものです.
を解くと解は±が付きますが,最下点ですので答えはこのうち負のものです.
気になったのですが, 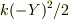 とされているマイナス不要かと思います.ここでは二乗でマイナスが消えていますが,このようにマイナスを入れて失敗していることが上の方で見られました.恐らく,最下点で求める値はマイナスだろうから,と言う理由で付けているものと思われますが,これは不適切です.式を解いてゆけば自然とマイナスが出るか,もしくは上記のように累乗が答えになるでしょう.
とされているマイナス不要かと思います.ここでは二乗でマイナスが消えていますが,このようにマイナスを入れて失敗していることが上の方で見られました.恐らく,最下点で求める値はマイナスだろうから,と言う理由で付けているものと思われますが,これは不適切です.式を解いてゆけば自然とマイナスが出るか,もしくは上記のように累乗が答えになるでしょう.