調和振動子の解の導出
調和振動子の解の導出
トビラ.. さんの書込 (2008/08/29(Fri) 00:44)
みなさんこんにちは,
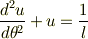
の解が
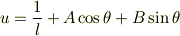
となるそうなのですが,どのように計算すればこうなるのでしょうか.僕は同次二回微分方程式はわかるのですが,これは理解できませんでした. お忙しいとは思いますが,時間があればどうか僕に教えてください.
Re: 調和振動子の解の導出
トビラ.. さんのレス (2008/08/29(Fri) 01:18)
mNejiさんはじめまして. ああ!!確かに・・・ 後は二回微分方程式をつかって計算してその解に
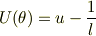
を代入すればいいわけですね. 応用力なくてすみません.(汗) 助かりました.mNejiさんどうもありがとうございました.
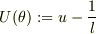 と置くと,どうでしょうか.
と置くと,どうでしょうか.