tai さんの書込 (2008/08/27(Wed) 16:40)

大学1年生で，物理のレポートがわからなかったので， 質問しに来ました．

xy面上を運動する質点のx,y座標が時間tの関数として x=αt^2,y=βt(α,βは定数) と書けるとき，質点の軌道はどのように表されるか．

両方の式からtを消去するのは，わかったのですが， それがどのようなグラフになるのか，また何を表すのか がわかりませんでした．お手数ですが，教えていただけ ないでしょうか．

mNeji さんのレス (2008/08/27(Wed) 16:49)

(x,y)座標から，座標変換して(X,Y)座標になったとします．

この変換が， X=y Y=x だとすると，(X,Y)座標での軌道はどうなるか判りますか？

tai さんのレス (2008/08/27(Wed) 22:49)

返信ありがとうございます．

すいません，わかりません．

tai さんのレス (2008/08/27(Wed) 23:45)

すいません，訂正します． 両方の式からtを消去すると，x=α(y^2/β^2)となるところまで解けたのですが，これをグラフにするには，どのような式にすればいいですか？

mNeji さんのレス (2008/08/28(Thu) 00:13)

＞x=α(y^2/β^2)となるところまで解けたのですが，これをグラフにするには，どのような式

そこで，x→Y，y→X，と書き直して視ると，なにか良く知っている感じになりませんか？

tai さんのレス (2008/08/28(Thu) 08:41)

Y=α(X^2/β^2) 二次関数ですか？

mNeji さんのレス (2008/08/28(Thu) 09:56)

＞Y=α(X^2/β^2) ＞二次関数ですか？

そうですね．ただし，頭を90°回転する必要があります．

で，元に戻りますが，αがゼロでないとすると，xの式をαで割ると，

x/α=y^2/β^2

となります．右辺は自乗項だけなので常に正かゼロです．従って，左辺も常に正かゼロです．そこで，左右両辺のルート(平方根)を取るとどうなりますか？

tai さんのレス (2008/08/28(Thu) 11:36)

√x/α=y/βですか？

mNeji さんのレス (2008/08/28(Thu) 17:38)

左辺は正ですが，右辺のyは正負を取る事に注意すると， ±√x/α=y/β とする方が良いですね．

あとは，見やすく「y=○○」と変形すればどうですか．

tai さんのレス (2008/08/28(Thu) 18:42)

つまりy=±β√x/αですね．

ええと，グラフは，左か右に凸な放物線になるということですか？

mNeji さんのレス (2008/08/28(Thu) 19:00)

＞グラフは，左か右に凸な放物線になる

まさにその通りです．

式ではこのように書くのが解り易いですが，図形とすると，横向きの放物線の方がイメージし易いですね．

tai さんのレス (2008/08/28(Thu) 19:06)

ふと思ったのですが，αとβは定数となっているから，負の場合や0の場合に分けないといけないんですか？

mNeji さんのレス (2008/08/28(Thu) 20:01)

私は，数学的に厳密な論議が得意ではないので上手く説明出来ませんが，不要だと思う条件について，個別的に検討されてみては如何でしょうか．

tai さんのレス (2008/08/28(Thu) 20:33)

わかりました．ありがとうございます． 何度も何度もすいませんが，学校でこの問題を質問したときに， このx/α=y^2/β^2が何を表すのかを答えよといわれたのですが，どうこたえれば いいのですか？

mNeji さんのレス (2008/08/28(Thu) 22:16)

高校の数学の教科書，数研出版の「新編数学C」の第2章式と曲線の第1節2次曲線の1.放物線によると，

A 放物線の方程式

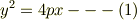
とすると，式(1)を放物線の標準形という．

B y軸が軸となる放物線

次の様になる．

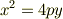
〜〜〜〜〜〜〜〜〜 従って，少なくとも高校の数学の教科書では，単純に「放物線」と言っておけば良い様です．数学は良く判りません．

追記

「放物線逆関数」で検索していたら，次のサイト

・グラフを読む力を付けよう(PDF) www.sit.ac.jp/user/shunsatoh/kiso/sub/hs1.pdf

がありました．ご参考まで．

tai さんのレス (2008/08/28(Thu) 23:44)

mNejiさんなにからなにまでありがとうございます． 参考にします．