ｗｗｗ さんの書込 (2008/08/25(Mon) 16:41)

この問題教えてください． 長さL 密度ρの一様な細い棒ABがある．棒の一端に糸を付けて 密度ρo（ρo>ρ）の水面に浮かべ，糸を張力0からゆっくり力を加えて 引き上げる． 1，点Aが水面から高さhになった時，棒は水面とθの角度 をなしていた．sinθをL,h,ρo,ρで表せ． ２，棒が鉛直になった時のA点の水面からの高さhoを求めよ． お願いします．

mNeji さんのレス (2008/08/25(Mon) 17:54)

この手の問題では，「力のつりあい」と「トルクのつりあい」と連立させて解きますね．このとき，トルクの釣り合いを考える時には，棒の中で，計算し易い所にすれば良い事に注意すれば良いです．

なお，関与する力は３つ； (1)A点での垂直に引っ張った時の張力， (2)棒ABの重心での重力 (3)水没している棒の部分の浮力 に注意して，釣り合いの2式を書いてみたら，如何でしょうか．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/25(Mon) 19:52)

別のサイトに 全く同じ文章の質問が出ています．

何人かの方が回答を書かれていますが質問された方からは何の返事もコメントもない状態でストップしています．

ミュフ猫 さんのレス (2008/08/25(Mon) 20:56)

いや，典型的な「丸投げ網」さんでは？ｗ

mNeji さんのレス (2008/08/26(Tue) 00:09)

「問題の丸投げ」について，私見を述べてみたいと思います．

私は，若い頃，演習問題が大嫌いで，意識して問題を解きませんでした．若気のいたりで，丁寧に勉強すれば問題を解く力は付いている筈なので，一々問題を解くには馬鹿げた事である，と思っていました．その代わりに，自分で問題を考える訓練をしました．

＃今から思えば，効率の悪い馬鹿げた方法論だったと思いますね．

それから何十年も経て，こちらのサイトを拝見するうちに，「具体的に問題を解く」のは「一般的な理解を深める」為に有効だと思う様になりました．

と同時に，「問題の丸投げ」というのは，見方の問題で，一見「問題の丸投げでない」ような質問が，じつは「問題の丸投げ」という逆転現象が頻繁に起こっているように感じています．

とすると，「問題の丸投げ」だからその質問が駄目だ，という論理は破綻しているように思えます．逆に言えば，一度理解出来た人から見れば，「何で判らないのと思える事」が見通せないからこそ質問しているのでしょう．この場合，まずは考え方の概略を説明しても良いのではないかと思うのです．

また，質問者さんが，質問しっぱなしの場合，解答が難しすぎて応答出来ない可能性もあります．実際，自分が流体力学関連で質問した時に，そのような経験があります．

また，同じ問題を他の所でされていても，どうでも良いと思います．この掲示版のように数式表現が明確で，アスキー・アートの環境がある掲示版は他には無い様に思うからです．

ミュフ猫 さんのレス (2008/08/26(Tue) 00:46)

ハ '"´￣￣｀`´/‐ '∠., _ ／ Ｕ,イ ，_ `，

＿_r‐{ -／/,'/ /i ヽ￣｀` :::::ム:::::7/ ∧,/,/l 丶 ::://:::/,' u/Ｘ// ! |／ヽ ;/ !:://l ! / ,/l/`'"，,／!ヽ | l. ', !l//:::|l i. / リi.| ト，.! !l/'''7リ ,l/ ／／／／／／!l, lヽ! | !`l. / /￣￣`iハ. ,! ハ! ｌ`'l/ー ，/ /〉l/,/ ＜そ，そんな発想は出来ん・・・． .! | | `iー--，-',-‐，i" |/

! l ! ／７ヽ，....7M. ハ! i !

. ! !|,!{ /.丶...ヾ,ハK. | | |

ハ ||.| |........ヽ..........i.ヾ ,! | !i.i.||.| |......，...i..../....|.[|,ノ ! ! !| ｌ|}.| |.......ヽ|./........l,..} i |

apple さんのレス (2008/08/26(Tue) 00:52)

自分もmNejiさんの意見に賛成ですね．

でも，少なくとも自分がどこまで分かっているのか，どこから分からなくなったのかぐらいは書くべきではないかと思います．

mNeji さんのレス (2008/08/26(Tue) 01:14)

＞でも，少なくとも自分がどこまで分かっているのか，どこから分からなくなったのかぐらいは書くべきではないかと思います．

う〜む．正論ですね．

今回の問題を拝見したとき，大昔，壁と床に梯子を掛けて，静止する問題に始めて出会った時を思い出しました．力の平衡だけで解けなくて悶々としました．それはそれで良いのかも知れませんが...．

＃正に，理解が不十分な時には，「何が判らないかを判らない」というフェイズがあると思います． ＃だから，「この問題が判らない！」という質問を，私は許容しても良いと思います．

掲示版の機動力というのは，その様な「良く生じる誤解」を容易に訂正して，本質的な理解；この場合は力と偶力の同時成立；を示すことが出来る事だと思うのですが．さらに，「偶力を眺める原点は，都合に合わせて決めうる」という考え方を示すと，剛体系の運動を勉強する為の良い基盤を作れると，感じます．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/26(Tue) 07:32)

ｍＮｅｊｉさんが「掲示板の機動力」という言葉を使っておられます． これは回答に対して質問された方からのレスポンスがあって初めて成り立つものです．質問のしっぱなしではどこに出しても同じ程度の内容の回答しか戻ってきません．回答は質問が引っ張り出すのです． とんでもない誤解をしていてもかまいません．それを見れば「違うよ！」と言うことが出来るのです．

問題集の問題のコピーを貼り付けて「お願いします」という言葉だけで出すのであればどこに出しても同じ回答しか戻ってきません．

別のサイトで貰った回答が難しくて分からなかった，訊いていることと違う方向の回答になっていたというのであればそういう風に言えばいいと思います． でも向こうのサイトでもそういう風に言うべきです．きちんと礼を言って閉めるべきです．（まだ同じ人だと決まったわけではありませんが・・・．）

ｍＮｅｊｉさんの最初の回答に書かれている問１についての考え方の方針と同じ内容のものは向こうのサイトの回答にも書かれています． 誰が書いても最初の回答は同じようなものになります． （問１は高校レベルの問題ですから標準的な回答の仕方は決まっています．問２はちょっと難しいです．）

力の向きが分からない，重心が分からない，浮力が分からない，モーメントが分からない，・・・であればそういう質問を出さないとその説明を引き出すことは出来ません．

向こうのサイトでもこのサイトでも「途中の式はいいから最期の結果だけ教えて欲しい」という質問だとは想定していません．でもそういうことを要求してくる生徒もかなりいます．ｗｗｗさんがそうであるかどうかは分かりませんがこういうサイトに出てくる質問ではその可能性もあります．

mNeji さんのレス (2008/08/26(Tue) 11:20)

ｋｏｍａｇａｔａｋｅさん，

＞これは回答に対して質問された方からのレスポンスがあって初めて成り立つもので す．

私もそう願いたいと思っております．

＞質問のしっぱなしではどこに出しても同じ程度の内容の回答しか戻ってきません．回答は質問が引っ張り出すのです．

これは，面白い観点ですね．息の合った質疑応答の極致ですね．でも，私は質問者さんが必ずしも物理を熱心に勉強されていない場合もあると思います．

自分の高校生の時には，学校の授業は面白くなく，区の図書館で大学の教科書で解り易そうな本を物色し，物理を学ぶには，微積分がいるらしいという事で，数学に手を出し.....，というような状況で，誰に聴く事もできずに悶々とした日々をすごしました．

現在でも，物理を直接に専門にしないまでも，その周辺分野で物理を必要とする方とか，色々な環境のもと，物理の問題を解く為に苦労している人々が多いのではないかと思います．

＞とんでもない誤解をしていてもかまいません．それを見れば「違うよ！」と言うことが出来るのです．

そうですよね，「とんでもない誤解」は「とても素晴らしい理解」に繋がる過程の一つだと思います．それを恥ずかしがらずに質問時に書くと，質問者ご自身の考え方の変遷が身に付くと思います．とは言え，そのようなフランクな質問はなかなか書き込めないのだろうと，感じてしまいます．

＞（問１は高校レベルの問題ですから標準的な回答の仕方は決まっています．問２はちょっと難しいです．）

自分ではまだ直接に解いていませんが，少なくとも水中に半没するような問題を始めて拝見しました．問２も，ちょっと考えないと状況をイメージできませんでした．ちょっと毛色が違う問題だという印象がありました．

ｗｗｗさん，まだご覧になっていれば，ぜひとも質問を続行されませんか？

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/27(Wed) 09:38)

ｍＮｅｊｉさん

一度問題を解いてみてください．

「問２は難しい」と書きました．

計算が難しいわけではありません． 状況が難しいのです．

水面となす角度θについてθ→π／２とθ＝π／２とがつながりません．不連続なんです．（θ＝π／２の位置は不安定な釣りあいの位置です．）

床の上においてある棒の場合でも同じ不連続が起こります．棒の場合は太さを考えると解消出来ますが水に浮いている棒の場合は解消できないように思います．

mNeji さんのレス (2008/08/27(Wed) 13:14)

では，ｋｏｍａｇａｔａｋｅさんのお話に沿って，少し論議を進めてみます．

先ずは，状況の図を書きます．このとき，重要そうな点に解り易い命名をしておきます． <pre>

張力： T↑

・A

／｜ ／｜h＝AC，sin(θ)=AC/AW = h/(L-l) 棒の水面位置：W ／θ｜ 〜〜〜〜〜〜〜〜〜〜〜〜〜＋〜〜〜・〜〜〜〜〜〜〜〜〜水面 ／ C：Aから水面へ下ろした垂線と水面の交点 重力 : F_G ↓／

● G：重心＝重力の作用中心＝ABの中心

浮力 : F_H ↑／

○ H：浮心＝浮力の作用中心＝WBの中心

／ ／ ／ ／ ・B

ーーーーーーーーーーーーーーーーーーーーーーーー 此処で，L＝AB, l=WBとすると，重心と浮心； BG＝GA＝BA/2＝L/2 BH＝HW=BW/2＝l/2 </pre>

先ず棒に加わる力は張力，重力，浮力です．いま棒の断面積を 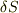としますが，十分に細いとします(浮力を考え易くしてみました)．ここで比重については題意より条件が有るので，合わせて示すと，

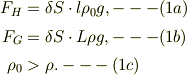
糸を上方に引っ張って静止安定する条件は，先ず「棒に加わる力の平衡の式」；

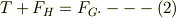
「棒に加わるトルクの平衡の式」を点Aに付いて考えます．なお反時計方向に正の値としますと；

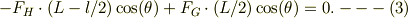
上式で 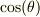が各項で共通だから消去し，(1)を代入して，同様に共通項を整理すると；

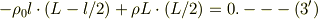
この式は，未知数lだけの式なので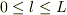， である事に注意して2次式を解けば，

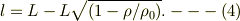
従って，問い(1)について，

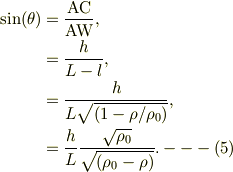
そこで，問い(2)については，式(5)の左辺，右辺で別々に極限を考えます；

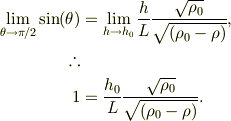
結局，

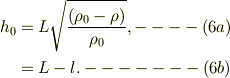
そこで点Aの高さが 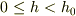の範囲では，棒の角度は 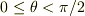のどこでも，式(4),(5)が成り立つ．このとき，張力Tを式(2)について求めておくと，

問題の条件式(1c)より，張力は，常に一定で正の値を持つ．

次に，点Aの高さが 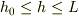の範囲では，棒の角度は 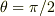となるので，トルクは発生出来ないので，力の平衡だけで決まる．いまTをhの関数と見なすと；

これは下端では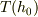， は，(7a,b)に一致し，hの上昇とともに増加して，終点では

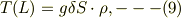
となり棒の全荷重に等しくなる．

従って，張力をhの関数として描くと， <pre> T ｜ ｜ 式(9) ｜・ーーーーーーーーーー ｜／ ｜／ ｜／ ｜／ 式(8) ｜／ ｜／ ｜式(7b)／ ・ーーーーーーーー・ ｜ ｜ ＋ーーーーーーーー・ーーーーーーー・ーーーーーーーーーー h 0h_0 L

</pre>

mNeji さんのレス (2008/08/27(Wed) 16:45)

ｋｏｍａｇａｔａｋｅさんに質問します．

＞水面となす角度θについてθ→π／２とθ＝π／２とがつながりません．不連続なんです．（θ＝π／２の位置は不安定な釣りあいの位置です．）

この点について，式からご説明くださいますか？特に， ・不連続 ・不安定な釣り合い に付いて，知りたい所です．

また正解をご存知でしたら，お教え下さいませんか．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/27(Wed) 17:46)

ｍＮｅｊｉさん

ていねいに解かれましたね．感心しました．

求められた式（５）から

Ｌ−ｌ＝ｈ/ｓｉｎθ＝Ｌ√((ρｏ−ρ)/ρｏ）＝一定

が出てきます．沈んでいる部分の長さ（浮かんでいる部分の長さ）は一定です． この時，張力のＴも一定です．

棒が鉛直になってつりあっているとします． 浮力＝重力とすると

ρo(Ｌ−ｈo)＝ρＬ ｈo＝L(ρo−ρ)/ρo

です．この時Ｔ＝０です．

θ＝π/２で不連続になっているという結果が出てきました． 問２でどういう答えを要求しているのかが分からなくなります．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/27(Wed) 19:08)

ｍＮｅｊｉさん

すみません．中断していました．

不連続，不安定な釣りあい の続きを書きます．

不連続と書きました． 実はθ＝π／２でｈo，Ｔが不定になります． ０≦Ｔ≦Ｍｇ の範囲でつりあうことが出来ます．それに伴ってｈoも Ｌ(ρo−ρ)/ρo≦ｈo≦Ｌ の範囲で変わります． 棒が鉛直に立っているとしてつりあいの条件を求めると解が求められます．したがってつりあいの状態は存在します．でもこのつりあいは揺らぎに対しての復元力がありませんので少しでも傾くと問１で考えた状態に移ってしまいます． ρo＞ρの時，(ρo−ρ)/ρo＜√((ρo−ρ)/ρo)ですから，あるＴのところでつりあっていたとしても少し浮き上がって傾くことでθ＜π／２の状態に移ることが出来るのです．ｈo≧Ｌ√((ρo−ρ)/ρo）になると安定なつりあいになると思います．

安定な釣りあいという条件をつけてもθ＝π/２でｈoは不定になります．

mNeji さんのレス (2008/08/28(Thu) 00:09)

ｋｏｍａｇａｔａｋｅさん，スポーツ・ジムで運動をしていて遅れました．

運動しながら考えたのですが，垂直の場合には，トルク平衡の式はある意味，無意味にあるように思えて来ました．

お説も含めて，しばし考えさせて下さい．この問題は，なかなか面白い問題ですね．なんとか理解したいものです．

mNeji さんのレス (2008/08/29(Fri) 01:00)

ｋｏｍａｇａｔａｋｅさん，遅ればせながら，宿題を整理して，以前の計算，No.21390に追加してみました．特に張力に非連続が起こるとは思えないようでが，如何でしょうか．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/29(Fri) 06:37)

ｍＮｅｊｉさん

私がＮｏ２１３９９に書いたのと同じ結果がでてきましたね． そこで「不連続」というよりは「不定」だと書いたのですが．

「棒が鉛直になったとき」というのをθ→π/2の極限で考えるというのであればＴ＝一定のままです．水面から出ている棒の長さも変わりません．

「θ＝π/2のときのＴ，ｈo」と読むと「鉛直でつりあっているときのＴとｈoとしてもいい」と普通は考えます．そのときはＴとｈoは決まりません．不定になると書いたのはこの意味です．

ｍＮｅｊｉさんも求められたようにhoは Ｌ√(ρo−ρ)/ρo≦ｈo≦Ｌ の範囲で変わります．どこでもつりあいます．Ｔも変わります． この範囲は安定な釣り合いです．揺らぎに対して復元力があります．

棒が鉛直に立っているとしてつりあいの条件を求めるともっと広い範囲の解が得られます． ０≦Ｔ≦Ｍｇ Ｌ(ρo−ρ)/ρo≦ｈo≦Ｌ の範囲です．

Ｌ(ρo−ρ)/ρo≦ｈo＜Ｌ√((ρo−ρ)/ρo) の範囲は不安定な釣り合いです．揺らぎに対して復元力がありません．

以上がこの質問と同じものが出ていたサイトでのやり取りを見ていて考えたことです．それで床の上にある棒の場合，角柱の場合も考えてみました． 浮いている直方体の安定条件も考えてみましたが得られた式にまだ確信が持てないという現状です．

mNeji さんのレス (2008/08/29(Fri) 08:49)

ｋｏｍａｇａｔａｋｅさん，判らない点をお聴きします．

＞「棒が鉛直になったとき」というのをθ→π/2の極限で考えるというのであればＴ＝一定のままです．水面から出ている棒の長さも変わりません．

これはそうだと思います．でも，ゆっくりと糸を張力T＋εで引き上げて行けば，hなりθを増加できますし，糸を張力Tーεで引き下げて行けばその逆もできます．

＞「θ＝π/2のときのＴ，ｈo」と読むと「鉛直でつりあっているときのＴとｈoとしてもいい」と普通は考えます．そのときはＴとｈoは決まりません．不定になると書いたのはこの意味です．

この「Ｔとｈoは決まりません．不定になる」は式ではどうなるのでしょうか．

＞棒が鉛直に立っているとしてつりあいの条件を求めるともっと広い範囲の解が得られます． ＞０≦Ｔ≦Ｍｇ

これは，糸を水中に向かって下げて行く場合の論議でしょうか．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/29(Fri) 10:58)

ｍＮｅｊｉさん

水の中にある棒に糸をつけて上向きに力Ｔを加える． 棒が鉛直に立っている状態でつりあっているとき，力Ｔを求めよ．

という問題だとします．

０≦Ｔ≦Ｍｇ の範囲でどこでもつりあいます． それに伴って水面より上に出ている棒の長さも Ｌ√(１−ρ/ρo)≦ｈｏ≦Ｌ の範囲で変わります．

不定と言ったのはこの意味なんですが． 上で書いたことと同じ内容の繰り返しになっています．

もちろんＴを与えるとｈoは決まります．

mNeji さんのレス (2008/08/29(Fri) 11:35)

ｋｏｍａｇａｔａｋｅさん，

この問題を素直に読めば，初めに水上に横たわって浮いている棒の片方の一点に糸をつけて引き上げる場合の「釣り合いの問題」だと思います．従って，「0 <= h」の挙動が判ればそれで十分だとおもいます．

なお，θ＝π／２の場合，「トルクの平衡」が意味を持たないという事を，「不定」と表現されているのかと思っていました．なお，θ＝π／２の場合でも「力の平衡」は常に成立しているので，張力の連続性が保証されているのだと解釈します．

ｗｗｗさん，

面白い質問を書き込み下さって有り難うございました．水泳での浮き身の計算をしていたので，簡単に解けると思っていたのに，意外と手間を取ってしまいました．

始めには，水の上に横たわっていた棒が，糸で引張りあげる瞬間に，一定部分が水面に出て，一定の張力が高さh(角度θ)を保持する為に必要となるのを納得するのに時間がかかりました．

その意味では，逆に水中に引き下げる場合の計算をしてみると面白そうです．

＃私はと言えば，これ以上の計算はしたくない，という所ですが．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/29(Fri) 18:57)

ｍＮｅｊｉさん

θ＝π/2が物理的にどういう状態に対応するのかを考えるのは大事なことではないでしょうか． こういう風に聞かれたらこう答えたらいいというだけであれば解法のテクニックだけになってしまいます．

私がこの問題を考え出したきかけは 釣り合いが成り立っているとしてＴ＝０を解として求めている回答を見たからです． 初めは「そんな解があるのか?」と思いました． でも「棒が鉛直になってつりあっている」とすれば普通の浮力の釣り合いの問題です．モーメントも何もいりません．一番簡単な解です． そこでさらにつりあいの条件を考えてみました．θ＝π/2に持って行った後Ｔをかなりの範囲で変えることができるのです．Ｔ＝０にしてもつりあっています． Ｔ＝０という解が間違っているとして退ける理由はないはずです．

これはあくまでも静力学の範囲の問題ですからθ→π/2と言ってもこの範囲での回転運動を考えているのではありません．「θの値ごとにつりあいを考えるということをθ＝π/2についてもやったら」という意味のはずです．当然いきなりθ＝π/2で釣り合いを考えるという発想は出てきます．普通はどちらでやっても同じになるのです．違うかもしれないという場面は普通出てこないのです．でもこの問題では違います．いきなりθ＝π/2で考えたものとθ＜π/2から考えたものとが一致しないのです．

そこで出題者はどこまで考えて出したのだろうかと思ったのです．

定期テストの問題として出せば必ず両方の答えが出てくるはずです．入試問題で出ても両方の答えが出て来ると思います．片方だけが正解であるとするのだろうか，もしそうなら両方の答えが出ないようなあいまいさのない表現にしなければいけないはずだと考えました． 私は高等学校で物理を教えていましたからこういうのは気になります．どう表現を変えれば「いきなりθ＝π/2の釣り合いを考えてはいけない」ということを分からせる文章になるのでしょうか．私はすぐには思いつきません． こういう問題は出して欲しくないという思いです．でもこういう食い違いに気のつかない出題者であれば文章を工夫するなんて考えは出てこないでしょう．多分Ｔ＝０はアウトにするのでしょう．解法のテクニックが強調される事になります．

もう1つ気になりました． θ＜π/2の時，Ｔ＝一定です．これは机の上の棒に紐をつけて持ち上げるという場合でも同じになります． でもこの棒についての結果は日常経験することと合いません．傾いている重いものを支える時，傾きが小さければ小さい力ですむというのが普通に経験することです．力をどの方向に加えているかにはあまり関係しません．少しでも傾けばいきなり大きな力がかかるというのは不思議な結果です． これは棒の太さを考えに入れると解消できることが分かりました．傾きを小さくすれば力が小さくなり，ある角度でＴ＝０になります．連続的にＴ＝０になるのです．力を斜めに加えるということでも解消できます．でもこの時は床との摩擦が必要になります．浮力の場合は摩擦を考えるわけにはいきませんので鉛直方向の力しか考えることが出来ません．

mNeji さんのレス (2008/08/29(Fri) 20:04)

ｋｏｍａｇａｔａｋｅさん，

漸くご主張の事が判りました．でも，問題にある条件；

＞糸を張力0からゆっくり力を加えて引き上げる．

からすると，考慮する必要は無いとおもいます．

すなわちこの問題では，No.21390の最後の図，(T-h)特性の原点h=0から右に向かって進行する，すなわち「ゆっくり力を加えて引き上げる．」と書いてあるからです．

実際的に，お書きになっている状況を作るには，少なくともhがh_0を越えるところまで引き上げた上で，左右方向の力が発生させないように「ゆっくりと力を抜きながら下げて行く」必要があります．念の為に図示すると，本文で示されている初期条件から「静的に平衡した状態を経由して垂直に立ち，張力がゼロ」に到達するには，下図で示すα状態から始まり，角度が変化しながらβ状態に至り，角度がπ/2に達したら，角度を厳密にπ/2に保ちながらδ状態へ降下する必要があります．もしβ→δの移動中に角度に変化を生じると静的平衡は壊れて，動的状態に遷移します．

<pre> T ｜ ｜ 式(9) ｜γ・ーー ｜／ ｜／ ｜／ ｜／ 式(8) ｜／ ｜／ ｜式(7b)／ α・ーーーーーーーー・β ｜ ／ ｜／ ＋ーーーーー・ーー・ーーーーーーー・ー h 0 δ h_0 L

</pre>

この時には「θ＝π/2」なので「トルクの平衡」は意味をなさないので，「力の平衡」だけで決まるので，T＝０に達するまで下げる事は出来ます．しかし，少しでも左右方向の力が入れば，棒は水平に浮き上がってしまうでしょう．

この事は，プールで「ヌードル」と呼ばれる長さ1.5mぐらいで，直径10cmぐらいの棒(恐らく，発泡ポリ・スチロール)を水中に沈める時にも体験します．今回の計算でも，「θ→π/2」と「θ＝π/2」の意味の違いは正確に論議したつもりです．

むしろ，もう少し詳しく論ずるべきは「θ＝ゼロ」の近傍の振るまいかも知れません．おそらく棒が有限の直径を持つ効果が出て来るだろうと思うからです．そうすると，「T＝０」からの図が書けと筈です．ただ，マイナーの事だろうと思ってかきませんでしたが，初期にはかなり気になっていました．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/29(Fri) 21:44)

ｍＮｅｊｉさん

＞ゆっくり力を加えて引き上げる

Ｌ√(１−ρ/ρo)≦ｈo≦Ｌ はどうなります．どこでもつりあいますよ．

ずっとほぼ一定の力を加えてきてθ＝π/2のところで急にどんな力でもつりあうということになるのですから「あれっ！」と思う状況ではないですか．

静力学の範囲を超えて動きを意識しているのであれば無限小に逃げ込むのは適当ではありません．１割大きい力で動かしたのであればその１割大きいままの力でつりあうのです．（普通のつりあいの問題でもつりあいの状態に持っていくには余分の力が必要です．でもつりあいの状態はたいてい１つしかありませんから余分に加えた力は考えから外してしまっているのです．）

θの値ごとにつりあいを実現させていくという静力学の立場であればθ＝π/2でのつりあいをいきなり考えることもありです．

mNeji さんのレス (2008/08/30(Sat) 00:37)

ｋｏｍａｇａｔａｋｅさん，

＞＞ゆっくり力を加えて引き上げる

「ゆっくり力を加えて引き上げる」というのは，「準静的に引き上げる」という方が正確かも知れません．当然，静止する事を含んでいると思います．でも「ゆっくりと力を抜きながら下げて行く」という概念までは包括するとは思えません．勿論，問題を拡大解釈するのなら別の問題となるのでしょうね．

＞Ｌ√(１−ρ/ρo)≦ｈo≦Ｌ ＞はどうなります．どこでもつりあいますよ．

この部分は，なにを仰りたいのか理解出来ません．私の計算した結果から類似の関係式を検討しますと，以下の様になります；

問題から与えられたのは，始めに水面に浮かんだA点が水面から垂直に引き上げられた高さをhとしているので，この範囲は原理的には；

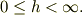
であると思いますが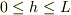， としても良いとは思います．

ただし，トルク平衡の式で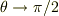， の極限とした時に， に接近し；

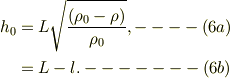
となります．これは 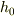の定義式であり，等号で書いてあります．問題の水と棒の密度の関係式(1c)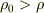， から，

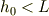
となります．この 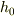の状態から，完全に 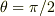に移動した瞬間に，トルク平衡の式は意味を失い，力の平衡だけで「糸が上昇する」と解釈します．

ところが，「Ｌ√(１−ρ/ρo)≦ｈo≦Ｌ」という式の意味を汲み取る事ができません．例えば，全てを等号とすると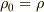， という結果となってしまい，題意に反しています．

＞θの値ごとにつりあいを実現させていくという静力学の立場であればθ＝π/2でのつりあいをいきなり考えることもありです．

冒頭の話に戻っていますね．問題を捉え直すということなら，お説の考え方も在り得ると思います．例えば，h=Lの状態から，ゆっくりと力を抜きながら下げて行くときに，糸に掛かる張力と，平衡条件を論ぜよ，とかするのでしょうか．

〜〜〜〜 本問題にたいする私の解答は完結したと思います．まだ間違いもある可能性は否定しません．

そこで，ｋｏｍａｇａｔａｋｅさんのお考えの「模範解答」をお教え下さると有難いです．

また，宜しければ，既に論議がされたサイトをご紹介下さると勉強になると思います．

mNeji さんのレス (2008/08/30(Sat) 13:14)

持ち合わせの木の角材で試して見ました．

その木材は，0.6cm角x19.5cm程で，重さ4g(料理計りの為，分解能1g)．

従って，

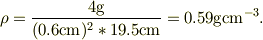
No.21390の式(6a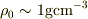)で， として，

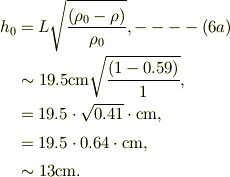
洗面の所で，数十度程度に吊って見ると，水面上に出ている部分の位置は概略あっているようでした．

理科室を借りて，「hないしθを変えながら張力を測る実験」でもすると面白いかも知れません．

また，ｋｏｍａｇａｔａｋｅさんの仰っている垂直で，張力ゼロの実験をするのも良いとおもいますが，実験に工夫を要するとおもいます．参考までに，そのとき，水上に出ている部分の式は，

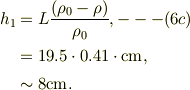
追伸：

計算結果を棒に書き込んで，定性的な振る舞いを確認してみました；

（１）角度を0°から90°に向けて行くと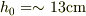， の前後±5mmぐらいに入っている様でした．

（２）90°に接近してくると，糸が棒に対して角度を持って来る為に，素直に上方に引き上げられませんでした．現在は，糸を側面で縛っただけですので，接着材で固定する様にしようかと思いました．

（３）ただし，何遍もトライしているうち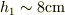， に近くまで下がった事があります．

（４）物理実験というと，判り切った事を測定し，目的の値と違った場合の考察で頭を悩ませる，といったイメージでした．今回の場合，問題を解いた上で，その正当性を確認するという，積極的な意識のもとに実験出来たのが良かったですね．

（５）しかし，定量的な実験となると，なかなか個人レベルでは，実行が難しくなります．中学・高校の理科室を，高齢者の脳活性化と学生さん達の深い学力増強の為に，公開してみると面白いかも知れませんね．