おっとっと さんの書込 (2008/08/21(Thu) 04:13)

弾性散乱において，角運動量で部分波展開するときの質問です．

波数|k|が一定→エネルギーが一定→運動量pが一定

ということは，角運動量l=r×pで展開するということは， 運動量の方は，|hk|=|p|で一定だから， 衝突パラメータで展開するということなのでしょうか？？

波数ｋの状態の散乱を扱っているのに， 角運動量で展開できる理由がいまいちわからないんですが．

また，弾性散乱で，標的粒子が重い場合で， 入射粒子のエネルギーは散乱後と変わらないとします． その際，入射前と散乱後で角運動量Lが変わる場合， それは衝突パラメータが変化しているからだと考えてよいのでしょうか？ でも教授にそう答えたら違うといわれてしまったのですが．．．

ごちゃごちゃしててすみません． 一つ目の質問だけでもよいので，どなたかアドバイス下されば助かります．

おっとっと さんのレス (2008/08/21(Thu) 04:29)

すみません，追記です．

一つ目の質問は， スピンを考慮しない場合の量子力学の本に書いてあることについての一般的な質問です．

二つ目の質問は，私は，「弾性」散乱の際に，スピン部分だけでは保存せず， スピンと軌道角運動量の和が保存している問題を扱っています． その際，スピン部分が変化して，軌道角運動量が変化する現象を扱っています．「エネルギーは変わらないのに，角運動量が変わるというのはどういうことか？」という質問を受けたのです．

たびたびすみませんが，よろしくお願いいたします．

おっとっと さんのレス (2008/08/21(Thu) 05:16)

度々，ごめんなさい＞＜

二つ目の質問ですが，標的粒子については，「何も」変わりません．

mNeji さんのレス (2008/08/21(Thu) 09:20)

おっとっとさん，初めまして．

詳しい説明はできませんが...．

(1)角運動量で部分波展開

＞波数|k|が一定→エネルギーが一定→運動量pが一定 (略) ＞衝突パラメータで展開するということなのでしょうか？？

概ね，そのように考えたので良いと思います．

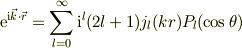
ここで，θは 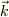と 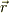の成す角度．

ですよね．

＃量子力学の本を持っていないので，電磁気の本から書き写しましたが...． ＃一度，ルジャンドル関数の係数部分を，krの関数として，l=0..3ぐらいについて，プロットしておくと良いかも知れませんね．

(2)「エネルギーは変わらないのに，角運動量が変わるというのはどういうことか？」

軌道角運動量とスピンとの結合が弱くて(ないしは無くて)，スピンの方向に依らず準位のエネルギ値が縮退しているから，としか言えないような気がします．

むしろスピンの反転がエネルギ変化なしに起こるメカニズムを検討しろとでも言うのでしょうかね．そうだと，難しいかな...．

nomercy さんのレス (2008/08/21(Thu) 09:35)

二つ目についてですが， 標的粒子と散乱される粒子はどのような相互作用をしているのですか？

yama さんのレス (2008/08/21(Thu) 11:36)

最初の質問ですが，量子論では確定した軌道が存在しないので，古典論のような衝突パラメータを考えることはできません． そのかわりに角運動量を考えるのだと思います． 古典的極限を考えれば，衝突パラメータを用いるのと同じことになるでしょう．

２番目の質問は，スピン軌道相互作用がある場合ではないでしょうか． いずれにしても，古典論でも衝突パラメータが衝突によって変化することはない（というよりも意味がない）と思いますし，量子論では衝突パラメータを考えること自体が無意味だと思います．

おっとっと さんのレス (2008/08/21(Thu) 19:12)

皆様ご回答どうもありがとうございます． ご回答の内容が，重なる部分と食い違っている部分があるようなので， まとめて返信致します．

「波数ｋという状態が決まっている」のにもかかわらず， 角運動量r×pで展開しているということは， kと一対一の関係にあるpでは展開できないはずだと思いました． kとｐは同時固有状態ですし・・・． そこで，rに依存する衝突パラメータで展開しているのか？ もしくは展開できないんじゃ？と疑問を持ったわけです． 衝突パラメータで展開していないとしたら，いったい何で展開しているのでしょう？？

相互作用については，言った方が良いかとお答えしやすくなるとは思うのですが， 研究内容で明かしたらまずいかと思いまして， 申し訳ないのですが，控えさせて下さい．ごめんなさい．

いずれにせよ，衝突の際にある相互作用で入射粒子がスピン反転し， 結果，軌道角運動量も変化します． この軌道角運動量の変化と，エネルギーが変わらないことの矛盾？は， 衝突パラメータを考えることが無意味ならば， 量子論的にはどう説明できるのでしょうか．．．？？

おっとっと さんのレス (2008/08/21(Thu) 19:20)

＞mNejiさん

すみません，衝突パラメーターで展開しているので概ね正しいとのことですが， そうではないというyamaさんの意見もありましたので， yamaさんよりの返信になってしまいました．

ところで，散乱される粒子のエネルギーは，スピン反転では， ほとんど変化しない理由はわかっています． （微細構造とかでもエネルギーの差が微弱ですので）

スピンの方はエネルギーがほとんど変化しないので理解できるのですが， 軌道角運動量の方は，エネルギーが変化してしまい， 弾性散乱と矛盾してしまうという疑問です． しかし，弾性散乱なのです．．その疑問を解決してこいってことで困ってます．

yama さんのレス (2008/08/21(Thu) 20:27)

運動量が一定の状態は，運動量の固有関数で表されますが，その固有関数を角運動量の固有関数で展開するということだと思います．

>この軌道角運動量の変化と，エネルギーが変わらないことの矛盾？は， >衝突パラメータを考えることが無意味ならば， >量子論的にはどう説明できるのでしょうか．．．？？

矛盾ではないと思います． エネルギーと同時に保存するのは，全角運動量（軌道角運動量＋スピン角運動量）であって，軌道角運動量だけでは一般には保存しません．

おっとっと さんのレス (2008/08/21(Thu) 20:51)

yamaさん

ご返信，どうもありがとうございます．

一つ目について，とても納得致しました．

度々質問で恐縮なのですが，二つ目について， 軌道角運動量L＝r×pという式を考えた場合， 軌道角運動量L＝r×pで，エネルギー一定 →pが一定，なのにもかかわらず， Lが変化するのはどういうことでしょうか？ rが変化しているからでしょうか？しかし，衝突パラメータは関係ないとのことですが．．

スピンが変化しているから，というのはわかるのですが， r×pという式に着目すると，意味がよくわからくなってしまうのです．

yama さんのレス (2008/08/21(Thu) 22:14)

軌道角運動量と運動量の共通の固有関数というものはありません． 従って，軌道角運動量と運動量が同時に確定値をとることはありません．これは交換関係からも明らかです． たとえば軌道角運動量とエネルギーが一定値をとる場合は，運動量は確定値をとりません． また，運動量とエネルギーが一定値をとる場合は，軌道角運動量は確定値をとりません．

mNeji さんのレス (2008/08/21(Thu) 23:43)

＞すみません，衝突パラメーターで展開しているので概ね正しいとのことですが， ＞そうではないというyamaさんの意見もありましたので，

イメージとして，入射平面波を軌道角運動量の固有状態として展開出来ると理解しています．私の理解では，運動量固有値に拘る必要はないように思います．むしろ，「平面波でも角運動量を持ち込む事ができる」のが大切とおもいます．

他方，

＞ところで，散乱される粒子のエネルギーは，スピン反転では， ＞ほとんど変化しない理由はわかっています．

という部分と，次の

＞スピンの方はエネルギーがほとんど変化しないので理解できるのですが， ＞軌道角運動量の方は，エネルギーが変化してしまい， ＞弾性散乱と矛盾してしまうという疑問です．

という部分とが両立すると言うのは，理解出来ません．

でも，これらの点を論議しようとすると，実験の詳細や，解析手段などの論議になりますね．ところが，現在進行中の実験だとすると，このような公開サイトで論議するのは如何なものかと感じます．

おっとっと さんのレス (2008/08/22(Fri) 01:16)

＞yamaさん

あーそっか．．．エネルギーと同時に，って所がいまいちわかっていませんでしたが，固有関数という言葉で理解できました．どうもありがとうございます． 二度同じことを言わせてしまったようで，でも丁寧にご回答下さりありがとうございました．

＞mNejiさん 一般的なお話ですよ． おっしゃる通り，固有状態にこだわり過ぎてはいました． 平面波を展開できるという考えが重要なんですね． どうもありがとうございました．