03年11月東大即応オープン
03年11月東大即応オープン
ゆうや さんの書込 (2008/08/18(Mon) 20:29)
高3です．03年11月の東大即応オープン第1問で質問です．
質量Mの地球の中心から距離rの円軌道上を，質量が共にmの宇宙船A,Bが同じ向きに同じ速さvで回っている． ただし，宇宙船は地球からの万有引力のみを受けて運動するものとする． また地球は密度が一様な球体とし，万有引力定数をGとする．
まず，地球の周りを楕円軌道を描いて回る質量mの宇宙船の運動について一般的に考察しておこう．楕円の長半径をa，地球の中心から軌道上の近地点Pまでの距離をr 1 ，遠地点Qまでの距離をr 2 とする． (1)宇宙船の力学的エネルギーEを表せ．（←これはいいです．） (2)宇宙船の面積速度をsとするとき，E,G,M,m,sを用いてr 1 ,r 2 が解となるrの2次方程式を導け．・・・
2次方程式が分かりません． 最初は，和，積が表せればと考えたのですが，表せず，行き詰ってしまいました． なにかヒントをお願いします．
Re: 03年11月東大即応オープン
toorisugari no Hiro さんのレス (2008/08/18(Mon) 20:48)
面積速度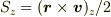 
は軌道上で保存し，近地点，遠地点では単なる積 
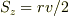になります．これと(1)とを絡めれば解けるのでは?
