院試の勉強で困ってます．

院試の勉強で困ってます．

大学4年生です． さんの書込 (2008/08/17(Sun) 23:52)

はじめまして．院試の勉強をしている大学四年生です．

数学のある問題を解いてみたのですが，どうしても答えと合いません． お時間がある方，間違いの指摘や，できれば正しい解答を載せて頂けたら幸いです．

次に問題を示します．(参考文献：詳解大学院への数学東京図書より抜粋しました．)

曲面 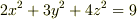2x^2+3y^2+4z^2=9 について，この曲面で囲まれた部分の体積を求めよ．答えは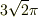 3\sqrt{2} \pi

僕の解答としては，

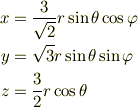
x &=\frac{3}{\sqrt{2}}r\sin \theta \cos \varphi \\y &=\sqrt{3} r \sin \theta \sin \varphi \\z &=\frac{3}{2}r \cos \theta

と変数変換を行い． 体積 V を

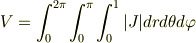
V=\int_0^{2\pi} \int_0^\pi \int_0^1 |J| drd \theta d \varphi

として計算しました． ここで，ヤコビアン 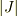|J| は定義に従い．

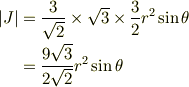
|J| &=\frac{3}{\sqrt{2}} \times \sqrt{3} \times \frac{3}{2}r^2 \sin \theta\\&=\frac{9\sqrt{3}}{2\sqrt{2}}r^2 \sin \theta

というようになりました．

V を計算すると

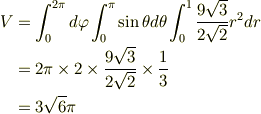
V &=\int_0^{2\pi}d \varphi \int_0^\pi \sin \theta d \theta \int_0^1 \frac{9\sqrt{3}}{2\sqrt{2}}r^2 dr \\&=2\pi \times 2 \times \frac{9\sqrt{3}}{2\sqrt{2}} \times \frac{1}{3}\\&=3\sqrt{6} \pi

となって参考書の解答と合いません． 楕円の問題だと思ったのですが違うのでしょうか？どなたかご教授願います．

Re: 院試の勉強で困ってます．

yama さんのレス (2008/08/18(Mon) 00:19)

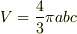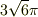楕円体の問題ですね． 楕円体の体積の公式 V=\frac{4}{3}\pi abc を用いても 3\sqrt 6\pi になるようですから，参考書の解答が間違っていると思います．

Re: 院試の勉強で困ってます．

大学4年生です． さんのレス (2008/08/18(Mon) 00:25)

解答ありがとうございます． 楕円体の体積の公式の存在を知りませんでした．

公式をちゃんと調べていれば，解決できていた問題だったようです．

お時間とらせて申し訳ありませんでした．

Re: 院試の勉強で困ってます．

yama さんのレス (2008/08/18(Mon) 09:10)

楕円体の体積の公式を知らないとしても，球の体積の公式は知っているものと思います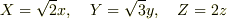． X=\sqrt2x,\quad Y=\sqrt 3y,\quad Z=2z と置くと，体積は次の式で計算できます．

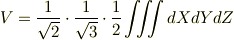
V=\frac{1}{\sqrt2}\cdot\frac{1}{\sqrt3}\cdot\frac{1}{2}\iiint dXdYdZ

積分の範囲は 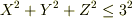X^2+Y^2+Z^2\le 3^2 なので，球の体積の公式を用いると簡単な計算で 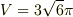V=3\sqrt6\pi が得られます．

１つの方法だけでなく，いろいろな方法を考えることが大切だと思います．

Re: 院試の勉強で困ってます．

mNeji さんのレス (2008/08/18(Mon) 10:07)

横から失礼します．

＞１つの方法だけでなく，いろいろな方法を考えることが大切だと思います．

yamaさんのご意見は，とても味わい深いとおもいます．

他方，「大学4年生です．」さんは指力がおありだと思うので，直感的な方法とか，すこし角度を変えた方法などにトライしておくと更に力が付くと思います．自分で，自分にクイズを出すような感じかも．