けん（大学3年） さんの書込 (2008/08/17(Sun) 22:42)

流体力学の質問です．

至る所で密度が一定の完全流体の定常的で２次元的な流れを考えます．外力はないとします．

速度vで流れている流体のすぐ隣の流体がそれより大きな速度で流れている場合，速度が大きいところの方が速度が小さいところよりも圧力が小さいということがベルヌイの定理から導けますが，現象として直感的に納得できません．直感的に，イメージを持って理解するための考え方を教えていただきたいです．よろしくお願いします．

toorisugari no Hiro さんのレス (2008/08/18(Mon) 14:06)

非圧縮非粘性流体なら流体粒子の加速度は

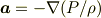
で記述できます．右辺括弧を単位質量あたりのポテンシャルと見なせば，ベルヌーイの法則は「保存力に対する力学的エネルギー保存則」にほかなりません．

流れに乗って速度が大きくなるなら加速度が発生しているはずです．すると運動方程式から力が発生しなければいけません．この力は流体粒子の両側にかかる圧力の差から発生します．つまり，速度の大きくなる方向に圧力が小さくならないと加速度は発生しないのです．

ポテンシャルで考えれば，速度の増す方へポテンシャル＝圧力は小さくなることから同じ結論になります．

けん(大学3年) さんのレス (2008/08/18(Mon) 17:57)

解説ありがとうございます．

＞速度の大きくなる方向に圧力は小さくならないと加速度が発生しないのです

特殊な状況を考えます． 流れている２次元平面をxy平面とします． 上の仮定に加え，y=0,hに壁があり，流体はその間にのみ存在するとします．系はx方向に平行移動しても変わらないとします．位置(x,y)における流体の速度ベクトルをv=(v(y),0)とします．（仮定からxにはよらない）．もし一方の壁が速さUでx方向に流れているとすると，速度はyにより，かつy軸方向には流れはありません．この場合でも「速度が大きいところの方が速度が小さいところよりも圧力が小さいということがベルヌイの定理から導けます」が，y方向に流れのないこの場合でもtoorisugari no Hiroさんの書かれた解釈は使えるでしょうか．y方向に流れのないことからy方向には加速度は生じません． よろしくお願いします．

toorisugari no Hiro さんのレス (2008/08/18(Mon) 20:29)

> 特殊な状況を考えます．

確認しますが，定常非粘性流れですね．粘性があるとベルヌーイの定理は使えません．

> 流体の速度ベクトルをv=(v(y),0)とします．

流線はx軸に平行な直線群になりますね．

> 「速度が大きいところの方が速度が小さいところよりも圧力が小さいということがベルヌイの定理から導けます」

導けません．

異なる流線における圧力はベルヌーイの定理で比較できません．比較できるのは渦なし流れ(上の流れなら「一様流」)のときだけです．(そもそも，流線が異なるなら違う流体粒子で比較する事になるので，エネルギー保存則を使うことはナンセンスですね．)

所詮，ベルヌーイの定理は運動方程式を流線方向に射影したものにすぎないので，一般の場合を考えるなら運動方程式そのものを使うべきです．

# ただし，「流線曲率定理」なら，流線をまたがって使えます．これは運動方程式を流線の曲率方向に射影したものです．

桝岡 さんのレス (2008/08/20(Wed) 08:49)

ベルヌイの定理は， ・流線上に圧力変化があるとき，圧力変化により流れが加速減速される ことを数式で表現したものです．

圧力が低いところから，高いところに流れ込む場合，流れは減速されます． 逆の場合は，流れは加速されます． その結果，流線上で，圧力の高いところでは遅く，低いところでは速い流れが形成されます． 直感的にも，あたりまえのこと，ですよね？

ベルヌイの定理を直感的に納得できない，と感じるのは， ・流速の変化(原因)により，圧力の変化(結果)が発生する，と勘違いする ためだと思います． 流速がわかれば，流速から圧力を計算できますが，これは計算手順であって， 物理的な因果関係ではありません．

toorisugari no Hiro さんのレス (2008/08/20(Wed) 14:30)

桝岡さん

> 直感的にも，あたりまえのこと，ですよね？

私もそう思います．ただ，

> 流速がわかれば，流速から圧力を計算できますが，これは計算手順であって，物理的な因果関係ではありません．

これはどうかと思います．

定常な流れの中の流体粒子の運動に限れば，慣れ親しんだ力学的イメージ(力が運動の変化を起こす)にあう「圧力変化により流れが加速減速される」で考えて良いと思います．わたしもこれに従って説明しました．

しかし，支配方程式の構造を考えると，非圧縮性流体においては「速度場が圧力場を決定する」と考えるのが正しいと思います．

非定常な場合，支配方程式に圧力場の時間微分項がないことからも，圧力場の時間変化は速度場の時間変化に「追従」していることがわかります．

定常な場合，支配方程式の数学的構造から説明できますが，簡単のため，もっとも基本的な流れ場である非圧縮・渦なしの流れを考えると，以下のように，圧力場が速度場に「追従」していることがわかります．

この場合，非圧縮・渦なしとういう条件 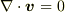, 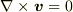により

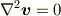
という「ラプラス方程式」が得られます．また，定常・渦なしですから，運動方程式は「流線上」という制限のない「一般化されたベルヌーイの定理(＝圧力方程式)」

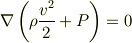
に情報の欠落なく変形されます．

速度場と圧力場が未知で，境界条件だけ与えられているとします．

ベルヌーイの定理からは，速度場と圧力場のどちらも決定できません．しかし，境界条件が決まっていればラプラス方程式は解けてしまい，速度場が決定されます．次にベルヌーイの定理から，速度場を用いて圧力場が決定されます．

つまり，ベルヌーイの定理において，速度場が原因で圧力場が結果です．

「(渦度の分布と)境界条件と非圧縮条件をみたす速度場を維持できるように圧力場が追従する」と考えるのが流体力学的には正しいです．

ただし，流体粒子を考えるとき，つまり，与えられた速度場と圧力場の中を流体粒子が運動してるとき，「圧力変化により流体粒子の速度が加速減速される」は間違いではありません．(既に速度場があるので今更ですが．．．)

桝岡 さんのレス (2008/08/21(Thu) 08:36)

>境界条件が決まっていればラプラス方程式は解けてしまい，速度場が決定されます． >次にベルヌーイの定理から，速度場を用いて圧力場が決定されます．

これも，計算手順であって，物理的な因果関係ではありません．

>「(渦度の分布と)境界条件と非圧縮条件をみたす速度場を維持できるように圧力場が追従する」 >と考えるのが流体力学的には正しいです．

これは，流体力学の体系(物理現象を数式化し，解くためのテクニック)が，そのように構成されているだけで，物理的な因果関係は別です． 支配方程式は，物理的な相互関係を数式化したものですが，物理的な因果関係は不明瞭になっています． それを解くのは，物理的な因果関係とは無関係な，数学的なテクニックに依存します．

実際には，速度と圧力は相互に影響しながら，同時に確定すると思うので， ・圧力変化(原因)により流速が変化(結果)する とも言いにくいのですが，少なくとも， ・流速の変化(原因)により，圧力の変化(結果)が発生する は間違っていると思います．

toorisugari no Hiro さんのレス (2008/08/21(Thu) 13:41)

どうも桝岡さんは，流体が粒子系でなく連続体であること，あるいは流体力学が(非平衡)熱力学に基づいていることを軽視されていらっしゃるように思えます．また，プリミティブな力の概念に固執されているように思えます．

圧力は熱力学的な状態量であり，定数部分をのぞき，外部からコントロールはできません．

圧縮性の流体の場合，圧力は密度の空間分布に依存します(例えば静的近似として「理想気体の等温過程の状態方程式に従う」でかまいません)．そういう意味で圧力は密度に追従します．

この密度の空間非一様性や時間変化を直接担っているのは，速度場，です．すなわち，熱力学的フェーズにおいては 速度→圧力 と観ることができます．

# (古典力学の，外部からコントロール可能な，あるいは，運動を起こす原因となる，「力」という概念は圧力には通用しません．そもそもこのような力の概念はもはや粒子力学に限ってもプリミティブすぎますが．．．)

流体粒子の運動に関しては確かに圧力を力の源，運動の変化を司るもの，と考えることもできます．そういう意味で 力学的フェーズにおいては 圧力→速度 も可能です．

圧縮性流体ではどちらのフェーズも無視できません．ですから圧縮性流体では，速度と圧力に対して，どちらが主で，どちらが従，というのは間違いです．

非圧縮性流体は音速無限大という極限的，理想的，数学的，存在です． # (しかし，多くの実在流体の振る舞いが記述できる概念なので，「非物理的」とは言えません．これは「剛体」が同様の仮定に基づいているが「非物理的」ではないことと同じです．)

「非圧縮性」の仮定は非常に強すぎます．微小の密度変動に対して圧力が大きく変動することの極限が「非圧縮性」なので，熱力学的フェーズはなくなります．また，速度場が発散0になることが密度一定の必要条件ですが，このため，力学的なフェーズは経ずに，粒子の意味でなく場の意味で，速度は決定されてしまいます．すなわち，速度の決定に圧力は必要なく，力学的整合性を満たすため，圧力が追従するしかないのです．

# (ただし，「非圧縮性」を「 密度一定を保つように，[瞬間的に圧力場が全空間で変化して，よって，]速度場が瞬間的に全空間で発散0に調整されること． 」と近似的に捉えるなら，圧力→速度と考えることもできます．でも「非圧縮性」極限では「因果」は消えてしまいます．)

圧力が追従することを「数学的テクニックにすぎない」と無視するの勝手です．しかし，そのときは，「非圧縮性」という概念も使わないでください．

「非圧縮性流体では，直感に反して，圧力は速度に追従するが，これは『非圧縮性』という概念が極限的な概念のための見かけの事象である．」 や 「圧縮性流体の力学的フェーズでは速度場は圧力場に追従する．」 というのはOKですが，

非圧縮性流体では，「速度場は圧力場に追従する．」は間違いですし，「『圧力場は速度場に追従する』という考えはおかしい．」も間違いです．

けん（大学3年） さんのレス (2008/08/22(Fri) 00:42)

toorisugari no Hiroさん，桝岡さん，レスありがとうございます．

＞toorisugari no Hiroさん

＞確認しますが，定常非粘性流れですね．

分かりにくくてすみません．No21303で書いた「上の仮定に加え」とは，No21287の仮定に加え，という意味で書こうとしたものです．（しかし，「流れている２次元平面をxy平面とします．」をさしているように誤解されやすい表現になってしまっています．）

＞toorisugari no Hiroさん，桝岡さん 一様流の話では，ベルヌイの定理の仮定をうっかりしていました．すみません．異なる流線場の，今の場合は特にx座標が同じ2点において，速度の大小関係から圧力の大小関係を直感的に考えることはできるのでしょうか．

toorisugari no Hiro さんのレス (2008/08/22(Fri) 12:06)

> 異なる流線場の，今の場合は特にx座標が同じ2点において，速度の大小関係から圧力の大小関係を直感的に考えることはできるのでしょうか．

非粘性定常流ですね．

「渦なし」でないなら異なる流線上の2点間の圧力を「ベルヌーイの定理」で比較する事はできませんが，「流線曲率定理」なら可能です．

「流線曲率定理」を日本語で言えば 「流線が曲がっているなら，内側(曲率中心側)の圧力は低く，外側の圧力は高くなる．曲率半径方向(流線に垂直)の圧力勾配は速さの2乗に比例し曲率半径に反比例する． 」， 式で書くなら を曲率中心からの距離として

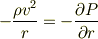
です．

先の問題では流線は直線ですから，曲率半径は無限大，つまり，圧力勾配の流線垂直方向の圧力勾配は0となり，圧力はyに依存しないと言うことになります．

異なる2点の圧力を比べたいときには，流線に垂直な方向には「流線曲率定理」を，流線に平行な方向には「ベルヌーイの定理」を，組み合わせて使えばよいでしょう．

「流線曲率定理」は曲がった流線の一部を円と考えたときの，圧力勾配と遠心力との釣り合いと解釈できます．

流体粒子が(等速)円運動しているとき，加速度は中心方向に発生

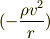
します．その加速度を維持するのは圧力勾配 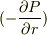です．つまり，内側(曲率中心側)の圧力は低く，外側の圧力は高くなります．

なお，半径に対して(円運動の)速度が増加しようが減少しようが，時計周りだろうが逆回りだろうが，「流線曲率定理」には関係ないことに注意してください．

kei さんのレス (2008/08/22(Fri) 12:50)

横から失礼します．

桝岡さま toorisugari no Hiroさんがおっしゃるように速度場と圧力場を

〉物理的な因果関係とは無関係な，数学的なテクニック

としてしまうのは賛成できません．式の詳細は置いといて流体力学は“流れ”を第1に重要視する領域であると私は認識しています．1つの方程式に“流れ”を表現する速度場と圧力場が含まれるのならば，2つの場が物理的因果関係が無関係ではないと思いますが．境界条件などが設定された問題を解くことは確かに数学的なテクニックであるとは思いますが，これらの式をモデルから数式にする段階で因果関係を考慮しているはずなんで，原理に立ち返ると結局無視できないのではないでしようか？

書き込んでみたものの私は胸を張れるほど流体について学んでいるわけではありません．因果関係というのを“速度場と圧力場の(相互)関係”というように解釈し上のように書いてみましたが桝岡さんの主張される“物理的因果関係”というのがいまいち理解できないです．流体力学の体系が数学的テクニックのみで構成されているとおっしゃるのならば“物理的因果関係”は流体力学のどの部分を司っているのですか？

何をもって“物理的因果関係”なのか，そしてどうすれば圧力場と速度場に物理的因果関係が認めらるのかに興味があります．差し支えなければご教授ください．

トンチンカンな内容になってしまいましたがよろしくお願いします．

toorisugari no Hiro さんのレス (2008/08/22(Fri) 14:03)

えーっとわたしに読解力がないので，どちらに対してのご意見かわからないのですが，

最初のパラグラフ > toorisugari no Hiroさんがおっしゃるように速度場と圧力場を >〉物理的な因果関係とは無関係な，数学的なテクニック >としてしまうのは賛成できません．式の詳細は置いといて流体力学は“流れ”を第1に重要視する領域であると私は認識しています．1つの方程式に“流れ”を表現する速度場と圧力場が含まれるのならば，2つの場が物理的因果関係が無関係ではないと思いますが．境界条件などが設定された問題を解くことは確かに数学的なテクニックであるとは思いますが，これらの式をモデルから数式にする段階で因果関係を考慮しているはずなんで，原理に立ち返ると結局無視できないのではないでしようか？

は 「 流体における速度場と圧力場の間には因果がある． なのに，『非圧縮流体では境界条件とラプラス方程式から圧力場と無関係に速度場が決まる』ことは上の因果を破っているように見え，物理的におかしく思える． しかし，非圧縮極限を採る前を考えれば，圧力場から速度場への因果は見えなくなっているだけで，存在しているのだから，『』の部分をテクニックにすぎないと否定する事はおかしいのではないか? 」 ということでしょうか? #(違ったら訂正してください)

桝岡さんがこれに対してどのようなご意見をお持ちか私にはわかりませんが，私の意見を述べます．

そういう解釈もあると思います(#21334の記事でOKだといった考え方です)．しかし，そもそも，私は「因果」そのものを重要視していません．

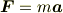
という運動方程式があったときに「力が発生することによって加速度が発生する」というのが，ここで議論されている「因果」だとおもいます．

しかし，私は「加速度が発生することによって力が発生する」という「因果」もありだと思っています． #(この感覚は普通だと思っているのですが違うのでしょうか?)

ですから，「非圧縮流体においては，非圧縮性という拘束条件(と渦度分布と境界条件)により速度場が決まり，(運動方程式を通して)『速度場に圧力場が追従』する」ことに何の違和感もありません．

kei さんのレス (2008/08/22(Fri) 17:02)

〉toorisugari no Hiroさん すいません．打ち始めたところで昼食を挟んでしまい，Hiroさんが書かれている部分を引用して書くつもりだったのですが，すっとばしてしまっておかしくなってしまいました．桝岡さんに向けて打ったつもりなので初めのとこは削って，

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ (出だしを削って)速度場と圧力場の関係を 物理的な因果関係とは無関係な，数学的なテクニック としてしまうのは賛成できません．・・・ ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

で，読んでもらえるといいです．私の注意が散漫でした．すいません．

私の立場は『物理における法則を立式化したものはその段階である種の因果が存在するんじゃないのか』というものです． 流体運動に限らず，運動方程式が立った段階で，まずはそこに含まれているパラメータにはある種の因果が成立すると思います．私の場合はあまり難しいことは考慮せず，非圧縮とか極限操作とかは置いといて，たとえば運動方程式に圧力勾配を組み込んだのは，それを研究していたパイオニアが運動と圧力の関係を調べたかったから(かどうかは本人に聞かなければ分かりませんが)であり，そういう意味で因果があるのでは無いのかなぁと言う意味で書きました． さらに例えば，ラプラス方程式を解くにしても物理的な因果から脱却する必要はなくこの操作が

法則(方程式)→運動や力の決定

という新たな因果を作っているようにも思います．これは今ふと思ったことですのでさっきの投稿には書いていませんが．

〉しかし，私は「加速度が発生することによって力が発生する」という「因果」もありだと思っています． #(この感覚は普通だと思っているのですが違うのでしょうか?)

自然な捉え方だと思います．運動方程式の右辺と左辺を入れ替えた結果ですもんね．Hiroさんの意見には賛成です．

桝岡さんが書かれている因果というのが力が先か，速度が先かという話ならばこれ以上首を突っ込むつもりはないですが，もっと違う哲学的なことを指しているのならば今後の研究に参考にさせていただきたいので桝岡さんに是非，お話を聞かせていただきたいのです． 書きながらよく分からなくなってきたんで，私だけ話がずれている感もありますが．．．

物理に因果という言葉を持ち込んだのがまずかったのかもしれないですね． 言葉のアヤがあるのかも？

けん（大学3年） さんのレス (2008/08/22(Fri) 23:22)

＞toorisugari no Hiroさん

流線曲率定理を本で勉強します．ありがとうございました．

桝岡 さんのレス (2008/08/24(Sun) 21:58)

私は，因果関係を，原因と結果の区別(どちらが先か)，と考えて説明していました．

物理現象を数式化すると，数式上では，原因と結果の区別が困難になります． 数式を解くのは，数学的なテクニックであり，計算する順番を変更しても，物理的な原因と結果が変化することはありません． 原因と結果の区別は，物理現象を数式化する過程の，プリミティブな所に戻る必要があります．

物理学は，数式を使って真理を探究する学問であり，相互の関係が明確になれば良く， 物理の専門家にとって，原因と結果の区別は重要では無いかもしれません．

しかし，専門家の ・AからBが決定される． という解説を，非専門家は ・Aが原因でBがその結果である． と解釈する傾向があると感じます． 不正確な物理イメージが広まることを防止するため， 計算手順なのか，原因と結果なのか，区別できるように説明してほしいと思っています．

物理を勉強する上では，原因と結果の区別には，それほど配慮しなくても良さそうですが， 物理現象を数式化した方程式には，物理的な意味があり，数式の物理的解釈は重要だと思います．

圧縮性の流体でも，非圧縮性の流体でも，圧力と速度は相互に影響しています． 非圧縮性の流体では，密度を介さない分，より強く相互に影響しています． 圧力分布を考慮せずに，速度について解けるのは，圧力と無関係に速度が決定されるためではなく， 圧力と速度が強く影響していて，同時に決定されることが，式に組み込まれているためだと思います． ＃解釈の違い，ですね．

mNeji さんのレス (2008/08/24(Sun) 22:37)

横から失礼します．

このスレッドでの桝岡さんのご意見に興味があって，検索したところ ・桝岡さんの紙飛行機のサイトでの解説記事 h ttp://www.aa.isas.ne.jp/v-tails/lift/index.html を興味深く拝見しました．

また，以前に水泳の手の推進力を調べている時に知った， ・飛行の物理的描像：和訳 h ttp://home.comcast.net/~clipper-108/lift-J2.pdf とその出版； ・UNDERSTANDING FLIGHT, David F. Anderson Scott Eberhard， McGraw-Hill Co., ISBN0-07-136377-7. のような説明が，流体一般にも望まれると感じました．

その意味でも； ＞物理現象を数式化した方程式には，物理的な意味があり，数式の物理的解釈は重要だと思います．

これには強く賛同するものです．とは言え，自分は流体力学をまだ克服できないでいるので，大きな事は言えませんが...．でも，数値流体力学が詳しく計算される現代にこそ，流体力学の物理的描像を是非とも明確にして頂きたいと思います．

この場合，必ずしも「因果関係」を追求するという観点に留まらずに，流体力学的特徴を，数式に対応して物理的(モデル)解釈を付けるべきではなかろうかと思います．

傍観者の無責任発言をお許しください．

toorisugari no Hiro さんのレス (2008/08/25(Mon) 16:34)

誤解されているようなので

> 数式を解くのは，数学的なテクニックであり，計算する順番を変更しても，物理的な原因と結果が変化することはありません．

非圧縮流体の速度の決定に関しては「テクニック」や「計算する順番」は関係ありません．「非圧縮性」を仮定した瞬間に「圧力は受動的」になります． # (そうでないのなら，数式で根拠を説明していただけると幸いです．)

「非圧縮性を仮定することが数学的なテクニック」ということなら，受容できます．(そのときは「剛体」も数学的なテクニックになりますが．)

kei さんのレス (2008/08/30(Sat) 20:29)

桝岡さん

私がこれまで書き込んできたことはかなりズレにズレていたようなので忘れてください．

〉私は，因果関係を，原因と結果の区別(どちらが先か)，と考えて説明していました．

私も物理学にとどまらず物事の原因と結果は大切だとは思います．しかし，今回の非圧縮の流体の問題において因果関係を持ち込むのは危険だと思います． 単純な運動方程式は書き方を変えるだけで意味が変わります．つまり

F=ma

とすれば，既知の運動(速度)に追従して力(圧力)が決まるし，

ma=F

とすれば，力にマッチした運動が決定されます． けんさんの初めの書き込みの返信として，既知の圧力に対する速度依存性を述べられたという内容ならば頷けますが，一般論としてのものならばやはり，まずいのではないでしようか？

非圧縮ということは，流体として時間発展の向きを逆にすることは可能ですよね？私は流体における可逆性を知らないのでこの段階で間違えている可能性はありますが，これが正しいのならば，桝岡さんが主張されている原因と結果は逆発展をとることによって逆転してしまうのではないでしようか？ 逆転するということはこの系で原因と結果は同じ土俵に立つことになり，区別することに意味を持たないように思うのですが．

因果という言葉を使っていいのは非可逆な系を論じるときだけだと思うのですがどうでしよう？