分極電荷

分極電荷

メントス(4年) さんの書込 (2008/08/16(Sat) 15:49)

毎度お世話になります． 自分で答えを出してみたのですが，チェックのほうをよろしくお願いします．

問題 半径が，a,b,c,dの同心球を考える．r>aの領域をA,というふうに決めていき，A,B,C,D,Eの領域を考える．(Eはd<rです．)AとCは導体，BとDは誘電率εの誘電体，Eは真空である．始めに全く電荷の存在しない状態から，導体Cに正の電荷Qを与えた．どこにどれだけの分極電荷が生じるか．

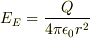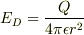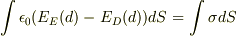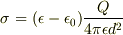答え 電場は，ガウスの法則より， Eで E_{E}=\frac{Q}{4\pi \epsilon_{0} r^{2}} Dで E_{D}=\frac{Q}{4\pi \epsilon r^{2}} Cは導体中なので0 B,Aは電荷が存在しないので0． よって，Dの領域に電場による分極電荷が生じると考えました． r=dのところで表面分極電荷σが生じるとすると，r=dを挟んだ円柱を考えて \int \epsilon_{0}(E_{E}(d)-E_{D}(d))dS=\int \sigma dS よって， \sigma=(\epsilon -\epsilon_{0})\frac{Q}{4\pi\epsilon d^{2}} になると考えました． r=cのところには，-σが出来ると思います． 領域Bの誘電体には，電場がないため分極は生じません．

あっていますでしょうか？

Re: 分極電荷

yama さんのレス (2008/08/16(Sat) 23:25)

σの値を求めたところまでは合っていると思いますが・・・

>r=cのところには，-σが出来ると思います．

これではDの誘電体全体の電荷が0になりません． 外側(r=d)の面と内側(r=c)の面の面積の違いに注意しましょう．

Re: 分極電荷

メントス(4年) さんのレス (2008/08/17(Sun) 01:06)

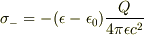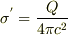凡ミスでした・・・． r=cのところでは， \sigma_{-}=-(\epsilon -\epsilon_{0})\frac{Q}{4\pi\epsilon c^2} が出来ます． あと，導体の領域では，r=cのところに， \sigma^{'}=\frac{Q}{4\pi c^2} の表面電荷が生じていると思いますが，これは真電荷ですから，分極電荷とは言いませんよね？

Re: 分極電荷

yama さんのレス (2008/08/17(Sun) 10:04)

導体の表面電荷は分極電荷とは言えないでしょうね．