抵抗力のある落下運動の問題について
抵抗力のある落下運動の問題について
ユーテー さんの書込 (2008/08/15(Fri) 02:49)
高専4年です.物理学の課題の,
「質量mの物体が速度vに比例する抵抗力-kvを受けつつ落下運動をした結果,時間tで距離y移動した.抵抗係数と質量の比k/mを求めよ.ただし,初期位置0,初速度0,重力加速度をgとする.」
という問題で,k/mを求めるところの途中ででつまづいてしまいました.
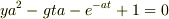 (
( 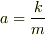 )
上式を"a=_"の形にしたいのですがどうすれば良いかわかりません.求め方が間違っているかも知れないので申し訳ないです.ヒントだけでも教えていただければ幸いです.よろしくお願いいたします.
)
上式を"a=_"の形にしたいのですがどうすれば良いかわかりません.求め方が間違っているかも知れないので申し訳ないです.ヒントだけでも教えていただければ幸いです.よろしくお願いいたします.
Re: 抵抗力のある落下運動の問題について
mNeji さんのレス (2008/08/15(Fri) 12:37)
ユーテーさん,初めまして.
お示しの式は次元に不一致が見られます.一度,運動方程式を示して,得られた解とともに示されないと,どこで困っているのか解り難いと思います.また,座標系の取り方も明確にしておく方が良いですね.
Re: 抵抗力のある落下運動の問題について
ユーテー さんのレス (2008/08/15(Fri) 21:38)
運動方程式は, 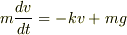 で,これをv(t)について解いたら,
で,これをv(t)について解いたら,
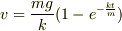 となりました.
ここで,vを時間積分して落下距離y(t)を求めたら,
となりました.
ここで,vを時間積分して落下距離y(t)を求めたら,
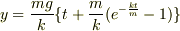 となりました.
y,t,gがわかっているので,それを使って
となりました.
y,t,gがわかっているので,それを使って 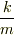 の式に直そうとしているのが初めの質問で聞いているところです.
上手く説明できなくて申し訳ないです..
の式に直そうとしているのが初めの質問で聞いているところです.
上手く説明できなくて申し訳ないです..
Re: 抵抗力のある落下運動の問題について
mNeji さんのレス (2008/08/15(Fri) 23:40)
簡単な問題の時こそ,ケアレス・ミスに注意しましょう.そういう私でさえ,よくするのですが....
垂直軸の下向きにy座標を取ったとすれば,運動方程式は合っていると思います.すると,辺々をmで割ると, 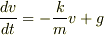 ですね.
ですね.
ここで,定数項 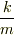 は時間の逆数の次元を持っているので
は時間の逆数の次元を持っているので 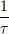 とします.
とします.
とすると,変数分離形にできる;
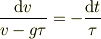
ここで,辺々は無次元であることに注意しましょう.これから先は,ご自分でチェックしてください.
数学の問題だと無次元の場合が多いと思いますが,物理の運動方程式では次元があります.出来るだけ,直感的な常数を定義しておくと,式の変形中に「次元チェック」が出来ます.面倒でも,順番に見返す癖をつけておくと良いと思います.
で,正しい解が出たとして,指数関数部分が線形で無い為に話が複雑になります.そこで,t<τとかt>τとかで場合分けして検討出来ませんか?
Re: 抵抗力のある落下運動の問題について
mNeji さんのレス (2008/08/16(Sat) 08:38)
微分方程式を解かないで,ケアレス・ミスと申し上げました事をお詫びします.問題は,最後まで計算しないといけません:→自分.
さて,本論に戻ります.あるtとyとの組の値が判るという事は,あるtとvとの組の値も判ることですね.同様にdv/dtも判るわけです.とすると,時間をパラメータにして, 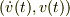 のグラフを書けば,その傾きから
のグラフを書けば,その傾きから 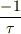 を決めることができます.解析的な方法ではありませんが....
を決めることができます.解析的な方法ではありませんが....
Re: 抵抗力のある落下運動の問題について
ユーテー さんのレス (2008/08/16(Sat) 17:01)
こんなにめんどくさい問題だったとは...後は自力でやってみます. 返答ありがとうございました.
Re: 抵抗力のある落下運動の問題について
なんとなく さんのレス (2008/08/16(Sat) 18:39)
横レス失礼.
お気づきかも知れませんが,この問題ではt→∞での漸近的な挙動でいいのでないですか.指数項は速やかに0に近づきます.
Re: 抵抗力のある落下運動の問題について
toorisugari no Hiro さんのレス (2008/08/16(Sat) 19:19)
主題者の意図を考えると,たぶん,陰的な表示式
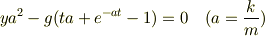
で解答としては十分だと思います.
どうしても,その先に進みたければ 上の式を無次元化したもの
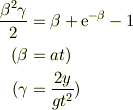
を考えます.ただし,文中には明記されていませんが, 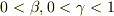 です.
です. 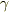 をパラメータに
をパラメータに 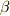 の挙動を調べるという問題ですね.
の挙動を調べるという問題ですね.
特に 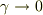 ,
,  の両極限,あるいはおなじ事ですが,
の両極限,あるいはおなじ事ですが,  ,
,  の両極限,は計算が簡単になるので,これを調べればだいたいの挙動はわかるのでは?
の両極限,は計算が簡単になるので,これを調べればだいたいの挙動はわかるのでは?
# なんとなくさんがおっしゃっているのは  (
( 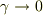 )の場合ですね.
)の場合ですね.