ラグランジュ方程式と変分
ラグランジュ方程式と変分
digi さんの書込 (2008/08/13(Wed) 16:58)
ラグランジュ方程式を変分を使って導出する方法がありますよね?
物理量 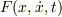 について,
について,
![I[x]=\int_{t_1}^{t_2}F(x,\dot{x},t)dt \\I'[x']=\int_{t_1}^{t_2}F(x',\dot{x'},t)dt](http://hooktail.maxwell.jp/bbslog/2e5a2a0b19ceb0ea4ff9af37fb2e14ab.png)
(ただし, 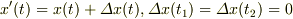 )
と定義する.変分
)
と定義する.変分 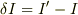 は,
は, 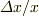 の2次の項以上は非常に小さいとして無視すると,
の2次の項以上は非常に小さいとして無視すると,
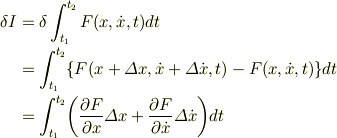
↑は参考書の内容です.
ここでわからないことがあって,2行目から3行目への変形はどのようにしたのでしょうか?「 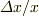 の2次の項以上は非常に小さいとして無視すると」というのがよくわからないのですが.
の2次の項以上は非常に小さいとして無視すると」というのがよくわからないのですが.
Re: ラグランジュ方程式と変分
toorisugari no Hiro さんのレス (2008/08/16(Sat) 18:43)
> 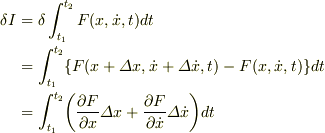
> ここでわからないことがあって,2行目から3行目への変形はどのようにしたのでしょうか?「 |11a4f043370cf0306be561772cba4b3b| の2次の項以上は非常に小さいとして無視すると」というのがよくわからないのですが.
テーラー展開をご存じですか?
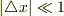 として,
として, 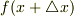 を
を 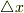 の2次多項式(ただし,係数に
の2次多項式(ただし,係数に 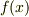 およびその微分を含む)で近似できますか?
およびその微分を含む)で近似できますか?
Re: ラグランジュ方程式と変分
mNeji さんのレス (2008/08/17(Sun) 14:59)
digiさん,横から失礼します.
変分は微分と少し感じが違うという意味で,
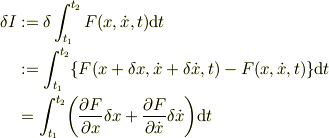
とするほうが自然な気もします.
また,昔,この式を見た時に, 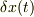 と
と 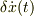 が,あたかも独立変数のように振舞うのが,しっくり来なかった事を思い出しました.かなり紆余曲折して,
が,あたかも独立変数のように振舞うのが,しっくり来なかった事を思い出しました.かなり紆余曲折して,
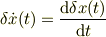
であるのに気づくことになったと記憶しています(苦笑).
だから,面倒でも,
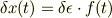
ここで 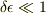 は正の微小常数で,
は正の微小常数で, 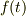 は変分,合わせて微小変分とでも言った方が,紛れないと感じています.
は変分,合わせて微小変分とでも言った方が,紛れないと感じています.
細かなお話で,失礼しました.
Re: ラグランジュ方程式と変分
digi さんのレス (2008/08/17(Sun) 22:30)
mNejiさん,書き込みありがとうございます.
私も, 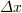 は
は 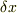 としたほうがいいのかと気になっていました.
としたほうがいいのかと気になっていました.  は微小変化を表すものと思っていいのでしょうか?でも,
は微小変化を表すものと思っていいのでしょうか?でも, 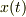 は普通の関数だから,微小変化を表すのは
は普通の関数だから,微小変化を表すのは 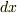 とか
とか 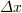 でもいいのではないでしょうか?
でもいいのではないでしょうか?
Re: ラグランジュ方程式と変分
mNeji さんのレス (2008/08/17(Sun) 23:05)
>私も, 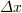 は
は 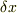 としたほうがいいのかと気になっていました.
としたほうがいいのかと気になっていました.  は微小変化を表すものと思っていいのでしょうか?でも,
は微小変化を表すものと思っていいのでしょうか?でも, 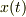 は普通の関数だから,微小変化を表すのは
は普通の関数だから,微小変化を表すのは 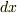 とか
とか 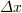 でもいいのではないでしょうか?
でもいいのではないでしょうか?
私は,数学に弱いので厳密な定義は知りませんが,ある関数G(x)を考えたとき,その微分 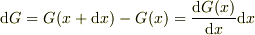 は関数が微分可能であれば,一意的に決まりますね.
は関数が微分可能であれば,一意的に決まりますね.
ところが,経路積分に於ける変分は,ある意味,恣意的に本来の解から「適当にずらすのであって,かつその量は微量な変化」です.ですから,微分操作のように一意的でないですね.ただし変分の場合,始点と終点での値がゼロという束縛条件はありますね.
ですから,微分操作ないしは偏微分操作と変分操作は,常に交換可能であるとおもいます(数学的に証明している訳では有りません).逆に言えば,「 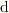 ,
, 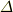 」や「
」や「 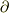 」などと「
」などと「  」とは区別したいと思います.
」とは区別したいと思います.
Re: ラグランジュ方程式と変分
digi さんのレス (2008/08/17(Sun) 23:56)
わかりました.mNejiさん,どうもありがとうございます.
Re: ラグランジュ方程式と変分
toorisugari no Hiro さんのレス (2008/08/18(Mon) 14:50)
> わかりました.mNejiさん,どうもありがとうございます.
えっと,最初の疑問は解消されたのでしょうか?
念のため,続きを.
> |f9a4147118084194e12c3b998f0a65c9| のテイラー展開ですが, > |779e169560c1bb862ef2f668aab67f63|
今度は 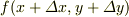 を
を 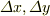 の一次式で近似してみてください.上の結果を利用すればできるはずです.
の一次式で近似してみてください.上の結果を利用すればできるはずです.
Re: ラグランジュ方程式と変分
digi さんのレス (2008/08/19(Tue) 00:51)
>えっと,最初の疑問は解消されたのでしょうか?
まだです.お返事ありがとうございます.
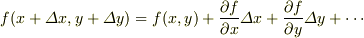
これで2次以降の項を無視すればいいということですか?
 の
の  ,
, 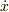 は
は  の関数ですが,同じような展開でいいのでしょうか?
あと,変分を考える場合は
の関数ですが,同じような展開でいいのでしょうか?
あと,変分を考える場合は 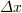 よりも
よりも 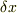 としたほうがいいでしょうか?
としたほうがいいでしょうか?
Re: ラグランジュ方程式と変分
toorisugari no Hiro さんのレス (2008/08/19(Tue) 12:30)
>  の
の  ,
, 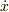 は
は  の関数ですが,同じような展開でいいのでしょうか?
の関数ですが,同じような展開でいいのでしょうか?
そうです.
独立な変数 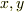 に対する関数
に対する関数 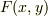 を変分した
を変分した 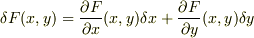 に
に 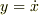 を代入すると考えます.
を代入すると考えます.
> あと,変分を考える場合は |cbb30cc8b6a55491070906dbe199478a| よりも |58b1e9f4b9a86690cb106e65a265a34f| としたほうがいいでしょうか?
統一性があればどちらでもかまいませんが,普通  で記述するので,それに倣う方がいいでしょう.
で記述するので,それに倣う方がいいでしょう.
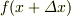 のテイラー展開ですが,
のテイラー展開ですが,
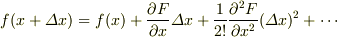 でいいでしょうか?
でいいでしょうか?