けみ さんの書込 (2008/08/11(Mon) 00:17)

はじめまして． けみと名乗っている高３です．

流体力学では気体も液体も同じ"流体"として扱いますよね．そうやって総称できるのは，様々な面で両者が同じ，あるいは似た性質を示すからだと思います． しかし，分子レベルで見ると，両者の様子は随分違います．

そこで２点質問なのですが， ｉ）分子運動レベルで考えたとき，その全体を流体と呼べる条件は何ですか．つまり，流体と呼べるものがもつ，分子運動の特徴は何ですか． ii）分子レベルで，粘性なとが現れる仕組みは，気体と液体で違いますか． よろしくお願いします．

toorisugari no Hiro さんのレス (2008/08/11(Mon) 09:39)

けみさん この疑問はどのような背景から出たのですか?学校などの課題ですか?入試問題ではなさそうですが．．．

けみ さんのレス (2008/08/11(Mon) 17:14)

Toorisugari no Hiroさん

特に課題とかそういったものではなく，ふとした疑問です． 元々，流体力学の範疇で，空気中のボールの運動を考えていました．それで，粘性抵抗や慣性抵抗を考えているうちに，どういう仕組みになっているのか気になりはじめました．結局は分子運動に還元できるはずだと．その時に，気体と液体を総称して流体と呼ぶ，流体力学の前提がとても不思議に思えて，ここに書き込んだ，という経緯です．

両者に何か共通点があるからまとめている，のではなく，両者を流体と規定した上であらゆる流体に共通する性質を調べるのが流体力学だ，ということなんでしょうか，，，

toorisugari no Hiro さんのレス (2008/08/11(Mon) 17:59)

けみさん，本当に高校3年生ですか? :-)

> 粘性抵抗や慣性抵抗を考えているうちに，どういう仕組みになっているのか気になりはじめました．結局は分子運動に還元できるはずだと．

# 高校生の範疇越えています．:-)

> 流体力学では気体も液体も同じ"流体"として扱いますよね．そうやって総称できるのは，様々な面で両者が同じ，あるいは似た性質を示すからだと思います．

弾性体等の固体と流体はともに連続体ですが，弾性体と流体の違いは前者は変形に対して復元力が働くのに対して，流体は一旦変形してしまえば，もとに戻ろうとはしない，ということです．

つまり，(体積を変えないような)変形に対して復元力が発生しない連続体を流体と呼びます．

通常，液体や気体が流体になりますが，等号ではありません．

(雪は固体ですが，雪崩の時はほぼ流体と考えられます．車の流れを流体として捉える見方もあります．)

> 分子運動レベルで考えたとき，その全体を流体と呼べる条件は何ですか．

「流体」とは巨視的(マクロ)な性質です．微視的(ミクロ)に分子だけをみて，流体かどうかは判定できません．それに，粒子の集合，粒子群(離散的)と連続体は相反する概念です．

そもそも，一部の分子の振るまいを(短時間)観ただけで，固体かそうでないか判定はできません．粒子数や体積を無限にしたときに(熱力学的極限)，固体，液体という「相」は意味を持ちます．

それとも，粒子群を連続体近似できる条件という意味でしょうか? それなら，平均自由行程より大きな長さスケールの運動を観るとき，粒子群は連続体，つまり流体と見なせます．

流体とはマクロに見たときに現れる性質なのです．

> 分子レベルで，粘性なとが現れる仕組みは，気体と液体で違いますか．

流体は変形をいやがりませんが，素速い変形，すなわち，変形速度，をいやがるかは自由です．素速い変形をいやがる性質を「粘性」と呼び，変形速度に対する応答係数を「粘性率」と呼びます．粘性率が高いと，ゆっくりとしか変形できません．変形を起こそうとしている者からは「抵抗」が発生しているようにみえます．

見方を変えると，粘性とは運動量を隣接する流体へ「輸送」する現象です．あるいは速度の平均化と言い換えても良いです(ここら辺は理解できなくて良いです) ．ここに分子の運動が絡んできます．また，気体と液体では粘性なとが現れる仕組みは異なります．詳しくは

• http://www.chemistryquestion.jp/situmon/shitumon_kurashi_kagaku52_fluid_viscosity.html

を見てください．

mNeji さんのレス (2008/08/16(Sat) 12:14)

けみさん，初めまして．

昨日のTVで，不思議な物質の映像がでました．3m程度の広がりをもつ水槽に特殊な溶液が入っていて，その上を人が走り抜けようとすると，ゆらゆらしながら進めました．ところがゆっくりと歩くと，ズブズブと沈んでしまいましたが，その人の脇を他の人が走って行くのはとても興味深いものでした．

人間の時間スケールの中で，弾性体的な振る舞いと液体的な振る舞いとを目視できるのですから愉快ですね．その特殊な溶液とは「水とカタクリ粉を等量に混ぜたもの」とか言っていたような気がします．

kei さんのレス (2008/08/18(Mon) 10:10)

けみさん

高校生でここまでのことを考えることができるけみさんには未来の物理の世界を引っ張っていってもらいたいです．toorisugari no Hiroさんがすばらしい答えを提示されているので書き込もうか迷ったんですが少し難しい気がしたので補足という形で．

流体力学というのは名のごとく“流れ”を研究する分野です．もし粒子が100個あってそれらが全て同じ方向に運動すれば，粒子100個の運動は“流れ”をなすといえるでしよう．toorisugari no Hiroさんが粒子群と書かれているのはこういうことだと思います． しかしながら，粒子のすべてが全て完全に相似な運動をするわけではありません． i番目の粒子を取り出した時の速度viは，100個の粒子の平均速度<v>と，各々の粒子が持つ熱的(ランダム)な振動速度vriを用いて

vi = <v> + vri

と表現できます．流れと呼ばれるものは100個の粒子がすべて持っている平均速度<v>が形成するであろうとみなせますよね？こいつが同じ方向に運動するという情報を担っているわけです． vriが存在するために1個の粒子に注目するとジグザグ運動をしますが，この値がランダムなので，全体をみる(マクロにみる)と全粒子間で打ち消しあって大きな流れとなっているわけです．条件を書けと言われると，少なくとも

vri/<v>→1よりもかなり小さい値

と書けないといけませんね．要するに個々の振る舞いが無視できるくらい流れの速度(フローということもありますが)がでかくないと流体とは言えません． 流体とは粒子1つ1つの個性を殺した表現ともいえます．

では熱運動vrが流体運動に無関係かというとそうではなく，実はこれが粘性の性質を生み出しています．ある粒子は熱運動を持ち隣の粒子と相互作用をもつようになります．結果toorisugari no Hiroさんが書かれている“輸送”現象が生じ，観察すると我々のいうところの粘性が生まれるということです．

高3生ということで時間が取れないかもしれませんが，もし式の展開などに興味があるようなら本屋さん，あるいは図書館で

非平衡の統計力学

という分野に絞って資料を集められることをお勧めします．

できるだけ式を使わず説明してみましたが式を使って説明できるなら，流体力学に出てくるナビエ‐ストークスの式と上で述べた式が同じ形になるために流体とみなしていいじゃないか，という一言につきてしまいます．

toorisugari no Hiro さんのレス (2008/08/18(Mon) 14:24)

keiさん，followありがとうございます．

一つ気になったので．

> vri/<v>→1よりもかなり小さい値

でなくて

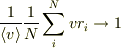「 よりもかなり小さい値」 ですよね．

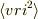は音速(の2乗)に相当するので，どの平均を取るのか気になったので．

kei さんのレス (2008/08/18(Mon) 15:23)

toorisugari no Hiroさん

><vri^2>は音速(の2乗)に相当するので，どの平均を取るのか気になったので．

<>は普通の平均です．Hiroさんも提案してくださったものの中に書かれている

<vri> = 1/N×?vri

です．足した数で割り算する小学校一番最初に習うやつです．ただ足し方が違って何回も同じ実験をしてそのたびにi番目の粒子を追跡して，その実験回数で平均をとっており，粒子数で平均をとっているわけではないです． 分布関数を重みとしてかけた統計平均

<vri> = ∫ vri f dv

と言ったほうがわかりやすいかもしれないです．

音速になるかどうかは浅学なので分からないですが，Hiroさんの提示されたものの方が私のものよりも厳密でいいですね．粒子全体を考慮できていますし．訂正ありがとうございます．

私のオリジナルの条件に意味をつけるなら，あくまで各要素一つ一つの粒子のあるサンプル(実験)についてそれが流れを構成する要素としてふさわしいかを評価するものだと思ってもらえればOKです．

また，Hiroさんが訂正してくださったものは，粒子1つ1つでなく，全体を見渡した時にメインのフローとすべての粒子が作り出した流れの乱れを評価したものだと理解すればよいでしようか．

けみさんには条件のあたりにはそれほど拘らずに，そんなもんなんだ〜と思っていただければ良いでしよう．数年後に修行をつんだ，けみさんにあのときの書き込みはここがおかしいかったと突っ込んでもらえると書き込んだかいがあったかなぁ〜と思えます(笑)