ジャンプする剛体棒

home > 掲示板 >

このページのPDF版

サイトマップ

ジャンプする剛体棒

メントス(4年) さんの書込 (2008/08/09(Sat) 18:55)

試験の過去問からです．図がなくて，分かりづらかったらすみません．

長さl，質量Mの一様な棒が水面上に置かれ，その両端にジャンプ力発生装置が取り付けられている．二つのジャンプ力発生装置は同じもので，それぞれ重さが無視できるコイルと質量mの鉄心から成り，コイルに通電すると鉄心がコイルにひきつけられて運動量を得て，一体になるようになっている．この撃力によってジャンプが起こる． 1，棒の右端を回転軸としたときのジャンプ力発生装置を含む棒全体の慣性モーメントを求めよ．

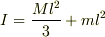
答え $I=\frac{Ml^{2}}{3}+ml^{2}$

2，棒の左端に通電し，初速度の大きさvで飛び上がった．棒の左端が達する最高点の高さを求めよ．(Iの記号は使ってよいそうです．)

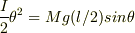
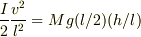
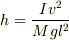
答え右端まわりのエネルギー保存則から $\frac{I}{2}\theta^{2}=Mg(l/2)sin\theta$ $\frac{I}{2}\frac{v^{2}}{l^{2}}=Mg(l/2)(h/l)$ $h=\frac{Iv^{2}}{Mgl^{2}}$

3，棒の左端が最高点に達したときに棒の右端のジャンプ力発生装置に通電したところ，右端はすべることなく飛び上がった．このときの重心の初速度の大きさをV，重心回りの角速度ωを求めよ．ただし，通電してから右側がジャンプを開始するまでの時間内においては，左端は最高点にとどまっているものとする．また，このときの棒と水平面のなす角は十分小さい．

重心に関する量を求めなければならないので，重心回りのエネルギー保存を立てるのかと思いましたが，飛び上がる瞬間の情報しかないので，保存則が立てられません．重心回りの角速度は，滑らない条件，また右端のジャンプ力発生装置は左端と同じものということから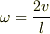， $\omega=\frac{2v}{l}$ でしょうか？

よろしくお願いします．

Re: ジャンプする剛体棒

yama さんのレス (2008/08/09(Sat) 21:20)

合っています．

2. 間違っています．ジャンプ力発生装置を含む棒全体の質量が M+2m であることに注意しましょう．

3. 間違っています． 2.の場合は右端を軸として回転しますが，3.の場合は左端が自由に動けるので，左端を軸とする回転にはなりません．重心の運動と，重心のまわりの回転に分けて考えるといいでしょう．また，発生する撃力の力積は2.の場合と同じであると考えられます．

Re: ジャンプする剛体棒

メントス(4年) さんのレス (2008/08/10(Sun) 19:04)

2番は 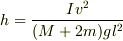$h=\frac{Iv^{2}}{(M+2m)gl^{2}}$ でした．

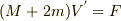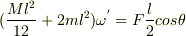
3番ですが，ジャンプ装置による力をFとすると重心の運動方程式は $(M+2m)V^{'}=F$ 重心回りの回転運動方程式は $(\frac{Ml^{2}}{12}+2ml^{2})\omega^{'}=F\frac{l}{2}cos\theta$

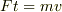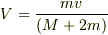
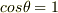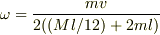であり，また，運動量と撃力の関係は Ft=mv なので $V=\frac{mv}{(M+2m)}$ $cos\theta=1$ と近似して $\omega=\frac{mv}{2((Ml/12)+2ml)}$ となりました．どうでしょうか？

Re: ジャンプする剛体棒

yama さんのレス (2008/08/10(Sun) 23:30)

回転運動方程式の左辺の慣性モーメントが間違っているようです．２個の鉄心の重心のまわりの慣性モーメントは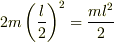， $2m\left(\frac{l}{2}\right)^2=\frac{ml^2}{2}$ です．

運動量と撃力の関係が 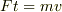Ft=mv というのもおかしいと思います．は，鉄心と棒が一体となったときの左端の速度です．

Re: ジャンプする剛体棒

メントス(4年) さんのレス (2008/08/11(Mon) 15:42)

慣性モーメントはミスでした．すみません．

撃力の部分が分からないのですが，ジャンプ装置は左，右とも同じものですから得られる撃力も同じmvなのではないのですか？

Re: ジャンプする剛体棒

yama さんのレス (2008/08/11(Mon) 20:43)

質量mの鉄心が速さvで棒に衝突するわけではありません．衝突する速さはvより大きいはずです．衝突後に棒と一体となって動くときの左端の速さがvです．

Re: ジャンプする剛体棒

メントス(4年) さんのレス (2008/08/12(Tue) 15:00)

すみませんが，もう少しヒントを頂けませんか？

Re: ジャンプする剛体棒

yama さんのレス (2008/08/12(Tue) 23:27)

左端に撃力Fがはたらくときの棒の回転の運動方程式は次のようになります．

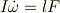
$I\dot\omega=lF$

撃力は瞬間的にはたらく大きい力なので，重力は無視しています．初めの角速度を0として，運動方程式を積分すると

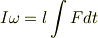
$I\omega=l\int Fdt$

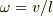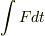となります． $\omega$ は撃力がはたらいたあとの棒の回転の角速度です．すなわち $\omega=v/l$ です．これから力積 $\int Fdt$ が求められます．

Re: ジャンプする剛体棒

メントス(4年) さんのレス (2008/08/13(Wed) 00:35)

ありがとうございます．重心速度は 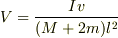$V=\frac{Iv}{(M+2m)l^{2}}$ 重心回りの角速度は 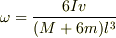$\omega=\frac{6Iv}{(M+6m)l^{3}}$ となりました．

問題とは直接関係ないのですが，問題文に書かれている「右端がすべらなく飛び上がった」条件から重心速度＝右端の速度，になると思うのですけれど，上の答えを利用して 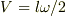$V=l\omega/2$ を計算してみると，Mの係数が一致しないです．まだ，どこかに間違いがあるのでしょうか？

Re: ジャンプする剛体棒

メントス(4年) さんのレス (2008/08/13(Wed) 17:41)

もしかして，自分は物凄い初歩的な勘違いをしてるのかもしれません．剛体のところでよく出てくる拘束条件，すべらないときは，重心の速度＝表面での速度というのは，転がる円のみについて成り立つものなのでしょうか．棒の場合はどうなのでしょう？

Re: ジャンプする剛体棒

yama さんのレス (2008/08/13(Wed) 20:57)

棒は転がるのではなく，飛び上がるわけです．同時に重心を中心とする回転も生じるので，重心の速度と右端の速度が異なるのは当然です．

「重心の速度＝表面の速度」という場合の表面の速度というのは重心の静止系における速度です．また，滑らずに転がる円でも，例えば曲面上を転がる場合には「重心の速度＝表面での速度」にはなりません．

Re: ジャンプする剛体棒

メントス(4年) さんのレス (2008/08/13(Wed) 22:58)

＞棒は転がるのではなく，飛び上がるわけです．ぜんぜん関係ありませんでした．すみません．

この問題は解決しましたが，剛体に関しての自分の理解がかなり曖昧だったようで心配になってきたので，いくつか確認をさせていただけないでしょうか？話がズレてしまって，大変申し訳ありません．

1，まず，剛体に関する速度と角速度の関係について・固定軸あり→P点での速度＝固定軸からP点までの距離×角速度・固定軸なし→P点での速度＝重心軸からP点までの距離×角速度これは間違っていないでしょうか？

2，すべりの条件について教科書をみても，あまり詳しく書いていないので，今までなんとなく使っていたのですが，すべりの条件はどういったときに成り立つのでしょうか？＞「重心の速度＝表面の速度」という場合の表面の速度というのは重心の静止系に＞おける速度です．というのは，重心の移動速度＝他の物体との接触点の速度あるいは，床が静止しているときならば重心からみた接触点の速度＝0 ということですよね？タイヤが平面な床を運動しているときに，これが物理的に「滑らない」ということを意味しているのは理解できます．

例えば，棒が鉛直な壁と水平な地面に接していて，壁からの抗力，重力，床からの抗力を受けて壁に沿って滑り落ちていく場合はどうなるのでしょうか．壁と棒はθの角度をなしています．私の持っている問題集だと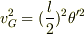， $v_{G}^{2}=(\frac{l}{2})^{2}\theta'^{2}$ が成り立つと書いてあります．この問題では，棒に固定軸はないので，1番の考えから右辺は重心からみた床との接触点の速度だろうと思います．ということは，この式は，重心速度＝接触点速度の滑らない条件なのでしょうか？

＞また，滑らずに転がる円でも，例えば曲面上を転がる場合には「重心の速度＝表面での速度」にはなりません．どういうことなのでしょうか？？

ご迷惑をおかけして，すみません．

Re: ジャンプする剛体棒

yama さんのレス (2008/08/14(Thu) 01:02)

一般に剛体の一点Pの速度は次のようになります．

$\bm v=\bm V+\bm\omega\times\bm r$

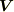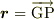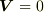ただし， $\bm V$ は剛体の任意の点Gの速度で， $\bm r=\overrightarrow{\mathrm{GP}}$ です．多くの場合，Gを重心にとると都合がよいのですが，重心でなくてもかまいません． Gが固定点の場合は，当然 $\bm V=0$ です．

滑らない条件は，接触点における相対速度が0であることです．相対速度が0でなければ滑ることになります．

>例えば，棒が鉛直な壁と水平な地面に接していて，壁からの抗力，重力，床からの抗力を受けて壁に沿って滑り落ちていく場合はどうなるのでしょうか．

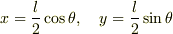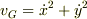この場合は壁に対しても床に対しても棒は滑っているので，滑らない条件というのは成り立っていません．問題集の式は，重心の座標を $x=\frac{l}{2}\cos\theta,\quad y=\frac{l}{2}\sin\theta$ として $v_G=\dot x^2+\dot y^2$ を計算することによって導かれます．

>＞また，滑らずに転がる円でも，例えば曲面上を転がる場合には「重心の速度＝表面での速度」にはなりません． >どういうことなのでしょうか？？

これは私の勘違いだったようで，曲面上を転がる場合にも成り立つようです．

Re: ジャンプする剛体棒

メントスさんのレス (2008/08/15(Fri) 02:08)

＞多くの場合，Gを重心にとると都合がよいのですが，重心でなくてもかまいません．重心じゃなくても良いのですか？モーメントの釣り合いのときは，軸の取り方は任意でしたが，運動するときは，固定軸があるならば，固定軸．ないときは重心に軸を取るものだと思っていました．本質的に，剛体は重心を軸にして運動をするのではないのですか？(よく，猫が壁から飛び降りるときに，重心を軸にして回転するなんて話を聞きます．)

＞問題集の式は，重心の座標をとしてを計算することによって導かれます．滑らない条件は関係なかったのですね．拘束条件は問題によって，その都度，考えなければならないと理解しました．

Re: ジャンプする剛体棒

yama さんのレス (2008/08/16(Sat) 02:25)

多くの場合，重心は簡単な運動をするので，重心の運動と，そのまわりの回転運動に分けて考えのが都合がよいわけです．例えば力がはたらかないときは重心は等速直線運動をするし，一様な重力場がある場合は重心は等加速度運動をします．しかし，重心以外の点はこのような単純な運動はしないので，重心以外の点を基準にとると，計算がややこしくなります．それでもかまわなければ，重心以外の点を基準にとることができます．

Re: ジャンプする剛体棒

メントスさんのレス (2008/08/16(Sat) 12:11)

よくわかりました．ありがとうございました．

[home] [掲示板] [ページの先頭]