極座標変換
極座標変換
digi さんの書込 (2008/08/06(Wed) 02:46)
任意のベクトル(Ax, Ay, Az)(デカルト座標表示)を極座標表示(Ar, Aθ, Aφ)に変換するにはどうすればいいのでしょうか?2次元なら図を書けばわかるのですが3次元の場合は図が描きにくいです.計算でできるのでしょうか?
Re: 極座標変換
toorisugari no Hiro さんのレス (2008/08/06(Wed) 03:05)
- 位置ベクトルを極座標系で記述します.
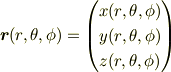
- 極座標系における正規直交基底を以下の手順で求めます.
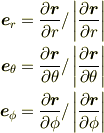
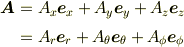
を利用して
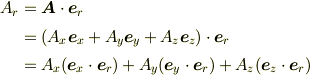
となるので,各内積を計算すれば 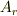 が求まる.
が求まる. 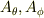 も同様.
も同様.
Re: 極座標変換
digi さんのレス (2008/08/06(Wed) 23:26)
お返事ありがとうございます.
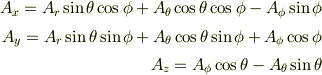
と求まりました.それで速度ベクトルと加速度ベクトルの極座標表示を求めようと思い, 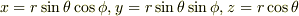 をそれぞれ1回,2回微分してそれを上で求めたAx,Ay,Azの形と比較しました.
をそれぞれ1回,2回微分してそれを上で求めたAx,Ay,Azの形と比較しました.
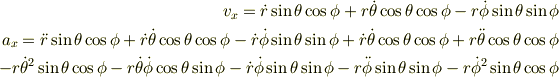
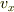 と
と 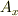 との比較から
との比較から 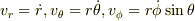 が得られ,これは参考書と同じになったのですが,加速度のほうがうまくいきません.参考書では
が得られ,これは参考書と同じになったのですが,加速度のほうがうまくいきません.参考書では 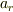 に
に 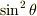 の項が含まれるのですが,上の
の項が含まれるのですが,上の 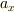 と
と 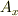 の比較からは出てこないような気がします.どこか間違っているのでしょうか(参考書では別の求め方が載っているのですが,この方法ではだめなのでしょうか)?
の比較からは出てこないような気がします.どこか間違っているのでしょうか(参考書では別の求め方が載っているのですが,この方法ではだめなのでしょうか)?
Re: 極座標変換
toorisugari no Hiro さんのレス (2008/08/07(Thu) 00:35)
> 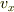 と
と 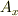 との比較から
との比較から
無精せずに全成分を計算して,内積を計算すべきです.
# 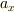 の最後の項が抜けていますね.
の最後の項が抜けていますね.
# 私なら 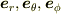 の微分を
の微分を 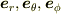 で表す計算をしてから,
で表す計算をしてから,  を微分します.
を微分します.
Re: 極座標変換
digi さんのレス (2008/08/07(Thu) 15:58)
の最後の項が抜けてました.ご指摘ありがとうございます.
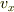 と
と 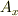 の比較から
の比較から 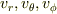 は求まるのに,
は求まるのに, 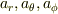 が求まらないのはなぜなのでしょうか?その理由が知りたいです.間違いがあればご指摘お願いします.
が求まらないのはなぜなのでしょうか?その理由が知りたいです.間違いがあればご指摘お願いします.
Re: 極座標変換
toorisugari no Hiro さんのレス (2008/08/07(Thu) 20:02)
> その理由が知りたいです.
ベクトル全体で考えるべき所を  成分だけで考えているからです.
成分だけで考えているからです.  がうまくいったのは「偶然」です.
がうまくいったのは「偶然」です.
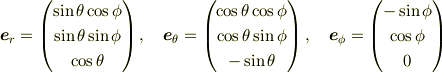
として
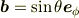
の微分を考えます.
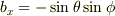 を微分して
を微分して 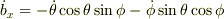 ですから
ですから
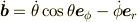
としたくなります.
しかし, 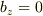 より,
より, 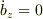 ですが,上の
ですが,上の  成分の値は0ではありません.
成分の値は0ではありません.
この矛盾の原因は, 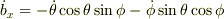 の最後の項を,本当は
の最後の項を,本当は 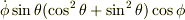 が正しいのに,そのまま
が正しいのに,そのまま 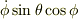 と観たからです.他の成分も見ないと判断できないのに,
と観たからです.他の成分も見ないと判断できないのに,  成分だけで後者と判断したのが間違いの元です.
成分だけで後者と判断したのが間違いの元です.
(正解は
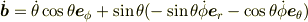
です.)