guta さんの書込 (2008/08/05(Tue) 21:03)

ジャイロスコープの歳差運動についてなのですが，ファインマン物理学に「運動が落ち着いてきたときには・・・（20-3）」という段落があって，おやと思いました． 軸を水平に抑えておいて，その後離したらジャイロスコープは歳差運動（反時計回りとする）をし，次第に歳差軸まわりの回転が減速し，鉛直軸周りのトルクが無くなる．すると軸が始めのいちよりも低くなって角運動量ベクトルの向きが下へ傾く．すると角運動量が鉛直成分を持つので鉛直軸周りにトルクが生じる． とここまでを自分なりに理解したのですが，この生じたトルクは実際鉛直下向きになって，初めの回転の向きとは逆向きになってしまい，これでは文章中の「その軸をわずかに下げることによって，鉛直軸周りの回転が維持される」ことにならなくなってしまいます． わかりにくい書き方ですが，どうか助言の方，よろしくお願いいたします．

mNeji さんのレス (2008/08/06(Wed) 06:43)

gutaさん，初めまして．

論点が良く判らないのですが．例えば，重力下にある通常のコマがある一点で支えられて歳差運動をしている時に，その支点に摩擦力が有る様な時の問題を考えようとしているのですか？

guta さんのレス (2008/08/06(Wed) 07:51)

mNejiさん，はじめまして．返信ありがとうございます． 大学一年のgutaです．

わかりにくい書き込みで申し訳ございません．

具体的には『ファインマン物理学力学』の20-3（pp.282-283の「運動が落ちついたときには〜」より）を読んでてわからないところがありました．

自分で問題になったのは，中心に枢軸を通した円輪の歳差運動であり，mNejiさんの言うコマでも同じモデルになれるかと思います．（ただしコマの軸を水平にして回転できることにしてください） そこで問題になっている状況は「完全に軸を水平に保っておいて急に手を離したとする」場面です．本によるとその後「軸の位置がはじめよりも少し低くなっている．」とあります． そこでわからなかったのは，「軸が低くなるので回転の角運動量も小さい鉛直成分を持つようになるのであり，それがまさに歳差運動のために必要だったものである」，「軸をわずかに下げることによって鉛直軸の周りの回転が維持される」という記述です．これはどうしてなのでしょうか．

返信よろしくお願いします．

mNeji さんのレス (2008/08/06(Wed) 11:22)

＞『ファインマン物理学力学』の20-3（pp.282-283の「運動が落ちついたときには〜」より）を読んで

私も，一年生のときにはファインマンさんの本に傾倒していましたが，理解出来ずに，夏休みの終わりころに撤退しました．

さて，手元に『ファインマン物理学力学』がないので状況がわかりません．絵を書き易くする為に，球体の中心に棒が刺さったモデル，「──●─」とします．棒の質量は無視できて，球の中心がコマの重心に一致するとします．すると歳差運動が起こる状況は； <pre> +z軸 │ │ │ │ │ ／ │／ │●G │ ／ │／ │／ │／ O ・───────────────── +y

/

/

+x

</pre>

原点Oでコマの一方は滑らかに拘束されているとします．コマは，O→Gに向いた時に角速度ωで右ネジ方向に回転するとします．従って，その角運動量は慣性能率Iとして；

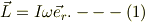
ここで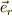， は，O→Gに向いた単位ベクタとします．

重力はz軸の負の方向を向いているとしますと，原点以外にコマに働く外力は；

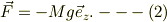
従って，角運動量の方程式は；

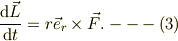
ここで， は，O→Gの長さとします．

と書きましたが，外積などを使ってはいけないとか...．そもそも，角運動量の式は使えましたか？

mNeji さんのレス (2008/08/06(Wed) 15:36)

＞「軸が低くなるので回転の角運動量も小さい鉛直成分を持つようになるのであり，それがまさに歳差運動のために必要だったものである」， ＞「軸をわずかに下げることによって鉛直軸の周りの回転が維持される」

情けない事には，この歳になってもチンプンカンプンです，ご免なさい．

でも，しかし，見方を換えると「問題」の部分だけでも判れば，少しは解釈出来るかも知れませんね．

guta さんのレス (2008/08/06(Wed) 22:09)

ご検討ありがとうございます． 数式はすべて理解できます．これは大丈夫です． ちなみに問題は支点Oの支えを外した瞬間後の状況です． すると軸の端（原点にない方）がサイクロイドの運動を波打つようにしてだんだんと減速して下がっていくらしいです．

＞「軸が低くなるので回転の角運動量も小さい鉛直成分を持つようになるのであり，それがまさに歳差運動のために必要だったものである」， ＞「軸をわずかに下げることによって鉛直軸の周りの回転が維持される」 ＞でも，しかし，見方を換えると「問題」の部分だけでも判れば，少しは解釈出来るかも知れませんね．

そうなんです！「問題」がどうにもわからなくて，，． はじめz軸の正方向に歳差運動の角速度ベクトルが向いているとしたら，減速して軸が傾き，r方向のベクトルが低く傾き，Lベクトルが傾き，それによってdL/dt=・・・のしきによりトルクがまた生じるんですが，そのトルクの向きが不都合なことに始めz軸まわりに回転していた方向と逆のモーメントを生じさせるものになってしまい，，，，「問題」とつじつまがあわないんです．

mNeji さんのレス (2008/08/07(Thu) 00:12)

＞ちなみに問題は支点Oの支えを外した瞬間後の状況です．

ああ，これなら検討の余地がありますね．言うならば前回書いて置いた，Oxyz座標のOxy平面のなかで歳差運動している最中に，原点の束縛を外す訳ですね．歳差運動由来の重心の運動速度と角運動量とを初期条件にして，自由な角運動量が重力下で，どのような落下の振る舞いをするかを考えるのでしょうね．

＃大雑把には，重心の自由落下と，重心を中心にした「コマの軸中心の角運動量」と「初期条件(それまでの歳差運動)の回転運動」との重ね合わせのような感じがします．←ちょっと変ですね． ＃直ぐには解けそうにないので，急がれる場合は，他の識者の方にヘルプを出されると良いと思います．

＞そうなんです！「問題」がどうにもわからなくて，，．

いっその事，原本をご覧になると判りよかったりしませんか？

mNeji さんのレス (2008/08/07(Thu) 01:33)

まだ少ししか判りませんが，原点の拘束を解除する寸前の様子を考えます．簡単のために，重心Gがx軸の正の方向を向いた時とします．

●図1xz平面● <pre>

z ｜ ｜ Mge_z｜ ↑｜ G L=Iωe_x

O・────●── ── x

↓-Mge_z </pre>

歳差運動をしている時に，原点Oでは，コマ全体が落下しないので，Gにかかる重力と逆の力が抗力として働いている．原点での拘束を解除する時には，瞬間的に，その逆の力，-(Mge_z)を加えると考える．

すなわち，束縛を解除する一寸に，重心系から似て-(Mge_z)を加わり，重心からにた歳差運動が短時間に発生して止まる．この一時的に発生する歳差運動の方向は，それまでの歳差運動の方向と逆と思われます，何となく．

この先はまだ未定．

他方，角速度の運動方程式を整理すると；

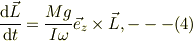
重心の歳差角速度が；

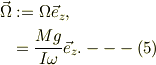
従って，重心の回転速度；

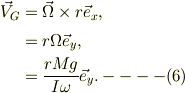
図示すると； ●図2xy平面● <pre>

y ｜ ｜ ｜ V_G=rΩe_y

｜ ↑ L=Iωe_x

O・────●── ── x

</pre>

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/08(Fri) 12:49)

ｇｕｔａさんこんにちは ｋｏｍａｇａｔａｋｅです． 横から失礼します．

ファインマンの本を持っていましたので見ながら考えてみました． まだきちんと計算できているわけではありません． 推測です．

図の２０−２にジャイロの説明があります． 先にこれに従って考えて見ます．

角運動量Ｌ０で回転しているジャイロの回転軸の方向（ｙ軸の方向）をｚ軸の方向に回そうとすると新たにｘ軸周りの回転が生じます．この角運動量をΩとしています． こういう変化を起こすために必要なトルクはτ＝Ω×Ｌ０です（積はベクトル積です）．トルクの方向はΩの方向とＬ０の方向に垂直です．ｘ軸とｙ軸に垂直ですからｚ軸の方向です．トルクがｚ軸の方向を向いているということは偶力がｘｙ面内になければいけないことになります．（これは素朴な力のイメージとはかなり食い違うものです．普通は傾けたい方向に力を加えます．）

これを踏まえて，独楽の場合と横になって回転しているジャイロの場合を考えています．

図２０−３で独楽の才差運動を取り上げています．偶力は重心に働く重力から出てきます．重力は独楽を倒す方向に働いているのに倒れないのはどうしてだろうかという問いに対する答えです． トルクは水平面内接線方向です．回転軸の変化により発生する新たな回転の角運動量Ωの方向は独楽の回転軸とトルクとに垂直です．Ω，Ｌ，τの順で右ネジになっていますからオメガの方向は才差運動の回転軸に交差する方向です．才差運動の回転の角運動量はΩの鉛直成分になるのだろうと思います． （図２０−４はわかりにくいです．独楽の位置をｚ軸に対して右側に書くとトルクは右ネジの進む方向で紙面を貫く方向です．新たな回転は独楽を向こう側に倒すような方向になりますから才差が起こります． 図２０−１では回転台の上に立っている人が描かれています．本文では椅子に座っているとなっています．ちょっと食い違いがありますね．）

図の２０−５はジャイロを支えて回転させている時に支えている手を離したらという場合のことです．これも手を離すと下に落ちるはずなのにどうして落ちないのだろうかという問いに対する答えになります．

Ｏ−−−Ｇ−−−Ｐ

初めＰで支えていました．ジャイロの重心がＧです．角運動量ＬはＯＰの方向です．Ｐでの支えを外します．Ｇにかかっている重力によるトルクが発生します．トルクの方向はＯＰに垂直で水平面内です．新たに生じる回転による角運動量Ωの方向はトルクとＬに垂直ですからｚ軸です．ジャイロはｚ軸周りに回転し始めるという事になります．独楽の場合と同じことが起こります．

でもこれは定性的な話です． 重力による重心の落下とｚ軸周りの回転の両方が起こるのですから運動方程式を解いて調べる必要があります．でもファインマンはやっていません． Ｌ０の大きさは変わりません（Ｌ０を変えるようなトルクは働いてはいません）のでｚ軸周りの回転が生じるためには回転のエネルギーが別に必要です．これは重力の位置エネルギーからしか出てきません．必要なエネルギーはｚ軸周りの慣性モーメントと角速度から(1/2)Ｉω^2のはずです． 少し重心が下がった状態でｚ軸周りを回転しているはずだということになります．

独楽の場合も初めの鉛直面内の回転から才差運動に移るところを考えると傾くことによって重心が下がりその位置エネルギーで才差の回転のエネルギーをまかなっているというのは成り立っているはずです．図の２０−３では初めから才差運動があったとしたらでスタートしていますから見えてこないのです．

運動の最初にサイクロイドを描くというのは運動方程式を解かないとわからないことだろうと思います． これがわかる方がおられましたらお願いします．

現在の理解の程度はこれくらいです．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/08/08(Fri) 22:04)

ｇｕｔａさん

追加です．

＞軸を水平に抑えておいて，その後離したらジャイロスコープは歳差運動（反時計回りとする）をし，次第に歳差軸まわりの回転が減速し，鉛直軸周りのトルクが無くなる．すると軸が始めのいちよりも低くなって角運動量ベクトルの向きが下へ傾く．すると角運動量が鉛直成分を持つので鉛直軸周りにトルクが生じる．

これは私が書いたことと違う理解ですね．才差運動が減速するという話はないと思います．手を離したときから下に下がるのです．安定した回転になるとサイクロイドが消えて少し先が下がった回転運動になっているということです．

＞「軸が低くなるので回転の角運動量も小さい鉛直成分を持つようになるのであり，それがまさに歳差運動のために必要だったものである」，

（これについては推測でしか答えることができいません．） ここで言っている回転の角運動量はもともとのジャイロのものです．頭が下がりますから鉛直軸方向の成分は下向きになっています．これが上向きの才差の角運動量を打ち消すのです．元々鉛直軸周りの角運動量＝０だったのですから新たに上向きの角運動量が生じたら別に下向きの角運動量が生じて打ち消しているはずだということを言っているのだろうと思います．

こう考えるとこまの場合でも同じことが言えそうです． 独楽は傾くことで才差運動が生じます．傾くと角運動量の鉛直方向成分が減少します．この分が才差運動の角運動量になっているはずです．

少し重心が下がるというのはエネルギー保存と角運動量の保存という２つの要請を満たすものになっているということになります．

mNeji さんのレス (2008/08/09(Sat) 08:55)

gutaさん，中間報告です．

私の説明には幾つかの落とし穴があるようです．取り敢えず，先にお書きした説明は忘れてください．

大雑把にいって，

（２）角運動量の重心廻りの回転と重心の回転とが混在する様になっている． （１）慣性能率が球対称となる；慣性能率テンソルの対角成分だけで，すべて等しい場合でないといけない．

と思われます．とくに慣性能率テンソルの扱いが出来ないので，しばらくは論議を進められません．

中途半端な意見を書いて，混乱を引き起こした事をお詫びします．これに懲りずに，本を丁寧に解釈されるのをお続けくださると良いと思います．

guta さんのレス (2008/08/09(Sat) 10:29)

mNejiさん，komogatakeさん，綿密な検討ありがとうございました．完全かはわかりませんが，理解を深めることができました． komogatakeさんの， 「・・・ｚ軸周りの回転が生じるためには回転のエネルギーが別に必要です．これは重力の位置エネルギーからしか出てきません．必要なエネルギーはｚ軸周りの慣性モーメントと角速度から(1/2)ＩΩ^2のはずです． 少し重心が下がった状態でｚ軸周りを回転しているはずだということになります． 」 「ここで言っている回転の角運動量はもともとのジャイロのものです．頭が下がりますから鉛直軸方向の成分は下向きになっています．これが上向きの才差の角運動量を打ち消すのです．元々鉛直軸周りの角運動量＝０だったのですから新たに上向きの角運動量が生じたら別に下向きの角運動量が生じて打ち消しているはずだということを言っているのだろうと思います．」 という回答で，私の中では一応すっきりいったつもりですし，（わざわざファインマンを見てくださってありがとうございます．またわたしの誤解のご指摘も感謝しております．）

mNejiさんの支えを放した瞬間の考え方，丁寧な図による報告にも感謝しています． ファインマンは原本も読んでます．（翻訳は図書館で借りてます．）ここの部分は両者とも割りと簡素な記述だったので，助言を求めさせていただきました．今後とも努力し続けたいと思います．ありがとうございました．

mNeji さんのレス (2008/08/10(Sun) 14:17)

ちょっとした情報ですが；

下記の本；

書名 力学−新しい視点にたって− 著者名 Ｖ．Ｄ．バージャー共著Ｍ．Ｇ．オルソン共著戸田盛和共訳田上由紀子共訳 出版社 東京培風館

の「角運動量の解説」は評判が良い様です．

この掲示版のプロジェクトでも，クロメルさんが記事を書きかけになっているようですが，続きを書いて戴けると面白そうですね．

私は，簡単な思考実験を検討していて，自分の頭が，どこに納得がいかないかを探しています．上の図書を予約中なので，来たら自分の不満点が解決するかを楽しみにしています．

また，図書館の新書紹介リストで見ただけですが；

書名 力学１（現象と数学的体系から見える物理学１） 著者名 平尾淳一共著岸根順一郎共著牧野哲共著師啓二共著徳永旻共著 出版社 東京森北出版 ＩＳＢＮ 9784627158115

も，従来の説明から少し違った印象を持ちました．

以上，ご参考まで．