鈴 さんの書込 (2008/08/03(Sun) 12:24)

初めまして．大学一年の鈴といいます． 大学の問題で分からない事があったのでよかったら教えて下さい．

問題 質量M，半径R,中心軸周りの慣性モーメントIの滑車の両側にひもをたらして，左端と右端にそれぞれ質量ｍ１，ｍ２（ｍ１＞ｍ２）のおもりをつるして静かに放した．滑車の支持軸周りの回転は滑らかで，ひもは伸び縮みせず質量を無視できるとする．

（１）片方のおもりが床面に達して後，もう一方のおもりが滑車の支持具に引っ掛かり，そこで止まった．このときの回転角速度をω ，おもりと滑車の間の運動摩擦係数をμ とするとき，滑車が止まるまでの回転角を求めよ．ただし，ひもの摩擦力を無視する．

まず，慣性モーメントを使って滑車の回転角速度を求めるということをしましたが，支持具に引っかかるというところから，どのように考えればいいか分からなくなりました． どのような順序でといていけばいいのでしょうか？ よろしくお願いします．

mNeji さんのレス (2008/08/03(Sun) 20:33)

鈴さん，初めまして．

むしろ，「片方のおもりが床面に達して後のもう一方のおもり」の運動方程式がどう書けるかが重要ですね．一度書いて見られたらどうですか？

#一度，糸が切れたとして考えたのですが，それでは行けない様ですね．

もう一方のおもりの衝突点は，そのおもりが滑車の右端にぶつかる点と仮定したら如何でしょうか．

mNeji さんのレス (2008/08/04(Mon) 05:03)

逆に教えて戴きたいのですが，

（１）m1が床に着く前には，糸と滑車は「滑り」無しで運動しているのでしょうか？

（２）m1が床に接したあと，少なくとも糸の左端には重力は作用出来ませんが，どうして，滑車と糸との間に摩擦力が生じるのでしょうか？

mNeji さんのレス (2008/08/04(Mon) 23:32)

私は，この問題を「糸と滑車との動摩擦係数をμ」として計算してしまいました(笑)．意外と面白いもんですね．

さて「（１）片方のおもりが床面に達して後，」以下は，その前問とは独立に考える事ができます．すなわち，

質量M，半径R,中心軸周りの慣性モーメントIの滑車が角速度ωで回転している時に，質量m2のおもりを，滑車の頂上の位置に置いてた．ただし左右方向には固定されているが，上下方向にはおもりの自重m2gが掛かっているだけである．またおもりと滑車の間の運動摩擦係数をμ とするとき，滑車が止まるまでの回転角を求めよ．ただし，ひもの摩擦力を無視する．

とすれば，滑車の角運動量の式を考えれば良いだけですね．

鈴 さんのレス (2008/08/05(Tue) 17:52)

mNejiさん 返信ありがとうございます．

角運動量の式を使って解いてみました． 角速度を出すために，dL/dt=R*μmgを積分して， L=(R*μmg)*t を出しました． このとき方に自信はないのですが， このあとどうやって回転角を求めればいいのでしょうか？

教えていただけるとうれしいです． よろしくお願いします．

mNeji さんのレス (2008/08/05(Tue) 23:00)

滑車の中心を座標原点Oとし，右方向にx軸，垂直上方にy軸，手前にz軸とすると，O xyz系は右手座標となります．

おもりは，(x,y,z)=(0,R,0)に静止して，滑車はt＝０の時にzの正な点から見て，半時計方向に回転し，その角速度はωと与えられています．滑車の回転角度を，t＝０の時に，y軸から見てθとするとします．とすると，滑車の角運動量はz軸方向の成分しか無く，それをLとすれば，

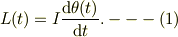
初期条件は，

角運動量の時間変化は，外部からのトルクにより生じますから，

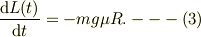
(1)を(3)に代入して整理すれば，

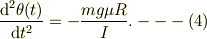
此れを初期条件(2)のもと，積分すれば良いのでは？