量子力学
量子力学
apple さんの書込 (2008/07/31(Thu) 23:08)
(問題) 自由空間(真空中)を質量m,電荷‐e(e>0)を持った電子が一定速度vで運動する場合,この電子のもつ波長は,ド・ブローイの量子条件λ=h/pより与えられる.ここで,pは運動量,hはプランク定数である.電子の波長λと運動エネルギーEの関係を式で表せ.
(自分の考え) E=(1/2)mv^2=p^2/2m λ=h/pより E=h^2/2mλ^2
となったのですが,これでは間違っているらしいです. なぜこれではいけないのでしょうか?? (粒子性と波動性をごっちゃにしているのがいけないのかな・・・)
回答よろしくお願いします.
Re: 量子力学
mNeji さんのレス (2008/08/01(Fri) 00:10)
appleさん,初めまして.
前期量子論の場合では運動量pは演算子でないので,ご提示された,
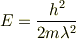
でも間違えではないと思います.
ただ,電磁気などの波動では,例えば,x軸に進行している波を波数k,振動の角振動数ωで表す;
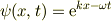
と書く事が多いので,波長  より,
より,
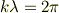
の関係から,波数で表す事が多いとおもいます.従って,
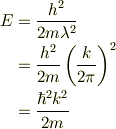
ここで, 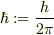 で,しばし「エイチ・バー」と読まれます.
で,しばし「エイチ・バー」と読まれます.
私見ですが,分子にくるパラメータの方が,直感的だからだと思います.
Re: 量子力学
apple さんのレス (2008/08/01(Fri) 00:33)
mNejiさん,回答ありがとうございます.
ずっと前から,気になっていることがあるのですが,E=ch/λを式変形しても,上の式になりませんが,どうしてでしょうか?
Re: 量子力学
なんとなく さんのレス (2008/08/01(Fri) 11:50)
横レス失礼します.
mNejiさんが仰っていますが,p=ch/λは光子(電磁波)の波長と運動量の関係式です.ド・ブロイ波長は物質(粒子)の波動性を仮定したものですが,物質とは(静止)質量が0でないという特徴があります.相対論ではエネルギーEは E^2=c^2p^2+m^2c^4 の関係があるため,(光子などの)質量0(の素粒子)ではE=cp=ch/λです. 逆に物質粒子ではm≠0のために,全エネルギーは通常は運動量pに比較して,質量の効果がずば抜けて大きく(言い換えれば速度v<<c),運動エネルギー部分の近似式, E=p^2/2m が使えます. もし,答えが間違いであるというなら,運動量の(特殊)相対論的な表示 p=vE/c^2 を使えということかも知れませんね.大雑把に言えばvが光速の10%くらいになると,相対論的効果が無視できなくなると思います. 蛇足ですが,電子の速度は容易く,そのくらいになります.
Re: 量子力学
mNeji さんのレス (2008/08/02(Sat) 00:37)
もう納得された様ですが,光子について少し変形して見ましょう.
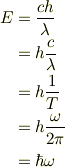
光子エネルギーの角振動数表示といった所ですかね.エネルギーが高くなると  も大きくなりますね.
も大きくなりますね.
Re: 量子力学
yama さんのレス (2008/08/02(Sat) 00:56)
横から失礼します.
エネルギーと振動数の関係 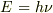 および運動量と波長の関係
および運動量と波長の関係 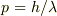 は,光子についても電子についても共通に成り立ちます.
しかし,速度との関係を考える場合は,粒子の速度と波の速度を区別する必要がありますし,波の速度にも2種類あることに注意する必要があります.
は,光子についても電子についても共通に成り立ちます.
しかし,速度との関係を考える場合は,粒子の速度と波の速度を区別する必要がありますし,波の速度にも2種類あることに注意する必要があります.
上記の関係式を,角振動数 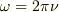 と波数
と波数 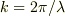 を用いて表すと次のようになります.
を用いて表すと次のようになります.
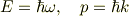
波面の移動速度を位相速度といい, 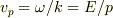 です.
波束の移動速度を群速度といい,
です.
波束の移動速度を群速度といい, 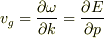 です.
です.
光の場合は 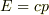 なので
なので 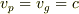 となり,位相速度と群速度が一致します.
となり,位相速度と群速度が一致します.
電子の場合は 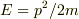 なので
なので
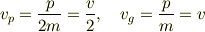
となります, すなわち電子波の群速度は粒子の速度に一致しますが,位相速度は粒子の速度の半分になるわけです.
光について成り立つ関係式 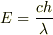 に相当する式は,電子の場合は
に相当する式は,電子の場合は 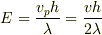 になります.
になります.
Re: 量子力学
mNeji さんのレス (2008/08/02(Sat) 09:50)
yamaさん,
>すなわち電子波の群速度は粒子の速度に一致しますが,位相速度は粒子の速度の半分になるわけです.
「群速度は位相速度よりも常に低い」とばかり思っていました.この問題に触れている本をご存知でしたら,お教え下さいませんか?
Re: 量子力学
yama さんのレス (2008/08/02(Sat) 20:36)
砂川重信「量子力学」に簡単な説明があります.
Re: 量子力学
mNeji さんのレス (2008/08/02(Sat) 21:15)
>砂川重信「量子力学」に簡単な説明があります.
理論電磁気は丁寧に勉強しので,電磁気の発想で量子力学を眺めていました.当時,量子力学は出版されていなかったと思います.もし出ていたら,もう少し量子力学が判っただろうと思います.
絶版の上に,中古も無い様です.区や都の図書館を探して見ます.
ご教示,有り難うございました.
Re: 量子力学
mNeji さんのレス (2008/08/03(Sun) 11:52)
>>砂川重信「量子力学」
が直ぐに見る事が出来ないので,インターネットで検索して見たところ,下記の資料が見つかりました;
・物体の速度と物質波の速度
丁寧な解説と思います.ご参考まで.
頭の固い自分には,まだ納得しがたい点もありますが....